3. Обернена матриця. Обчислення оберненої матриці елементарними перетвореннями

Будемо розглядати квадратні матриці порядку n

А= .

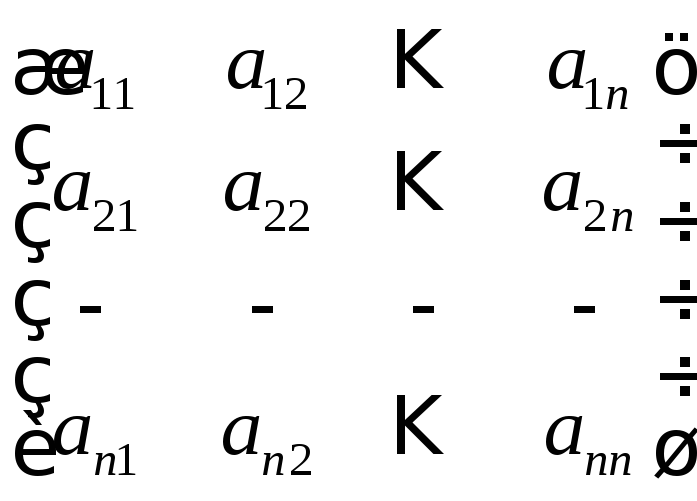Кожний рядок і кожний стовпець матриці А вважатимемо вектором простору . Таким чином, з матрицею А можна зв`язати дві системи векторів :

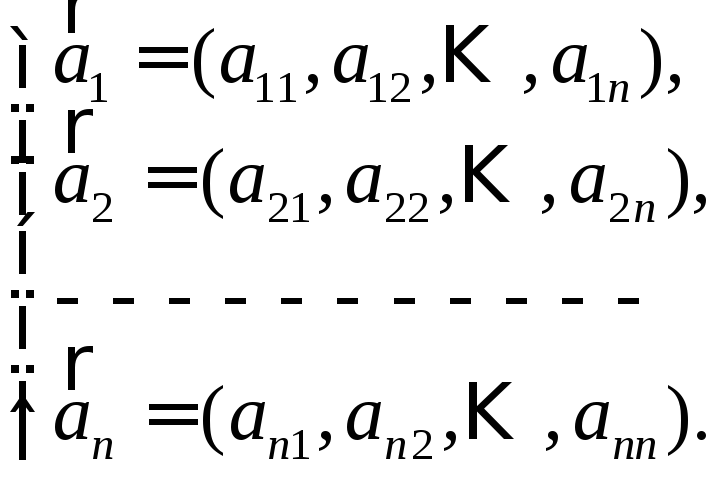(4)

і

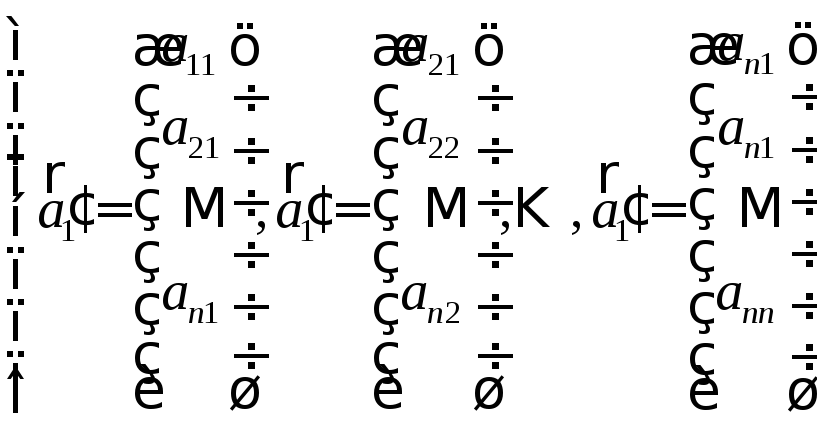. (5)

(4) – система векторів-рядків, (5) – система векторів-стовпців.

Ранг системи (4) дорівнює максимальному числу лінійно незалежних рядків (рядковий ранг матриці А). Аналогічно визначається стовпцевий ранг матриці А. Далі буде доведено, що вони співпадають. Тому їх називають просто рангом матриці.

Означення 5.

Квадратна матрицяn-го порядку називається не виродженою (або неособливою), якщо ранг її векторів-рядків дорівнює n. В противному випадку вона – вироджена (особлива).

Іншими словами, матриця А називається не виродженою, якщо система її векторів-рядків лінійно незалежна.

Означення 6.

Матриця В називається оберненою для матриці А, якщо виконується рівність АВ = ВА = Е.

Позначимо В = , тоді матимемо А=А = Е.

Обернену матрицю може мати лише квадратна не вироджена матриця. Нульова матриця 0 не має оберненої, оскільки для будь-якої матриці В даного порядку 0В = В0 = 0.

Лема 1..

Якщо С = АВ і між рядками матриці А існує лінійна залежність, то точно така ж залежність існує між рядками матриці С.

► Припустимо, що між рядками матриці А існує залежність, тобто виконується рівність

, (6)

де - деякі числа, не рівні одночасно нулю. Доведемо, що така ж рівність справедлива для рядків матриці С, тобто, що

. (7)

Візьмемо довільний стовпець матриці В. Помножимо (6) на вектор

Звідси Або.

Отже, при кожному j=1,2,…,n маємо рівність

. (8)

А це означає, що справедлива рівність (7).

Дійсно, Тому

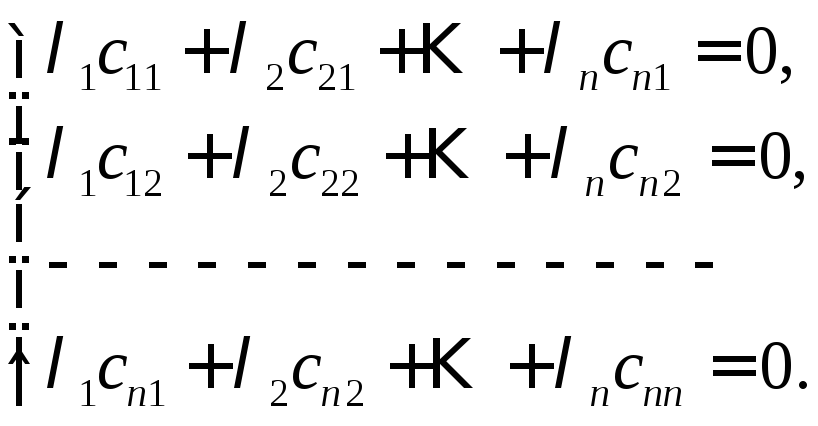(9)

тобто виконується рівність (7). ◄

Теорема 1.

Для особливості матриці А не існує оберненої.

► Припустимо, що для матриці А існує обернена матриця В. Тому виконується рівність АВ = Е. Оскільки за умовою матриця А особлива, то її рядки лінійно залежні. В силу леми 1 така ж залежність повинна бути і між рядками матриці Е. Але це неможливо, бо рядками матриці Е є одиничні вектори, які, як відомо, лінійно незалежні.

Одержане протиріччя показує, що для особливої матриці А обернена не існує.

Теорема 2.

Будь-яку неособливу матрицю А за допомогою елементарних рядкових перетворень можна привести до одиничної матриці.

Навпаки, якщо деяка матриця А приводиться до матриці Е при допомозі рядкових перетворень, то ця матриця неособлива.

► Нехай маємо неособливу матрицю А розміру .

А= .

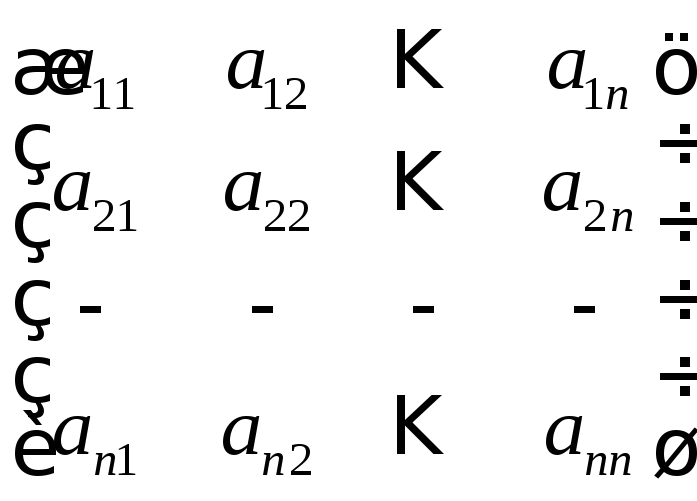В цій матриці не може бути нульового стовпця, бо тоді б ранг матриці А був би менший за n, що протирічить умові (матриця А неособлива). Переставляючи рядки, можна домогтись того, щоб . Помноживши тоді перший рядок на число, ми перетворимов одиницю. Потім при допомозі декількох рядкових перетворень всі інші елементи першого стовпця перетворимо в нулі. В результаті дістанемо матрицю.

,

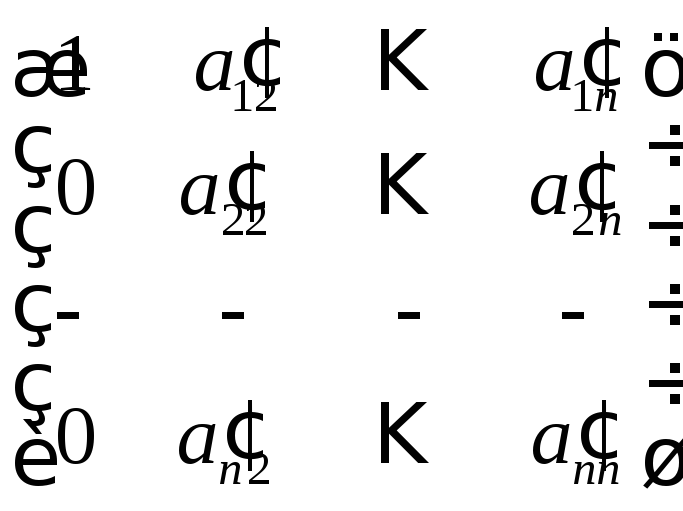Яка буде неособливою в силу не особливості матриці А. Дійсно, кожне елементарне перетворення не змінює ранг матриці і тому переводить неособливу матрицю в неособливу.

Розглянемо в матриці під матрицю, обведену пунктирною лінією. Оскільки і вона є неособливою (лінійна залежність між рядками цієї матриці означала б лінійну залежність між рядками матриці А), то хоч один із елементів її першого стовпця відмінний від нуля.

Переставляючи рядки матриці , домагаємось щоб(перший рядок уже не чіпаємо). Далі перетворюємов одиницю, а всі інші елементи другого стовпця – в нулі. В результаті отримуємо матрицювигляду :

.

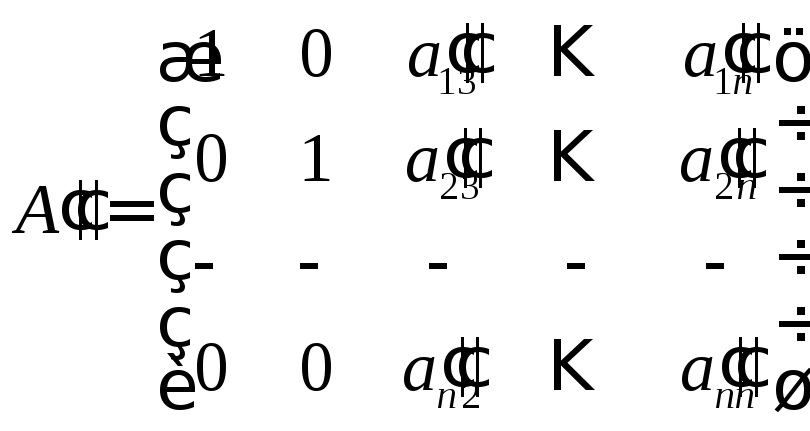І так далі. Після n коренів дістанемо одиничну матрицю Е.

Навпаки, нехай матриця А при допомозі рядкових перетворень приведена до одиничної матриці Е. Оскільки елементарні рядкові перетворення не змінюють ранг матриці, то ранг А дорівнює рангу Е, тобто n. Це означає, що матриця А неособлива. ◄

Наслідок.

Кожну не вироджену матрицю елементарними перетвореннями стовпців можна перетворити в одиничну матрицю.

Має місце таке твердження:

Будь-яке рядкове перетворення матриці А рівносильне множенню цієї матриці зліва на деяку допоміжну матрицю (типу ,чи).

В цьому можна переконатися безпосередньою перевіркою.

Розглянемо матриці ,,.

В матриці всі елементи дорівнюють нулю за виняткомn–2 елементів на головній діагоналі і ще двох елементів за діагоналлю.

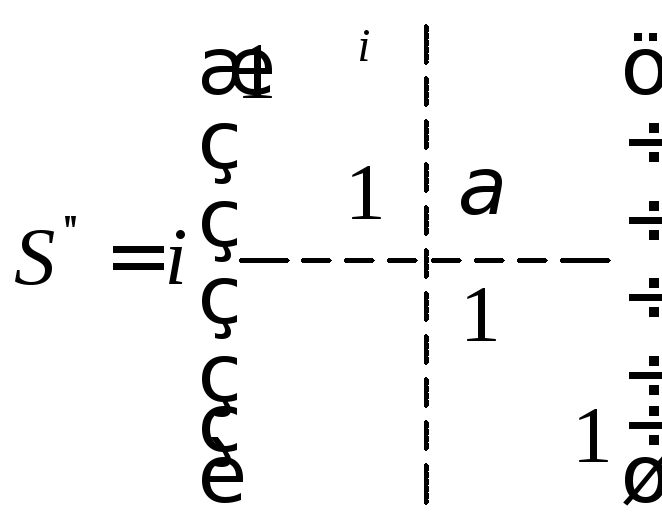
В матриці всі елементи дорівнюють 1, крім одного, який дорівнює, а інші елементи – нулі.

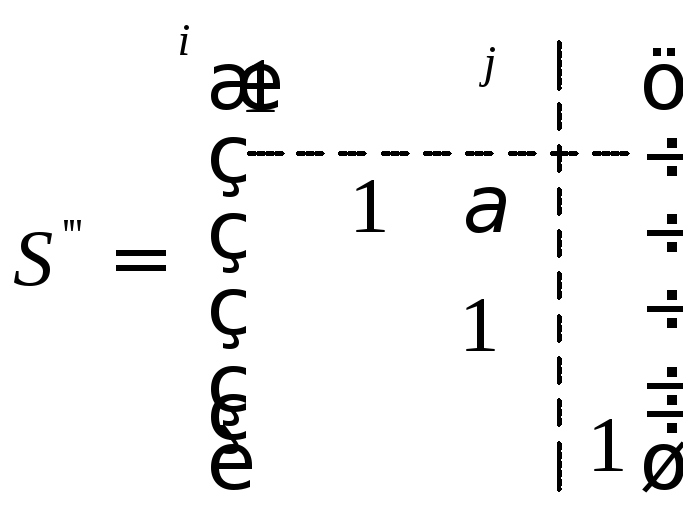
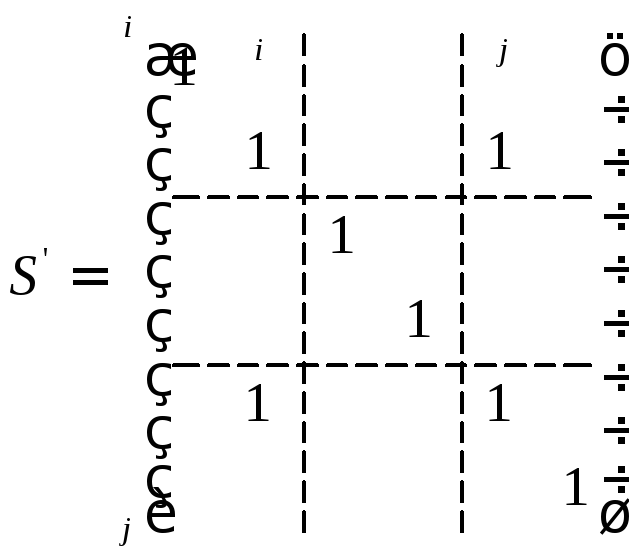
В матриці всі елементи дорівнюють 1, є ще елемент, інші елементи нулі.

Матрицю А дістаємо з матриці А перестановкою в нійі-го і j-го рядків;

Матрицю А дістаємо А множеннямі-го рядка на число ;

Матрицю А дістаємо з матриці А додаванням доі-го рядка j-го рядка, помноженного на .

Враховуючі цей результат, з теореми 2 отримуємо наслідок.

Якщо неособливу матрицю А помножити зліва послідовно на деякі матриці, то дістанемо одиничну матрицю Е :

. (10)

Тут - матриці типу,,, які відповідають рядковим перетворенням матриці А, які приводять її до одиничної. ОскількиА = Е, то з рівності (10) виплаває, що

= . (11)

Помножимо обидві частини рівності (11) на матрицю Е, отримаємо

= Е.

Отже, якщо до матриці Е застосувати той же ланцюжок рядкових перетворень, при допомозі яких матриця А зводиться до Е, то отримаємо матрицю .

Будь-яке стовпцеві перетворення матриці А рівносильне множенню цієї матриці справа на деяку матрицю (типу ,,). Для перетворень стовпців міркування аналогічні.

В результаті сформулюємо такі правила:

1. Для знаходження матриці, оберненої до квадратної матриціn-го порядку А, необхідно прямокутну матрицю розміруза допомогою елементарних перетворень рядків звести до вигляду. Одержане при цьому матриця С є оберненою для матриці А.

2. Для знаходження матриці треба прямокутну матрицюрозміруза допомогою елементарних перетворень стовпців звести до вигляду. Одержана при цьому матриця С буде оберненою до матриці А.

Приклад.

Знайти матрицю , обернену до матриці

.

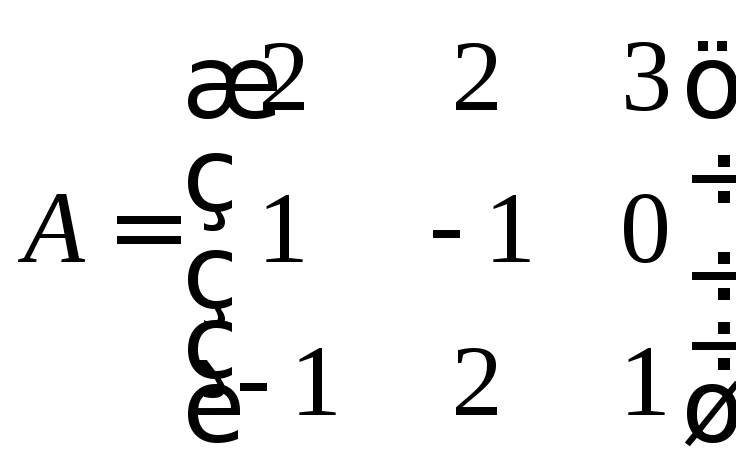Матриця А не вироджена, оскільки ранг її векторів рядків дорівнює трьом. Отже, матриця існує.

Запишемо прямокутну матрицю

.

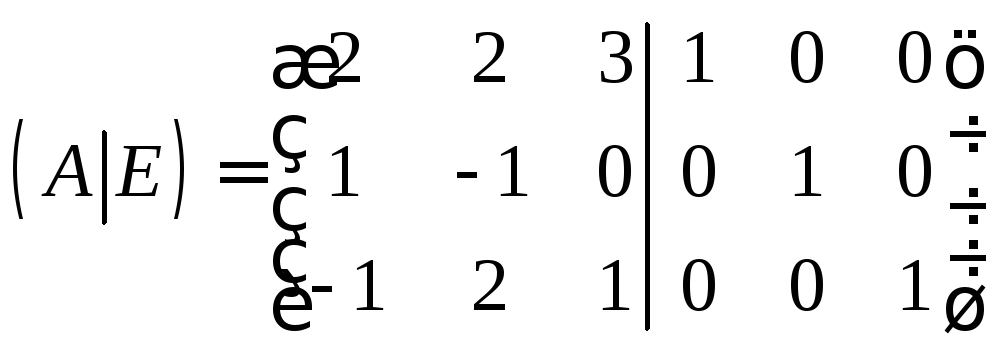За допомогою елементарних перетворень рядків зведемо цю матрицю до вигляду :

.

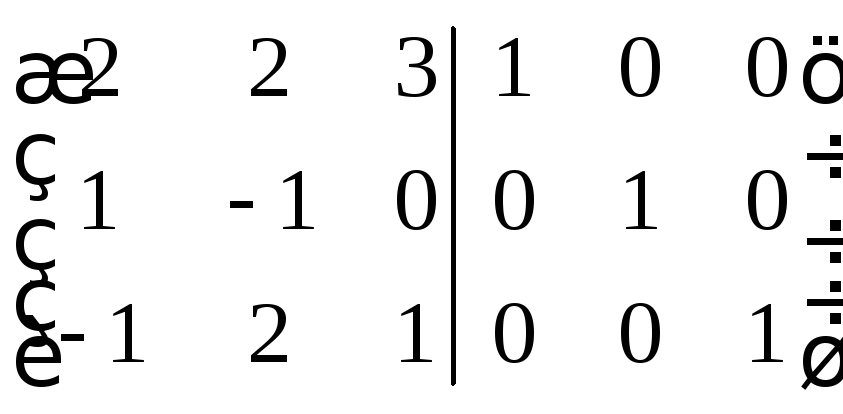
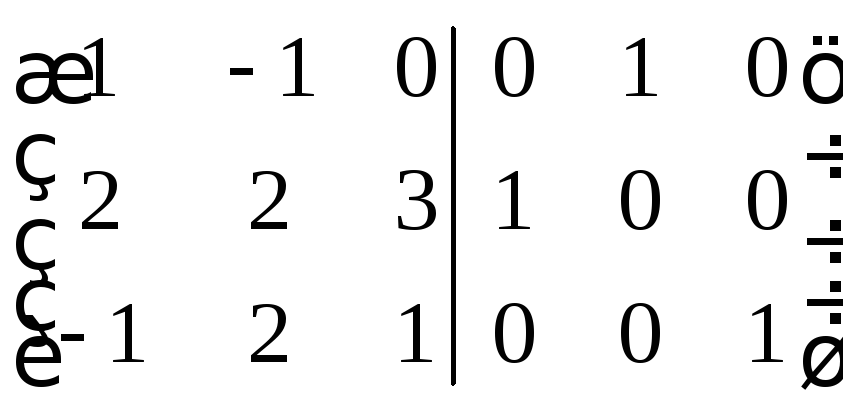
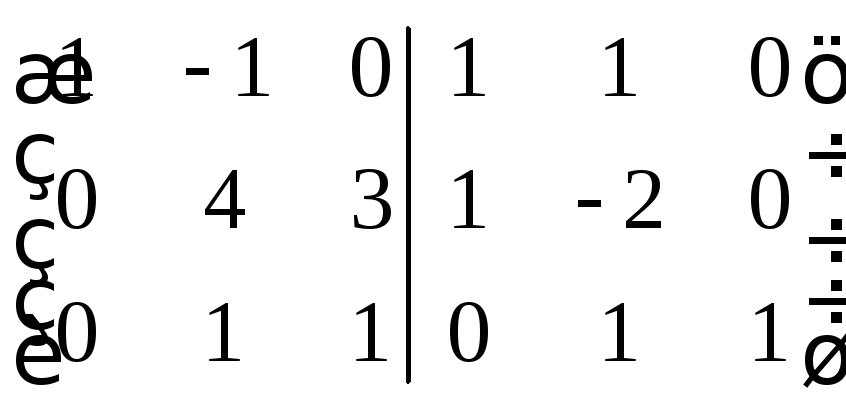
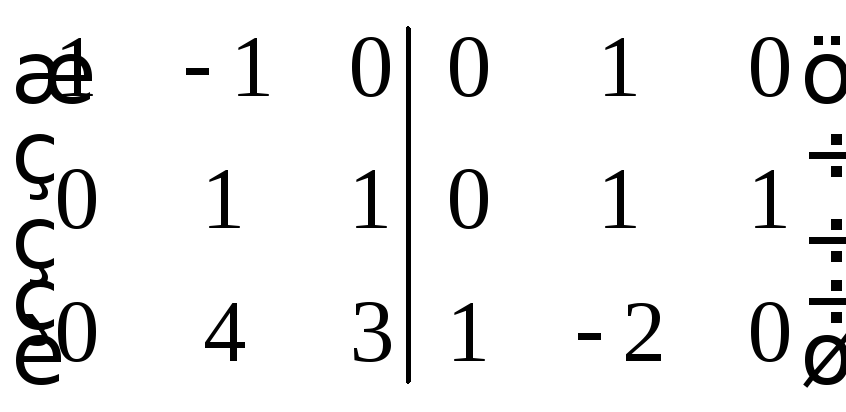
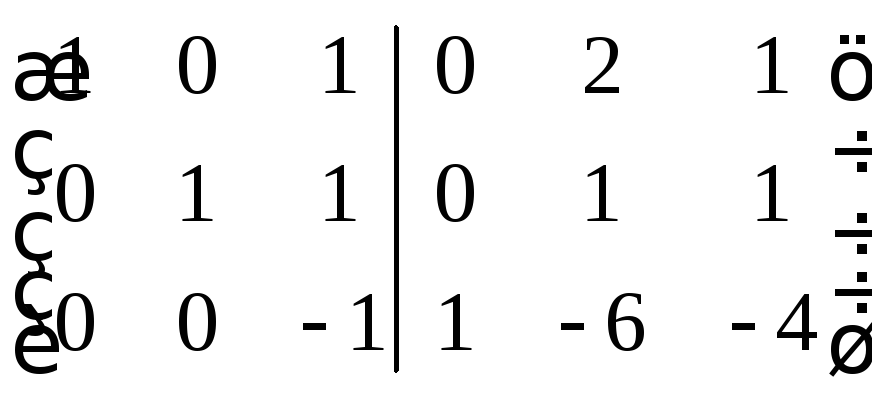
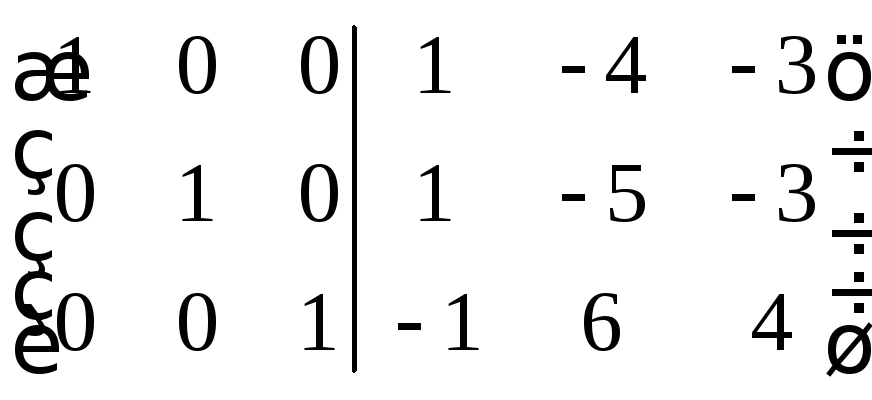Отже, .

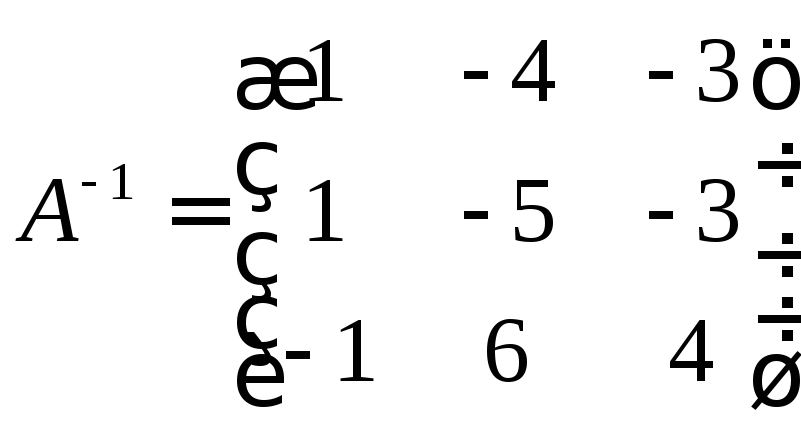Теорема 3.

Для не особливості матриці А завжди існує обернена і тільки одна.

► Нехай і- дві обернені матриці для А, тобто АВ = Е і А= Е. Помножимо другу рівність зліва на В, отримаємо ВА= ВЕ.

Оскільки ВА = Е, то маємо =В.◄