1

1. Множество – совокупность некоторых объектов. Примерами множеств являются множества чисел, множества точек прямой, множество линий и др. Каждое отдельное множество задается правилом или законом, позволяющим судить, принадлежит объект данному множеству или нет.

2. Подмножество - Множество A является подмножеством множества B, если любой элемент, принадлежащий A, также принадлежит B.

3. Универса́льное мно́жество — в математике множество, содержащее все объекты и все множества. Если универсальное множество существует, то оно единственно.

Универсальное множество обычно обозначается 

4. Существуют два основных способа задания множеств: перечисление и описание его элементов. Перечисление состоит в получении полного списка элементов множества, а описание заключается в задании такого свойства, которым элементы данного множества обладают, а все остальные нет.

5. Операции над множествами:

— объединение,  — пересечение,  — разность,  — симметрическая разность,

2

1. Множества чисел: Натуральные числа: N, Натуральные числа c включенным нулем: N0, Целые числа: Z, Целые положительные числа: Z+, Целые отрицательные числа: Z−, Рациональные числа: Q, Действительные числа: R, Комплексные числа: C

2. Действительное число - (вещественное число) , любое положительное, отрицательное число или нуль.

Модуль числа – это расстояние от начала отсчета до данного числа

Свойства модулей:

3. Числовые отрезки, интервалы, полуинтервалы и лучи называют числовыми промежутками.

4. Окрестность точки — множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней

3

1. Понятие функции- Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение перемен­ной у.

2. Основные способы задания функции: аналитический, табличный, графический, словесным описанием

3. Естественная область определения функции - множество тех значений ее аргумента, при которых формула имеет смысл.

4. Явной функцией от одной переменной называется функция вида: y = f(x), т.е. такая функция, которую можно явным образом выразить через зависящую переменную.

Неявной функцией от двух переменных называется функция вида F(x,y)=0, т.е. мы не можем выразить явным образом одну из переменных функции с помощью другой переменной, но мы знаем зависимость между этими переменными.

Параметрической функцией называется функция, у которой каждый аргумент зависит от некоторого параметра, либо от нескольких параметров. Общий вид параметрической функции от одного параметра с двумя аргументами:

5. График функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией: точка (x,y) располагается (или находится) на графике функции f тогда и только тогда, когда y=f(x).

4.

Основные элементы поведения функции:

1) Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

2) Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

3) Периодическость функции - Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5)  Ограниченная и неограниченная функции. - Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

5.

Основные элементарные функции (степенные)

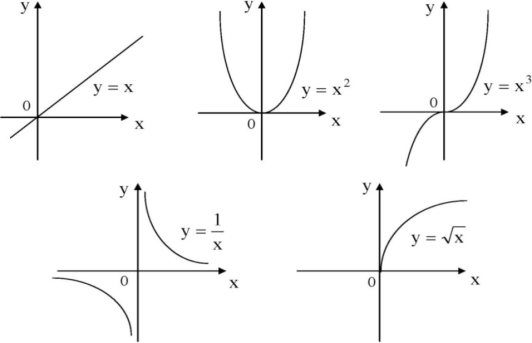
Степенная функция Свойства функции.1.  Если х = 0, то у = 0, т.е. график функции имеет с осями коорди­нат общую точку (0; 0) - начало координат.2.  Если х > 0, то у > 0, т.е. все точки графика функции, крoме на­чала координат, лежат над осью абсцисс.3.  Множеством значений функции  является промежуток [0;+∞).4. Функция  не является ни четной, ни нечетной.5. Функция  возрастающая в области определения.6.  Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует.

Степенная функция у=х² 1. D(x)=R – функция определена на все числовой оси; 2. E(y)=[0;∞) - функция принимает положительные значения на всей области определения; 3. При х=0 у=0 - функция проходит через начало координат O(0;0). 4. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞). 5. Функция является четной (симметрична относительно оси Оу).

Степенная функция y=x3 обладает следующими свойствами: 1. D(x)=(-∞;0)U(0;∞) для любого n; 2. E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число; 3. Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число. 4. Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число. 5. Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.

Степенная функция y=1/x обладает следующими свойствами: 1. D(x) ÎR, если n – нечетное число и D(x)=[0;∞), если n – четное число ; 2. E(y) Î (-∞;0)U(0;∞), если n – нечетное число; E(y)=[0;∞), если n – четное число; 3. Функция возрастает на всей области определения для любого числа n. 4. Функция проходит через начало координат в любом случае.

6.

Основные элементарные функции (тригонометрические)

Функция y = sin (х). 1. Область определения D(x) ÎR. 2. Область значений E(y) Î [ - 1; 1]. 3. Функция периодическая; основной период равен 2π. 4. Функция нечетная . 5. Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Î Z.

Функция y = cos(х). 1. Область определения D(x) ÎR. 2. Область значений E(y) Î [ - 1; 1]. 3. Функция периодическая с основным периодом 2π. 4. Функция четная. 5. Функция убывает на промежутках [2πn; π+ 2πn] и возрастает на промежутках [-π+ 2πn; 2πn], nπZ.

Функция y = tg х. 1. Область определения: D(x) Ï π/2 + πk, kÎZ. 2. Область значений E(y) Î (- ∞; + ∞) 3. π- основной период функции. 4. Функция нечетная. 5. Функция возрастает на промежутках ( -π/2 +πn;π/2 +πn).

Функция y = ctg х. 1. Область определения функции: D(x) Ï xπ/2 +πk, kÎZ. 2. Область значений функции E(y) Î (- ∞; + ∞). 3. Функция периодическая с основным периодом π. 4. Функция нечетная. 5. Функция у = ctg х убывает на промежутках (πn;π+πn).

7.

Основные элементарные функции (обратные тригонометрические)

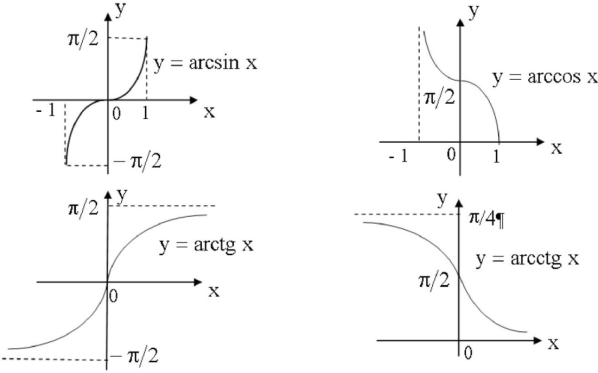
Функция y = arcsin ( x ): Свойства функции y = arcsin (x): 1. Область определения D(x)Î[−1;1] 2. Область значения E(y)Î [−π/2;π/2] 3. y=arcsin(x)- непрерывная строговозрастающая функция на D 5. График y = arcsin(x) симметричен графику y = sin(x) относительно линии y=x 6. y=arcsin(x) нечетная функция т.е. ∀x∈[−1;1] arcsin(−x)=−arcsin(х)

Функция y = arccos ( x ): Свойства функции y = arccos (x): 1. Область определения D(x)Î[−1;1] 2. Область значения E(y)Î [0;π] 3. y=arccos(x)- непрерывная строговозрастающая функция на D 5. График y = arccos(x) симметричен графику y = cos(x) относительно линии y=x 6. y=arccos(x) функция общего вида

Функция y = arccos ( x ): Свойства функции y = arccos (x): 1. Область определения D(x)Î[−1;1] 2. Область значения E(y)Î [0;π] 3. y=arccos(x)- непрерывная строговозрастающая функция на D 5. График y = arccos(x) симметричен графику y = cos(x) относительно линии y=x 6. y=arccos(x) функция общего вида

Функция y = arc с tg ( x ): Свойства функции y = arcсtg (x): 1. Область определения D(x)Î(- ∞;+∞) 2. Область значения E(y)Î [0 ; π] 3. y=arctg (x)- непрерывная строгоубывающая функция на D 4. График y = arcсtg(x) симметричен графику y = сtg(x) относительно линии y=x 5. y=arcctg(x) функция общего вида.

8.

Основные элементарные функции (показательная, логарифмическая)

Показательная

Основные свойства показательной функции : 1. Область определения — множество (R) всех действительных чисел. 2. Область значений — множество (R+) всех положительных действительных чисел. 3. При а > 1 функция возрастает на всей числовой прямой; при 0<а<1 функция убывает. 4. Является функцией общего вида.

Логарифмическая

Логарифмическая функция у = loga x обладает следующими свойствами : 1. Область определения D(x)Î (0; + ∞). 2. Область значений E(y) Î ( - ∞; + ∞) 3. Функция ни четная, ни нечетная (общего вида). 4. Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0 < а < 1.

9.

Простейшие элементарные функции

Прямая линия - график линейной функции y = ax + b. Функция монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)

Парабола - график функции квадратного трёхчлена у = ах2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0

Дробно-линейной функцией называется функция, заданная формулойгде . Область определения этой функции . 1. При возрастании положительных значений аргумента значения функции убывают и стремятся к нулю, но остаются положительными. 2. При возрастании положительных значений функции значения аргумента убывают и стремятся к нулю, но остаются положительными.

Функция y = |x|

Свойства функции 1.  Если х = 0, то у = 0, т.е. график пересекает оси координат в точке (0; 0) - начале координат.2.  Если х ≠ 0, то у > 0, т.е. все точки графика   функции  y = |x|,   кроме   начала координат, лежат над осью абсцисс.3.   Множеством значений функции y = |x|  является промежуток [0;+∞).4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. график функции симметричен относительно ординат (функция y = |x| - четная).5.  На промежутке [0;+∞) функция y = |x|  возрастает.6. На промежутке (-∞;0] функция y = |x|  убывает.7.  Наименьшее значение функция принимает в точке х, оно равно 0. Наибольшего значения не существует.

10.

Понятие обратной и сложной функции

Функция называется обратной, если для любых двух различных чисел и , принадлежащих , числа и также различны.

Пусть даны две функции:  и , тогда функция  называется сложной функцией. Это когда одна функция находится внутри другой функции, т.е. аргументом функции является другая функция.

Элементарные функции, их классификация.

Функции, которые могут быть получены из основных элементарных функций посредством арифметических действий и образования сложных функций, называются элементарными функциями.

Элементарные функции: Трансцендентные, Алгебраические (Иррациональные, Рациональные (Целые рациональные, Дробные рациональные))

11. Функцией y=f(x) называется отображение множества X на множество Y, причем каждому элементу ставится в соответствие единственный элемент.

Числовой последовательностью x₁,x₂,x₃…,x_n называется функция x_n=f(n), заданная на множестве N натуральных чисел. Обозначается 

Последовательность называетсяограниченной, если существует такое число M>0, что для любого выполняется неравенство.

Пример: геометрическая прогрессия с основанием (1;;;;;;)

Монотонная последовательность – последовательность ,, удовлетворяющая одному из условий:

1)Для любого n выполняется неравенство (возрастающая)

Пример: последовательность Фибоначчи (1;1;2;3;5;8;13)

2)Для любого n выполняется неравенство (убывающая)

Пример: геометрическая прогрессия с основанием (1;;;;;;).

12. В дальнейшем курсе математики понятие предела будет играть фундаментальную роль, так как с ним непосредственно связаны основные понятия математического анализа – производная, интеграл и др.Начнем с понятия предела числовой последовательности.Число a называется пределом последовательности x = {x_n}, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |x_n - a| < ε.Если число a есть предел последовательности x = {x_n}, то говорят, что x_n стремится к a, и пишут .Чтобы сформулировать это определение в геометрических терминах введем следующее понятие.Окрестностью точки x₀ называется произвольный интервал (a, b), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x₀, для которой x₀ является серединой, тогда x₀ называется центром окрестности, а величина (b–a)/2 – радиусом окрестности.Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в видеЭто неравенство означает, что все элементы последовательности с номерамиn>N должны лежать в интервале (a – ε; a + ε).Следовательно, постоянное число a есть предел числовой последовательности {x_n}, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности точки a) найдется такой элемент последовательности с номером N, что все последующие элементыс номерами n>N будут находиться внутри этой окрестности. Сходящаяся последовательность — это последовательность элементов множества X, имеющая предел в этом множестве. Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.

13Определение. Ряды, все члены которых имеют одинаковые знаки, называются знакопостоянными. Для определенности, если это не будет оговорено особо, мы будем рассматривать ряды с положительными членами или знакоположительные ряды: P, Q, …: pn>0, qn>0 ,  Очевидно, что последовательность частичных сумм знакоположительных рядов монотонно возрастает: P1<P2< … <Pn<Pn+1< … . Следовательно, верна  Теорема. Для сходимости знакоположительного ряда необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

14Последовательность называется бесконечно малой последовательностью (б.м.п.),если для любого существует номер такой, что для любого выполняется неравенство:Последовательность называется бесконечно большой (б.б.п.), если для любого существует номер такой, что для любого выполняется неравенство: Основные свойства б.м. и б.б. последовательностей 1°   Сумма б.м. последовательностей есть б.м.п. 2.Произведение ограниченной последовательности и б.м. есть б.м.п. 3°   Если - б.м.п., то - ограниченная последовательность.4°   Произведение б.м.п. есть последовательность б.м.5°   Если - б.м.п. и , то , т.е. 6°   Если - б.м.п. и , то последовательность - б.б.п.7°   Если - б.б.п., то и последовательность - б.м.п.

15-------

16Функция называетсябесконечно малой при , если.Функцияназываетсябесконечно большой при , если для любого положительного числасуществует такое число, что для всех, удовлетворяющих неравенству, выполняется неравенство. Записывается: .Свойства бесконечно малых функций:1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2)Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.

3)Произведение двух бесконечно малых функций есть функция бесконечно малая.

4)Произведение бесконечно малой функции на число есть функция бесконечно малая.

5)Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.

Теорема о связи между бесконечно большой и бесконечно малой функциями:Если функция - функция бесконечно малая (), то функцияесть бесконечно большая функция и наоборот.Доказательство:Пусть - бесконечно малая функция при, т.е.. Тогда для любого числасуществует такое число, что для всех, удовлетворяющих неравенству, выполняется неравенство, т.е., т.е., где. А из этого следует, что функция- бесконечно большая.

17До сих пор мы рассматривали свойства интегралов, выражаемые равенствами; перейдем теперь к таким, которые выражаются неравенствами.

5°. Если функция интегрируемая в промежуткенеотрицательна ито

Доказательство очевидно.Труднее доказать более точный результат:Если функция интегрируемая в промежуткеположительна и, то

18 Первый замечательный предел имеет вид: На практике чаще встречаютсямодификации первого замечательного предела в виде где,k – коэффициент.Пояснение: Следствия первого замечательного предела:

1. 2

19Второй замечательный предел имеет вид:или в другой записи

В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность .Разберем несколькопримеров нахождения предела по второму замечательному пределу сподробным оприсанием решения.

20. Исследование функции на непрерывность связано с нахождением односторонних пределов функции. Так что рекомендуем ознакомится с разделом Предел функции, основные определения и понятия, прежде чем двигаться дальше.Определение непрерывности функции в точке.Функция f(x) называется непрерывной в точке , если предел слева равен пределу справа и совпадает со значением функции в точке , то есть .

Следствие.ЗНАЧЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ НЕПРЕРЫВНОСТИ СОВПАДАЕТ СО ЗНАЧЕНИЕМ ФУНКЦИИ В ЭТИХ ТОЧКАХ.

21. Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке

Определение 4. Функция называется непрерывной на отрезке , если она непрерывна в каждой точке этого отрезка (в точке a непрерывна справа, т.е. , а в точке b непрерывна слева, т. е. ).

Все основные элементарные функции непрерывны в области их определения.

Свойства функций, непрерывных на отрезке:

1) Если функция непрерывна на отрезке , то она ограничена на этом отрезке (первая теорема Вейерштрасса).

2) Если функция непрерывна на отрезке , то на этом отрезке она достигает своего наименьшего значения и наибольшего значения (вторая теорема Вейерштрасса) (см. рис. 2).

3) Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то внутри отрезка существует хотя бы одна точка такая, что (теорема Больцано-Коши).

22.Комплексным числомназывается выражение вида a + ib, где a и b – любые действительные числа, i – некоторый символ, который называетсямнимой единицей. Часто используют символическую запись.

Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z.

Сопряженным (или комплексно сопряженным) числом к комплепрксному числу называется число .

Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + b·i обозначается |a + b·i|, а также буквой r. Из чертежа видно, что:

r₌ | a₊b·i |₌

a2+b2

Модуль действительного числа, совпадает с его абсолютным значением. Сопряженные комплексные числа a + b·i и a - b·i имеют один и тотже модуль.

Алгебраическая форма комплексного числа

Запись комплексного числа в виде, гдеи- действительные числа, называетсяалгебраической формойкомплексного числа.