Министерство образования Республики Беларусь

Учреждение образования

«Минский государственный высший

радиотехнический колледж»

Реферат

на тему: «Метод Монте-Карло. Алгоритм Гомори.

Задача Коммивояжера»

Выполнила	/Гилевская И. С./
Проверил	/Батура А. В./

2013

Метод Монте-Карло

Ме́тод Мо́нте-Ка́рло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии, математики, экономики, оптимизации, теории управления и др.

Интегрирование методом Монте-Карло

Предположим, необходимо взять интеграл от некоторой функции. Воспользуемся неформальным геометрическим описанием интеграла и будем понимать его как площадь под графиком этой функции.

Для определения этой площади можно воспользоваться одним из обычных численных методов интегрирования: разбить отрезок на подотрезки, подсчитать площадь под графиком функции на каждом из них и сложить. Предположим, что для функции, представленной на рисунке 2, достаточно разбиения на 25 отрезков и, следовательно, вычисления 25 значений функции. Представим теперь, мы имеем дело с n -мерной функцией. Тогда нам необходимо 25ⁿ отрезков и столько же вычислений значения функции. При размерности функции больше 10 задача становится огромной. Поскольку пространства большой размерности встречаются, в частности, в задачах теории струн, а также многих других физических задачах, где имеются системы со многими степенями свободы, необходимо иметь метод решения, вычислительная сложность которого бы не столь сильно зависела от размерности. Именно таким свойством обладает метод Монте-Карло.

Геометрический алгоритм Монте-Карло интегрирования

Для определения площади под графиком функции можно использовать следующий стохастический алгоритм:

- ограничим функцию прямоугольником (n-мерным параллелепипедом в случае многих измерений), площадь которого S_par можно легко вычислить;

- «набросаем» в этот прямоугольник (параллелепипед) некоторое количество точек (N штук), координаты которых будем выбирать случайным образом;

- определим число точек (K штук), которые попадут под график функции;

- площадь области, ограниченной функцией и осями координат, S даётся выражением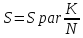

Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее, в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным.

Квантовый метод Монте-Карло

Квантовый метод Монте-Карло широко применяется для исследования сложных молекул и твёрдых тел. Это название объединяет несколько разных методов. Первый из них это вариационный метод Монте-Карло, который, по сути, является численным интегрированием многомерных интегралов, возникающих при решении уравнения Шрёдингера. Для решения задачи, в которой участвует 1000 электронов, необходимо взятие 3000-мерных интегралов, и при решении таких задач метод Монте-Карло имеет огромное преимущество в производительности по сравнению с другими численными методами интегрирования. Другая разновидность метода Монте-Карло — это диффузионный метод Монте-Карло.

Алгоритм Гомори

Алгори́тм Го́мори — алгоритм, который используется для решения полностью целочисленных задач линейного программирования. Алгоритм включает в себя:

1) Решение задачи одним из методов группы симплекс-методов или группы методов внутренней точки без учёта требования целочисленности. Если полученное оптимальное решение целочисленно, то задача решена.

2) Составляется дополнительное ограничение для переменной , которая в оптимальном плане имеет максимальное дробное значение, хотя должна быть целой. Тогда величины коэффициентов элементов , вычисляются так:

где — целая часть числа . Тогда дополнительное ограничение формируется следующим образом:

Оно будет целым неотрицательным при целых неотрицательных и . После составления ограничения оно вводится в систему линейных ограничений и задача решается заново при исходных ограничениях и дополнительном ограничении. Если получено целочисленное решение, задача решена. В противном случае необходимо повторить второй этап.

Задача коммивояжера

Коммивояжеру требуется посетить каждый город в пределах конкретной зоны обслуживания и возвратиться домой. Не приходится и говорить, что коммивояжеру хотелось бы выбрать такой порядок обхода клиентов, при котором его путь был возможно короче. Таким образом, коммивояжер сталкивается с задачей поиска маршрута минимальной протяженности, длительности или стоимости.

Задача коммивояжера может быть сформулирована как задача на графе в следующей постановке: построить граф G(Х, А), вершины которого соответствуют городам в зоне коммивояжера, а дуги отображают коммуникации, соединяющие пары городов. Пусть длина а(х, у)≥0 каждой дуги (х, у) ε А равна расстоянию, стоимости или времени. Контур, включающий каждую вершину графа G хотя бы один раз, называется маршрутом коммивояжера. Контур, включающий каждую вершину графа G ровно один раз, называется гамильтоновым контуром (по имени ирландского математика Вильяма Роуана Гамильтона, который в 1859 г. первым начал изучение этих задач).

Общей задачей коммивояжера называется задача поиска маршрута наименьшей общей длины.

Задачей коммивояжера называется задача поиска гамильтонова контура наименьшей общей длины. Контур коммивояжера, имеющий наименьшую длину, называется оптимальным маршрутом коммивояжера и является оптимальным решением общей задачи коммивояжера. Гамильтонов контур наименьшей длины называется оптимальным гамильтоновым контуром и является оптимальным решением задачи коммивояжера.

Оптимальный маршрут коммивояжера не обязательно является гамильтоновым контуром.

ТЕОРЕМА. Если для каждой пары вершин (х, у) графа G выполняется условие а (х, у) ≤а (х, z) + а (z, у) для всех z ≠ х, z ≠ у, то гамильтонов контур является решением общей задачи коимивояжера на графе G (если решение вообще существует).

Условие говорит только о том, что расстояние непосредственно от х до у никогда не превышает расстояния от х до у через любую другую вершину z. Условие называется неравенством треугольника.

ДОКАЗАТЕЛЬСТВО. Предположим, что не существует оптимального решения общей задачи коммивояжера, представляющего собой гамильтонов контур. Пусть С — любой оптимальный маршрут коммивояжера. Так как С не является гамильтоновым контуром, то некоторая вершина, скажем вершина z, повторяется в маршруте С по крайней мере дважды. Предположим, что первый раз коммивояжер в вершину z пришел из вершины х и вышел из нее в направлении вершины у. Изменим маршрут С таким образом, чтобы коммивояжер из вершины х, минуя z, направился прямо к вершине у. Полученный в результате маршрут С' также является маршрутом коммивояжера, поскольку в нем каждая вершина посещается по крайней мере один раз. Кроме того, в соответствии с условием, общая длина С' не превышает длины С. Заменяя С на С' и повторяя эту процедуру, мы получим другой маршрут C'' и т. д. В конце концов этот процесс приведет нас к оптимальному маршруту, являющемуся гамильтоновым контуром, так как каждый последующий маршрут имеет число дуг на единицу меньшее, чем его предшественник. Теорема доказана.

Из теоремы следует, что если граф G удовлетворяет неравенству треугольника, то оптимальное решение задачи коммивояжера на графе G является оптимальным решением для общей задачи коммивояжера на этом графе.

Есть простой способ избежать разработки двух разных методов решения для задачи коммивояжера и общей задачи коммивояжера. Если граф G не удовлетворяет неравенству треугольника, то следует заменить длину а(х, у) каждой дуги (х, у), не удовлетворяющей этому неравенству, длиной кратчайшего пути от вершины х к вершине у.

Заметьте, что длина дуги от х к у отображает теперь передвижение коммивояжера от вершины х к вершине у вдоль кратчайшего пути, соединяющего эти вершины, а не напрямую из х в у, и длина удовлетворяет неравенству треугольника. Если оптимальное решение задачи коммивояжера на графе G включает некоторую дугу (х, у), длина которой уменьшена описанным выше способом, то в оптимальном решении эту дугу следует заменять дугами, входящими в кратчайший путь между вершинами х и у.

Предположим, что мы желаем вместо гамильтонова контура наименьшей длины найти гамильтонов контур, имеющий максимальную длину. Пусть тперь через М обозначена наибольшая длина дуги в графе G. Пусть далее

а' (х, y)= М- а (х, у)≥0 для всех дуг (х, у) (1)

Каждый гамильтонов контур на графе G = (Х, А) содержит ровно |Х| дуг. Оптимальный (в смысле наименьшей длины) гамильтонов контур С включает дуги, преобразованные в соответствии с соотношением (1), и его общая длина равна

Таким образом, гамильтонов контур минимальной длины, состоящий из преобразованных дуг, эквивалентен гамильтонову контуру максимальной длины, составленному из тех же дуг с исходной (не преобразованной) длиной.

Следовательно, для нахождения гамильтонова контура максимальной длины достаточно решить задачу коммивояжера, предварительно преобразовав длины дуг графа в соответствии с (1). Однако не все графы имеют гамильтонов контур. Например, граф, состоящий только из двух вершин х и у и одной дуги (х, у), такого контура не имеет.