
- •РАБОЧАЯ ПРОГРАММА
- •СОДЕРЖАНИЕ
- •Тема 1. ОБЩИЕ СВЕДЕНИЯ О МЕТОДАХ ОПТИМИЗАЦИИ
- •1.1. Основные понятия и определения. Постановка задачи
- •Тема 2. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- •2.2. Определение выпуклости функций
- •2.3. Типы задач математического программирования
- •2.4. Связь между задачей математического программирования
- •Тема 3. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- •3.3. Симплекс-метод решения задач ЛП
- •3.4. Симплекс-таблицы
- •3.5. Метод искусственного базиса
- •3.6. Информационные технологии линейного программирования
- •3.7. Двойственная задача линейного программирования
- •3.8. Двойственный симплекс-метод
- •3.9. Целочисленное линейное программирование
- •3.9.1. Алгоритм Гомори для полностью целочисленной задачи ЛП.
- •3.9.2. Алгоритм Гомори для частично целочисленной задачи.
- •3.9.3. Метод ветвей и границ решения целочисленных задач ЛП.
- •Тема 4. ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ БЕЗ ОГРАНИЧЕНИЙ
- •4.1. Одномерная минимизация унимодальных функций
- •4.1.1. Метод Фибоначчи.
- •4.1.2 Метод золотого сечения.
- •4.1.3. Методы с использованием производных.
- •4.1.4. Методы полиномиальной аппроксимации.
- •4.2.2. Градиентные методы. Метод наискорейшего спуска.
- •4.2.4. Метод Дэвидона-Флетчера-Пауэла (ДФП) (метод переменной мет-
- •4.2.6. Обобщенный градиентный алгоритм.
- •4.2.7. Метод Ньютона.
- •4.2.9. Установка метода оптимизации в пакете MATLAB.
- •Тема 5. ЭКСТРЕМАЛЬНЫЕ НЕЛИНЕЙНЫЕ ЗАДАЧИ
- •5.1. Метод неопределенных множителей Лагранжа
- •5.2. Теорема Куна-Таккера
- •5.3. Квадратичное программирование
- •5.4. Метод допустимых направлений Зойтендейка
- •6.1. Метод линейных комбинаций
- •6.2. Метод отсекающих плоскостей Кэлли
- •6.3. Сепарабельное программирование
- •ТЕМА 7. МЕТОДЫ ОПТИМИЗАЦИИ УПРАВЛЕНИЯ
- •7.1. Дискретное динамическое программирование
- •7.3. Принцип максимума Понтрягина
- •7.3.1. Постановка задачи. Формулировка принципа максимума.
- •7.3.3. Принцип максимума в задачах о максимальном быстродействии.
- •7.4.1. Определение моментов переключения.
- •ЛИТЕРАТУРА
- •Содержание
- •Лабораторная работа № 1
- •Лабораторная работа № 2
- •Лабораторная работа № 3
- •Лабораторная работа № 4
- •ЗАДАНИЯ ПО КУРСОВОЙ РАБОТЕ
- •Задание 1. Линейное программирование
- •Задание 2. Нелинейное программирование
- •Задание 3. Математическое описание линейных систем
|
|
|
|
F(x3 ) < F(x3 ) , поэтому x* [8,10] и подинтервал [8,10] исключается. |
|||||||||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4-й шаг. Остается интервал [5,8] . Точка x3 сохраняется внутри оставшегося |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
интервала, |
поэтому x4 |
= x3 = 7 . На первом шаге выполнено 2 |
эксперимента, на |
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
втором и на третьем – по одному, поэтому осталось провести последний пятый |
|||||||||||||||
эксперимент. |
|
|
|
|
|
x4 |
= x4 − ε. Сравнивая значе- |
||||||||
|
|
|
5-й шаг. Выполним 5-й эксперимент в точке |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
ния функции F(x4 ) |
и |
F(x4 ) , сокращаем подинтервал [7,8]. Окончательно получа- |
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
ем, что оптимальное решение x* локализировано в апостериорном интервале [5,7]. |
|||||||||||||||
|
|
|
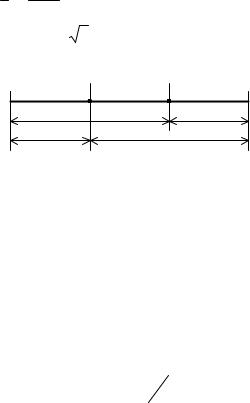
4.1.2 Метод золотого сечения. Золотым сечением отрезка называется деле- |
||||||||||||
ние его на две неравные части так, что отношение длины всего отрезка к длине |
|||||||||||||||
большей части равно отношению длины большей части к длине меньшей части |
|||||||||||||||
отрезка. Рассмотрим отрезок единичной длины (рис. 4.3) и две точки x1 и x2 на |
|||||||||||||||
нем, каждая из которых делит отрезок в отношении золотого сечения. Тогда |
|||||||||||||||
1 |
= |
1 |
τ , |
|
откуда |
|
τ2 + τ −1 = 0 |
и |
положительное |
значение |
|||||
τ |
|
|
− τ |
5) / 2 = 0,61803... ≈ 0,62 . Величина 1 − τ = τ2 |
|
|
|
||||||||
τ = (−1 + |
≈ 0,38 . |
|
|
||||||||||||
0 |
|
|
|
|
x1 |
x2 |
|
1 |
Таким образом, в методе золотого |
||||||
|
|
|
|
|
сечения координаты точек |
экстремума |
|||||||||
|
|
|
|
|
|
τ |
|
|
|
1 − τ |
на единичном интервале определяются |
||||
|
|
|
1 − τ |
|
|
|
|
τ |
|
следующим |
образом: |
x1 ≈ 0,38; |
|||
|
Рис. 4.3. Золотое сечение отрезка |
x2 ≈ 0,62 . Если F(x) задается на апри- |
|||||||||||||
|
орном интервале [a, b] , то точки экспе- |
||||||||||||||
|
|
= a + τ2 |
|
|
|
|
|
римента |
вычисляются |
по |
формулам |
||||
x |
|
(b − a) ; |
x |
2 |
= a + τ(b − a) и равно отстоят от концов отрезка. В точках |
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
эксперимента вычисляется значение функции F(x) . |
|
|
|
||||||||||||
|
|
|
Сокращение интервала неопределенности осуществляется по тому же прин- |
||||||||||||
ципу, который изложен в предыдущем разделе при рассмотрении метода Фибо- |
|||||||||||||||
наччи. Точки эксперимента на любой итерации равноудалены от границ интерва- |
|||||||||||||||
ла, и на каждом следующем шаге процедуры поиска должно вычисляться только |
|||||||||||||||
одно значение функции в получаемой точке. После каждого шага текущий интер- |
|||||||||||||||
вал сокращается в |
1 |
τ |
раз. После проведения N испытаний апостериорный интер- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вал неопределенности определяется выражением |
LN |
= (b − a) τN −1 . Поиск за- |
|||||||||||||
канчивается, когда длина интервала неопределенности становится соизмеримой с |
|||||||||||||||
точностью решения задачи. |
|
|
|
|
|
||||||||||
55

Анализ метода Фибоначчи и метода золотого сечения показывает, что, начи-
ная с некоторого числа значения экспериментов N, FN −1 ≈ τ2 , следовательно, точ-
FN +1
ки испытаний на первом шаге практически одинаковы в обоих методах. Так, при
N = 5 отношение |
F4 |
= |
|
5 |
|
≈ 0,384 , а τ2 = 0,382 . Этот факт позволяет реализовы- |
F |
13 |
|||||
6 |
|
|
|
|
|
|
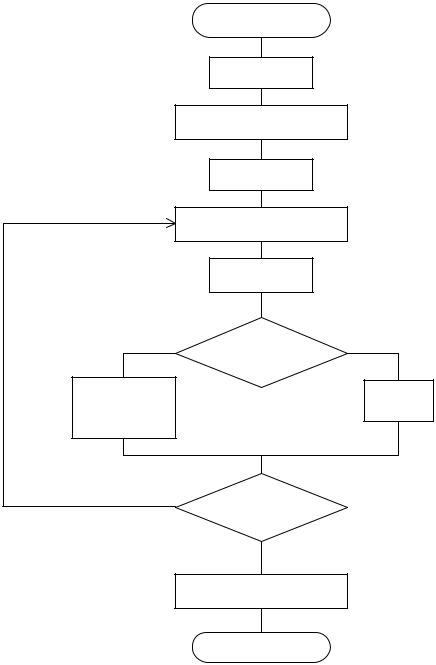
вать оба метода в виде единой процедуры поиска минимума унимодальной функции F(x) , определенной на интервале [ 0 ,1] (рис. 4. 4).
4.1.3. Методы с использованием производных. Эффективность процедуры поиска экстремума можно повысить, если ввести требование дифференцируемо-
сти функции. Необходимым условием существования минимума в точке x* является равенство нулю первой производной функции в этой точке, т.е.
F ' ( x* ) = dF |
|
x = x |
* = 0 . |
|
|||
dx |
|
|
|
|
|
Если функция F(x) содержит члены, включающие x в третьей и более высоких степенях, то получение аналитического решения уравнения F ' (x) = 0 может
оказаться затруднительным. В таких случаях используются приближенные методы последовательного поиска точки экстремума.
Метод Ньютона-Рафсона. Будем полагать, что функция F(x) дважды дифференцируема. Пусть точка xk является текущим приближением к точке экстре-
мума на k-ом шаге. Осуществим линеаризацию функции F ' (x) в точке xk . В ре- |
||
~' |
' |
(x) : |
зультате получим линейное приближение F |
функции F |
|
|
|
~ |
+ F '' (xk )(x |
− xk ) , |
(4.7) |
|
|
|
F ' (x, xk ) = F ' (xk ) |
||||
′′ |
k |
) – значение второй производной функции F(x) в точке xk . |
|
|||
где F (x |
|
|
||||
Приравняв правую часть уравнения (4.7) к нулю, получим следующее выра- |
||||||
жение для очередной точки xk +1 : |
|
|
|
|
||
|
|
xk +1 = xk |
− |
F ' ( xk ) |
. |
(4.8) |
|
|
F '' ( xk ) |
||||
|
|
|
|
|
|
|
56
x1 = 0, x2 =1 γ = τ2
x |
3 |
= x +γ (x |
2 |
− x ) |
γ = |
FN −1 |
|
||||||
|
1 |
1 |
|
FN +1 |
||
|
|
|
|
|
|
F1 = F(x3 )
x4 = x1 + (x2 − x3 )
F2 = F(x4 )
|
F2 > F1 |
x1 = x3, x3 = x4 |
x2 = x4 |
F1 = F2 |
|
x* = x3, Fmin = F1
Рис. 4.4. Алгоритм поиска минимума унимодальной функции методом Фибоначчи и методом золотого сечения
Графическая интерпретация процедуры поиска методом Ньютона-Рафсона приведена на рис. 4.5, а. Точка x0 является начальной оценкой корня уравнения
F ' (x) = 0 (или начальной оценкой координаты точки экстремума). Касательная к
57
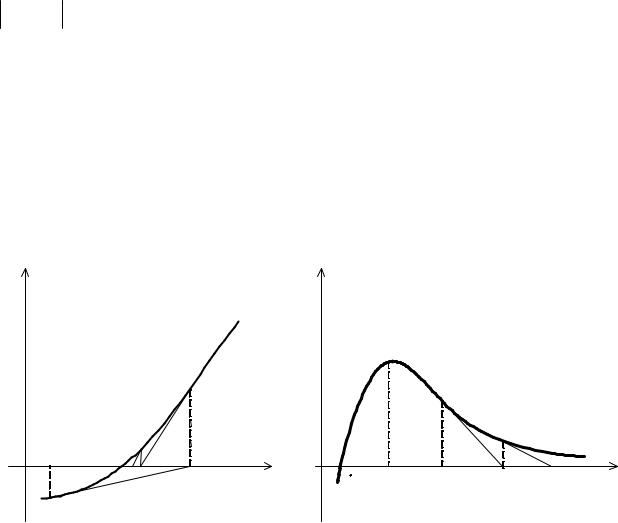
функции F ' (x) в точке x0 является линейной аппроксимацией функции F(x) в точке x0 . Точку пересечения этой касательной с осью абсцисс принимают за новую точку x1, в которой проводят следующую касательную к функции и т.д. Итерации продолжаются до тех пор, пока не будет выполняться неравенство F ' ( xk ) ≤ ε , где ε – заранее заданная точность решения задачи.
В зависимости от выбора начальной точки x0 и вида функции F ' (x) алгоритм
может расходиться (рис. 4.5, б). Если x0 расположена правее точки z, то получаемые в результате последовательных приближений точки удаляются от x*. Для улучшения сходимости используют модифицированный метод, в котором вводится шаг αk [0,1] . При этом процесс отыскания нуля производной задается форму-
лой:
|
|
F ' (xk ) |
. |
(4.9) |
|
xk +1 = xk − αk F '' (xk ) |
|
||
′ |
′ |
|
||
F (x) |
F (x) |
|
||
x |
0 |
x* |
x |
2 |
x |
1 |
x |
x* |
|
|
x |
|
|
x3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Z |
x0 |
x1 |
x2 |
|
|
|
|
|
|
а |
|
|
|
|
б |
|
Рис. 4.5. Графическая интерпретация метода Ньютона-Рафсона: а – сходимость метода; б – отсутствие сходимости
Метод хорд, или метод «секущих» является комбинацией метода Ньютона-Рафсона и общей схемы исключения интервалов и заключается в нахо-
ждении корня уравнения F ' (x) = 0 в интервале [a, b] , если такой корень
существует.
Для решения задачи в интервале [a, b] выбираются две точки M и N, в которых знаки производных различаются. Функция F ' (x) аппроксимируется «секу-
58
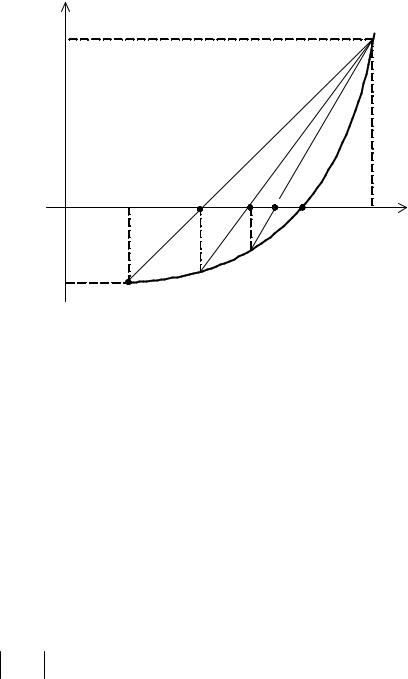
щей» прямой, соединяющей F ' (M ) и F ' (N ) и находится точка z , в которой прямая линия пересекает ось абсцисс (рис. 4.6).
F ′(x)
F ′(N )
M |
Z Z1 Z2 |
N x |
x*
F′(M )
Рис. 4.6. Графическая интерпретация метода хорд
Уравнение прямой, проходящей через две точки с координатами (x1, y1) и (x2 , y2 ) , имеет вид
|
|
|
|
|
y − y1 |
|
= |
x − x1 |
. |
|
|
||||
|
|
|
|
|
y |
2 |
− y |
|
|
x |
2 |
− x |
|
||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|||
Заменим текущие координаты x и y координатами точки пересечения оси х, |
|||||||||||||||
тогда 0 − F ' (M ) |
= |
z − M и координата z вычисляется по формуле |
|
||||||||||||
|
F ' (N ) − F ' (M ) |
N − M |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
z = M − |
F ' (M )(N − M ) |
. |
(4.10) |
||||||||
|
|
|
|
F ' (N ) − F ' (M ) |
|
|
|||||||||
Если F ' (z) ≤ ε, поиск следует прекратить. В противном случае необходимо
выбрать одну из точек M или N таким образом, чтобы знаки производной в этой точке и точке z были различными, и снова повторить основной шаг алгоритма.
59
