
конспект инжинерная графика
.pdf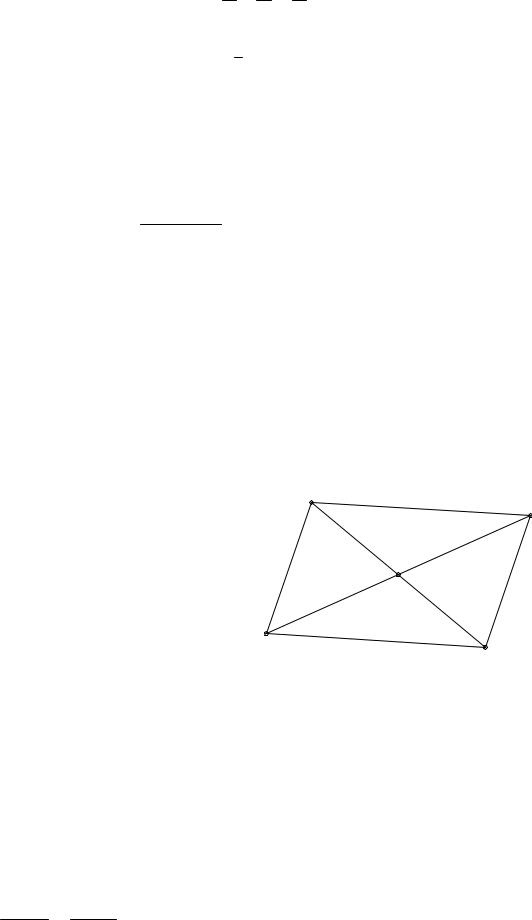
71
T1 +T2 +T3 = aa1 + aa2 + aa3 =1.
З урахуванням умови (1) одержимо:
3T3 =1 =>T3 = 13
А. Мьобіус одержав основне рівняння точкового числення у виді:
T = T1 A +T2 B +T3C ,
де T1,T2,T3 – нормовані барицентричні координати, що задовольняють визначеній умові.
Це рівняння в інтерпретації геометричного застосування поняття центра ваги трикутника може бути представлене у виді:
T = A + B + C
3
Далі, факт представлення однієї точки як лінійної комбінації декількох інших Мьобіус поклав в основу класифікації лінійних перетворень, виділивши відповідно до групи перетворень евклідову, афінну, проективну та конформну геометрії.
Довгий час точкове числення знаходило застосування у механіці для знаходження точки додатка (центроїди) і величини рівнодіючої системи рівнобіжних сил. У математичному і комп'ютерному моделюванні воно стало застосовуватися зовсім недавно, головним чином у докторській дисертації І.Г. Балюби.
Для інтерпретації обчислювальної геометрії на площині та у просторі використовується не тільки точкове, але й інше пряме числення – векторне. З використанням останнього І.Г. Балюбою була введена метрика, що забезпечила відтворення геометричної
форми обчислювальними формами. |
A |
L |
|
||
|
|
N
B
Рис. 4.14 C
Питання точкового завдання кривих і поверхонь, визначених параметрично вирішуються таким чином, що завдання плоских геометричних образів розглядаються в симплексі точок A, B, C і D.
Наприклад, розглянемо задачу: Задані точки паралелограма A, B, C (рис. 4.14). Необхідно добудувати відсутню вершину L.
Розв’язання. Діагоналі паралелограма поділяються навпіл. Таким чином, точка перетину діагоналей є середнє арифметичним від протилежних вершин:
N = A +2 C = B +2 L => L = A +C − B
72
4.8.3. ВЕКТОРНИЙ ДОБУТОК ВЕКТОРІВ ТА ЇХ ІНТЕРПРЕТАЦІЯ В ТОЧКОВОМУ ЧИСЛЕННІ.
Поставлено задачу застосування точки виходу з площини та метричного оператора. Нехай ABC довільно розташований у просторі. Приймаємо координатні площини за
площини проекцій: |
|
|
|
|
|
Z |
|
||
OE1E3≡П2; OE1E2≡П1; OE2E3≡П3, |
|
|
|
|
|||||
де OE1, OE2, OE3 – одиничні взаємо- |
|
|
|
|
|||||
перпендикулярні вектори, що позначимо |
|
|
|
|
|||||
як OE1=i; OE2=j, OE3=k, що задають |
|
|
|
|
|||||
прямокутну |
декартову |
систему |
|
|
E3 |
П3 |
|||
координат O, i, j, k. |
|
|
П2 |
|
|
k |
|||
Розглянемо |
трикутник |
ABC |
у |
E1 |
i |
|
|||
проекціях |
відповідно на площинах |
П1, X |
O |
|
|||||
П2, П3 за законами нарисної геометрії, де |
|
|
j |
||||||
|
|
|
|||||||
введемо позначення: |
|
П1 |
|
|
|
E2 |
|||
Sxy |
– |
|
подвійна |
площа |
|
|
|
||
горизонтальної проекції ABC; |
|
|
|
Рис. 4.15 |
|
|
|||
Syz – подвійна площа профільної |
|
|
|
Y |
|||||
|
|
|
|||||||
проекції |
ABC; |
|
|
|
|
|
|
|
|
Szx – подвійна площа фронтальної проекції |
ABC. |
|
|
|
|||||
Твердження. Для будь-якого трикутника ABC точка S, що має координатами орієнтовані подвійні площі проекцій цього P
трикутника на координатні площини, утворить
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
||
вектор |
|
OS , |
перпендикулярний |
цьому |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
трикутникові. Довжина вектора |
|
OS |
|
дорівнює |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
подвійній площі трикутника ABC, тобто S ABC. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Координати точки виходу (рис. 4.16) із |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
площини ABC визначаються з визначника: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
i |
|
|
j |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
X BA |
YBA |
ZBA |
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|||||||
|
|
|
|
|
X CA |
YCA |
ZCA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.16 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
Відзначимо, що приведена формула виражає точку S, а не точку P. |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
YBA |
ZBA |
|
|
|
YA |
Z A |
1 |
|
|
|
|
X BA |
ZBA |
|
|
|
X A |
Z A |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
X |
S |
= |
|
|
= |
Y Z |
B |
1 |
|
|
Y = |
|
= |
|
X |
B |
Z |
B |
1 |
; |
|
|||||||||||
|
|
YCA |
ZCA |
|
|
|
B |
|
|
|
|
|
|
; |
S |
|
X CA |
ZCA |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
YC |
ZC |
1 |
|
|
|
|
|
|
|
|
X C |
ZC |
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||

|
|
|
|
X BA |
YBA |
|
|
X A |
YA |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
ZS |
= |
= |
X B |
YB 1 |
; |
S(S yz ;S xz ;S xy ) . |
|
|
||||||
|
|
|
|
X CA |
YCA |
|
|
X C |
YC |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Твердження. Координати точки P, що визначає |
|
|
|||||||||||||
перпендикуляр AP до площини |
ABC, довжиною рівній OS, |
d |
S |
|||||||||||||
визначаються за формулами: |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
XP=XA+XS; YP=YA+YS; ZP=ZA+ZS. |
|
|
SABC |
||||||||
|
Визначення точки, розташованої на відстані d від |
|
||||||||||||||
|
|
|
||||||||||||||
площини |
ABC |
відноситься |
до |
задачі |
обчислювального |
|
|
|||||||||
інструментарію. |
|
|
|
|
|
|
|
|
|
|
O |
|||||
|
Нехай D – |
точка |
виходу з |
площини на відстань |
d |
|
||||||||||
|
|
Рис. 4.17 |
||||||||||||||
(рис. 4.17). Тоді завдання точки D, може бути здійснене за |
|
|||||||||||||||
|
|
|||||||||||||||
формулою: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
OS |
= |
S ABC |
=> |
D = S |
|
d |
|
|
B2 |
|
|
|
||||
OD |
|
S ABC |
|
|
|
|
|
|||||||||
|
d |
|
|
|
|
|
|
|
|
|
||||||
|
Приведемо |
|
|
|
приклад |
|
|
|
z |
|||||||
використання точок із площини ABC |
2 |
2 |
|
|||||||||||||
L |
|
K2 |
||||||||||||||
для |
конструювання |
просторових |
T |
|
|
|
||||||||||
|
|
|
|
|||||||||||||
конструкцій.
73
D
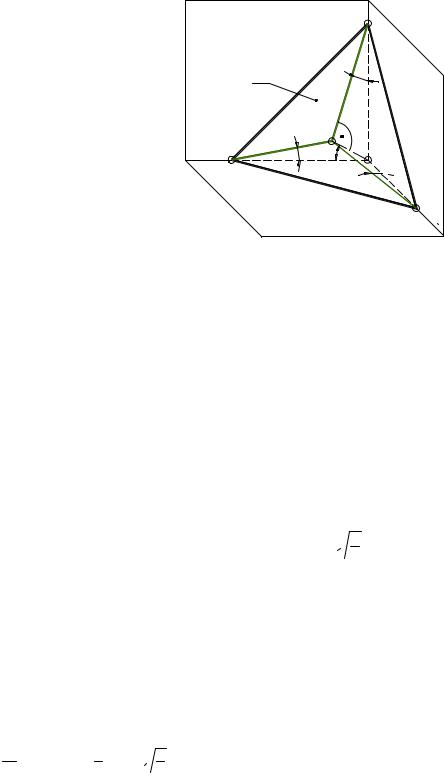
4.8.4. ПОБУДОВА ВЕРШИНИ ТРИКУТНОЇ ПІРАМІДИ ПО ЗАДАНІЙ ОСНОВІ, ВИСОТА ЯКОЇ ПРОЕКТУЄТЬСЯ В ЦЕНТРОЇД ОСНОВИ.
Задача. По заданій основі ABC і висоті h побудувати піраміду ABCK. Висота піраміди проекціюється в центроїд її основи (рис. 4.18).
Графічне розв’язання задачі представлено на рис. 4.18.
Обчислювальний алгоритм
задачі.
h |
|
|
|
A |
|
2 |
|
212 |
f2 |
2 |
|
2 |
2 |
|
|
||
x12 |
C2 |
3 |
|
O S'2 |
D2 |
|
|
|
|
A |
|
|
|
|
|
1 |
|
|
|
|
|
S' |
|
|
|
|
|
1 |
|
T |
|
|
|
f1 |
|
1 |
|
|
|
|
D |
1 |
|
|
11 |
|
|
B |
|
|
|
|
1 |
|
|
|
|
|
21 31
C1
h1 d L L1
0
K0 K1 Рис. 4.18
1.Задано точки: O (0; 0; 0); A (XA; YA; ZA); B (XB; YB; ZB); C (XC; YC; ZC).
2.Обчислимо центроїд (центр ваги) ABC:
T = A + B +C =>
3
X |
T |
= |
1 |
(X |
A |
+ X |
B |
+ X |
C |
) ; |
Y = |
1 |
(Y |
A |
+Y +Y ) ; |
Z |
T |
= |
1 |
(Z |
A |
+ Z |
B |
+ Z |
C |
) . |
|
|
|||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||
|
3 |
|
|
|
|
T |
|
B C |
|
3 |
|
|
|
|
|||||||||||||

74
3. Обчислимо подвійні площі проекцій ABC:
S yz |
|
YA |
Z A 1 |
|
S zx |
|
Z A |
X A 1 |
|
S xy |
|
X A |
YA 1 |
|
|||||||
= |
Y Z |
B |
1 |
; |
= |
Z |
B |
X |
B |
1 |
; |
= |
X |
B |
Y 1 |
. |
|||||
ABC |
|
B |
|
|
ABC |
|
|
|
|
ABC |
|
|
B |
|
|||||||
|
|
YC |
ZC |
1 |
|
|
|
ZC |
X C |
1 |
|
|
|
X C |
YC |
1 |
|
||||
4. Визначимо подвійну площу ABC, розташованого в площині загального положення.
S ABC =  (S ABCyz )2 + (S ABCzx )2 + (S ABCxy )2 .
(S ABCyz )2 + (S ABCzx )2 + (S ABCxy )2 .
Будуємо точку S′ замість S, координати якої взяту в масштабі (1:100) 5. Знайдемо точку виходу з площини на висоту d:
D = ±S |
SABC |
( Задача має два розв’язки. Тому вибирають або “+” або “-” так, щоб |
|||||||
|
d |
||||||||
координати відповідали графічному рішенню) => |
X D = ±X S |
SABC |
; |
||||||
|
|||||||||
|
|
|
|
|
|
|
|
d |
|
YD = ±YS |
SABC |
; |
|
ZD = ±ZS |
SABC |
. |
|
|
|
d |
|
d |
|
|
|
||||
|
|
|
|
|
|
|
|
||
6. Обчислимо координати шуканої вершини K: |
|
|
|
||||||
K=A+D |
|
=> XK=XA+XD; |
YK=YA+YD; |
ZK=ZA+ZD |
|||||
|
Підводячи підсумок, |
відзначимо, що |
метричний |
оператор трьох точок |
|||||
споріднений скалярному добуткові векторів; об’єм піраміди – змішаному добуткові трьох векторів; точка виходу з площини – векторному добуткові двох векторів.
Векторний добуток визначає точку поза площиною – точку виходу з площини, утвореної трьома заданими точками – розширення симплекса, що означає розширення розмірності простору. Скалярний добуток споріднений з метричним оператором точкового числення. Цим визначено число, що характеризує відстань між точками і число, що характеризує кут між орієнтованими відрізками.

75
РОЗДІЛ 5. ТЕОРЕТИЧНІ ОСНОВИ АКСОНОМЕТРІЇ
5.1Основні поняття аксонометрії.
5.2Основні теореми аксонометрії.
5.3Види аксонометрії.
5.4Приведені показники спотворення. Стандартні види аксонометрії.
5.5Координатний спосіб побудови аксонометрії.
5.1. ОСНОВНІ ПОНЯТТЯ АКСОНОМЕТРІЇ
У багатьох випадках при виконанні технічних креслень виявляється необхідним поряд із зображенням предметів у системі ортогональних проекцій мати зображення більш наочні. Для побудови таких зображень застосовують проекції, які названі аксонометричними або, скорочено, аксонометрією. Назва “аксонометрія” утворена зі слів давньогрецької мови: аксон
– вісь і метрео – вимірюю.
Сутність методу паралельного аксонометричного проектування полягає в тому, що предмет відносять до деякої системи координат і потім проектують його паралельними променями на площину разом з координатною системою.
Отже, аксонометрична проекція є, насамперед, проекція тільки на одній площині.
Розглянемо |
|
схему проектування |
|
|
|
|
|
|
|
||||||
точки A на деяку площину α, прийняту за |
|
|
|
|
|
|
|
||||||||
площину |
|
аксонометричних |
|
проекцій |
|
|
|
|
|
|
z' |
||||
(названу |
також |
картинною |
|
площиною). |
|
|
|
|
|
|
α |
||||
|
|
|
|
|
|
|
A' |
||||||||
Напрямок |
проектування |
|
зазначений |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
стрілкою. |
|
|
|
|
|
|
|
|
|
|
|
z |
|
l'z |
|
Прямі Ox, Oy, Oz зображують осі |
|
|
|
|
x' |
||||||||||
|
|
|
|
|
l'x |
||||||||||
координат |
у просторі, |
прямі |
O’x’, O’y’, |
|
|
|
A |
|
A'x |
O' |
|||||
|
|
|
|
|
|
||||||||||
O’z’ – їх проекції на площину α, названі |
|
|
|
|
|
|
l'y |
||||||||
|
|
|
|
|
|
|
|||||||||
аксонометричними |
осями |
(або |
осями |
|
|
|
|
l |
O |
A'1 |
|||||
аксонометричних координат). |
|
|
|
|
|
|
|
|
|||||||
|
|
x |
Ax |
|
l |
|
|
y' |
|||||||
На осях x, y, z відкладений деякий |
|
l |
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||
відрізок |
довжиною |
l, |
прийнятий за |
|
|
|
A1 |
|
|
|
|||||
одиницю |
виміру по |
цих |
осях |
(натуральна |
|
|
|
|
|
|
|||||
|
|
S |
ϕ |
|
y |
|
|||||||||
одиниця). Відрізки l’x, l’y, l’z на |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
аксонометричних |
осях |
являють |
собою |
|
|
|
|
|
Рис. 5.1 |
|
|||||
проекції відрізка l; вони взагалі не рівні l і |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
не рівні між собою. Відрізки l’x, l’y, l’z є
одиницями виміру по аксонометричних осях – аксонометричними одиницями.
l 'x l 'y l 'z
Відношення l , l , l називаються коефіцієнтами спотворення (або
показниками спотворення) по аксонометричних осях.

76
Коефіцієнт спотворення по осі O’x’ позначимо u = ll'x , по осі O’y’ позначимо
v = l 'ly , по осі O’z’ – w = ll'z .
Триланкова просторова лінія OAx1A спроектувалась у плоску ламану лінію O’A’xA’1A’ (рис.1). Точка A’ – аксонометрична проекція точки A; точка A’1 являє собою аксонометричну проекцію точки A1, що є однієї з ортогональних проекцій точки A, а саме на площину П1 (xOy). Точку A’1 називають вторинною проекцією точки A. Можна побудувати ще дві вторинні проекції точки A, що відповідають двом іншим її ортогональним проекціям
– на площинах П2 (xOz) і П3 (yOz).
Відношення між аксонометричними проекціями відрізків прямих ліній, паралельних прямокутним осям координат, і самими відрізками виражаються коефіцієнтами u, v, w.
Кожен з відрізків лінії OAx1A (рис.1) визначає одну з прямокутних координат точки A; проекції цих відрізків – відрізки плоскої ламаної лінії O’A’xA’1A’ визначають відповідно аксонометричні координати тієї ж точки A. Очевидно, за допомогою коефіцієнтів спотворення можна перейти від прямокутних координат до аксонометричних, і навпаки: X’=u, Y’=v, Z’=w, де буквами X’, Y’, Z’ позначені відрізки, що визначають аксонометричні координати точки, а буквами X, Y, Z – відрізки, які визначають її прямокутні координати.
5.2. ОСНОВНІ ТЕОРЕМИ АКСОНОМЕТРІЇ
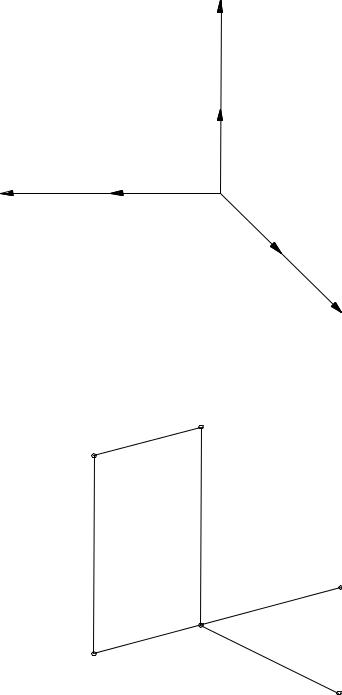
Питання про те, які положення можуть прийняти аксонометричні осі і які величини можуть прийняти аксонометричні одиниці в залежності від положення осей проекцій у просторі і напрямку проектування, було вирішено у другій половині минулого століття геометром Польке. Він довів теорему, сутність якої полягає в наступному.
Нехай ми маємо систему взаємно перпендикулярних площин проекцій OXYZ, на осях якої відкладена натуральна одиниця u
(рис.5.2). Отримана фігура являє собою тетраедр, три взаємно перпендикулярних
ребра якого служать основами масштабів осей проекцій у просторі. Тетраедр OABC
називається масштабним тетраедром. Якщо тепер спроектувати тетраедр OABC на яку-небудь площину ϕ, то одержимо чотирикутник із двома його діагоналями
O’A’B’C’. Напрямки трьох відрізків – O’A’, O’B’ і O’C’ будуть являтися напрямками аксонометричних осей, а величини цих
сторін – основами аксонометричних масштабів (аксонометричними одиницями)
l’x, l’y, l’z.

77
Теорема Польке може бути сформульована так: будь-який чотирикутник зі своїми діагоналями може бути отриманий як паралельна проекція деякого масштабного тетраедра
(рис.5.3).
Ця теорема Польке була узагальнена А. Шварцем. Він довів більш загальну теорему, окремим випадком якої є теорема Польке.
Теорема Польке – Шварца.
Усякий плоский чотирикутник разом з його діагоналями може бути отриманий як паралельна проекція деякого тетраедра, подібного будь-якому даному тетраедрові (рис.5.3).
Рис. 5.3
5.3. ВИДИ АКСОНОМЕТРІЇ
На підставі теореми Польке – Шварца аксонометричні осі і коефіцієнти спотворення по них можуть вибиратися довільно. При цьому коефіцієнти спотворення по аксонометричних осях можна прийняти: різними для всіх аксонометричних осей (u≠v≠w); однаковими для яких-небудь двох осей (наприклад, u=v); рівними для всіх аксонометричних осей (u=v=w). У першому випадку аксонометричну проекцію називають триметричною, у
другому – діметричною і в третьому – ізометричною 1.
В залежності від кута між напрямком проектування і картинною площиною аксонометрія може бути прямокутною (ортогональною), якщо цей кут прямий; у противному випадку її вважають косокутною.
5.4. ПРИВЕДЕНІ ПОКАЗНИКИ СПОТВОРЕННЯ. СТАНДАРТНІ ВИДИ АКСОНОМЕТРІЇ
Встановлення залежності між коефіцієнтами спотворення і напрямком проектування представляє практичний інтерес.
________________________
1 Давньогрецьке слово “isos” - однаковий; ізометрична проекція – проекція однакових коефіцієнтів спотворення по усіх трьох осях; “di” - подвійний; діметрична проекція – проекція однакових коефіцієнтів спотворення тільки по двох осях; “treis” - три; триметрична проекції різних коефіцієнтів спотворення по усіх трьох осях.
78
5.4.1. ПРЯМОКУТНІ ПРОЕКЦІЇ
Нехай площина аксонометричної проекції перетинає координатні осі в точках X≡X’,
Y≡Y’, Z≡Z’, а площини проекцій по прямих XY, |
|
|
z |
|
|
|||||||||||||||||||
XZ, YZ. Точки X, Y, Z – визначають трикутник, |
|
|
|
|
||||||||||||||||||||
|
П2 |
Z=Z' |
|
|
||||||||||||||||||||
названий трикутником слідів (рис.5.4). |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
Очевидно, XYZ≡ΔХ'У'’. |
|
|
|
|
|
|
|
|
|
|
|
|
z' |
|
|
|||||||||
|
|
Опустимо |
з |
початку |
координат |
O |
|
α |
|
П3 |
||||||||||||||
|
|
|
γ |
|
||||||||||||||||||||
перпендикуляр на площину α. Точка О', у якій |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
цей |
перпендикуляр |
|
перетинає |
площину |
є |
|
|
O' |
|
|
||||||||||||||
прямокутною |
|
проекцією |
точки |
O. |
Відрізки |
|
x' |
O |
|
|||||||||||||||
|
x |
α |
|
|||||||||||||||||||||
O’X’, O’Y’ і О'’ – прямокутні аксонометричні |
X=X' |
β |
|
|||||||||||||||||||||
α1 |
y' |
|||||||||||||||||||||||
проекції відрізків координатних осей OX, OY, |
|
|
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
OZ. |
Трикутники |
|
|
OO’X’, |
|
OO’Y’, |
ОО'’ |
– |
|
П1 |
|
Y=Y' |
||||||||||||
прямокутні, |
відрізки |
O’X’, O’Y’, О'’ |
– |
їх |
|
|
||||||||||||||||||
|
|
|
|
y |
||||||||||||||||||||
катети, а відрізки OX’, OY’, OY’ – гіпотенузи |
|
|
|
|
||||||||||||||||||||
|
|
Рис. 5.4 |
|
|
||||||||||||||||||||
цих трикутників. Звідси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
O' X ' |
= cosα , |
O'Y ' |
= cos β , |
|
O'Z ' |
|
= cosγ , |
|
|
|
|
||||||||||||
|
OX ' |
OY ' |
|
OZ ' |
|
|
|
|
||||||||||||||||
де α, β, γ - кути нахилу осей x, y, z до картинної площини. |
|
|
|
|||||||||||||||||||||
|
|
Тому що |
O' X ' |
|
= u , |
|
O'Y ' |
= v , |
|
O'Z ' |
= w , де u=cosα, v=cosβ, w=cosγ. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
OX ' |
|
|
||||||||||||||||||||
|
|
|
|
OY ' |
OZ ' |
|
|
|||||||||||||||||
Для відрізка OO’ косинуси кутів α1, β1, γ1 (рис.5.4) додатних до кутів α, β і γ – є
направляючими косинусами. Тому cos2α1 + cos2β1 + cos2γ1=1, а тому що α=π / 2 - α1 і т.д.,
де sin2α + sin2β + sin2γ=1, тобто 1 - cos2α + 1 - cos2β + 1 - cos2γ=1, звідки cos2α + cos2β + cos2γ=2. Отже u2 + v2 + w2=2, тобто для прямокутної аксонометричної проекції сума квадратів коефіцієнтів спотворення дорівнює двом.
Ізометрична проекція. У прямокутній ізометричній проекції коефіцієнти спотворення по усіх осях однакові: u2 + v2 + w2=2, тобто 3k 2 = 2, k =  23 ,
23 ,
отже, натуральні коефіцієнти спотворення по осях x, y, z рівні 0,82.
Приведеними показниками спотворення називаються показники спотворення подібно перетворених креслень аксонометрії.
Приведені показники спотворення в прямокутній ізометрії u = v = w = 1. Тоді коефіцієнт m збільшення зображення аксонометричного креслення буде дорівнювати
1:0,82=1,22.
Діметрична проекція. Для прямокутної діметричної проекції характерна рівність коефіцієнтів спотворення по двох осях u = v; коефіцієнт спотворення по третій осі w=½u
(або w=½v). Тому 2k 2 + k42 = 2, k 2 = 89 , k =  89 = 0,94 , тобто коефіцієнт спотворення
89 = 0,94 , тобто коефіцієнт спотворення
по осях х' і z’ дорівнює 0,94, а по осі у'=0,47. Діметричну проекцію, як і ізометрію, будують, як правило, без спотворення по осях х' і z' а по осі у' із спотворенням w=0,5. У цьому випадку

|
|
|
|
|
|
|
79 |
|
коефіцієнт m збільшення лінійних розмірів зображення в порівнянні з дійсними відбувається |
||||||||
в 1:0,94=1,06 рази. |
|
|
|
|
|
|||
|
5.4.2. КОСОКУТНІ ПРОЕКЦІЇ |
|
|
|
||||
|
Залежність між показниками спотворення і напрямком проектування прямокутного |
|||||||
тригранника виражається у виді наступної теореми: у косокутних аксонометричних |
||||||||
проекціях сума квадратів коефіцієнтів спотворення дорівнює 2 + ctg2ϕ, тобто u2 + v2 + w2=2 |
||||||||
+ +ctg2ϕ, де ϕ - кут між напрямком проектування і площиною аксонометричних проекцій |
||||||||
(рис.1). |
|
|
|
|
|
|
||
|
Отже, у косокутній аксонометрії сума квадратів показників спотворення більше 2. |
|||||||
|
На практиці часто застосовують проекції на площини, паралельні площині проекцій |
|||||||
П2, тому що при такій проекції дві осі проекцій, паралельні їм прямі, а також усі прямі і |
||||||||
кути, що лежать у площині П2, проектуються без спотворення. |
|
|
||||||
|
Фронтальні проекції. Нехай осі OX і OZ просторової ортогональної системи |
|||||||
координат розташовані паралельно площинам аксонометричних проекцій. Напрямок |
||||||||
проектування варто вибрати так, щоб проекції координатних осей на площині |
||||||||
розташовувалися, як зазначено на рис.5. При цьому прямий кут між осями OX і OZ, |
||||||||
натуральні масштаби, відкладені на них, спроектуються без спотворення. Третя |
||||||||
аксонометрична вісь O’Y’ розташовується під кутом 45° до горизонталі і |
||||||||
аксонометричному |
масштабу |
надається |
|
Z |
|
|||
значення натурального або половини його. |
П2 |
|
||||||
|
У такий спосіб: |
|
|
|
|
|
||
|
а) якщо показники спотворення u=v=w=1, |
α |
|
|
||||
то |
косокутна |
проекція |
називається |
Z' |
П3 |
|||
|
||||||||
фронтально-ізометричною. Тоді з формули u2 + |
|
|
|
|||||
v2 + w2=2 + ctg2ϕ випливає, що ctg2ϕ=1 і, отже, |
|
X' |
|
|||||
кут ϕ=45°; |
|
|
|
|
|
|||
|
|
|
X |
O' |
|
|||
|
б) якщо показники спотворення u = w = 1, |
O |
Y' |
|||||
а v = 0,5, то косокутна проекція називається |
|
|||||||
фронтально-діметричною. Отже 1 + 0,5 + 1=2 |
|
|
|
|||||
+ +ctg2ϕ, тому ctg2ϕ=0,5 і кут ϕ=63о. |
П1 |
|
Y |
|||||
|
|
|
|
|
|
|
||
|
5.5. |
КООРДИНАТНИЙ |
СПОСІБ |
|
Рис. 5.5 |
|||
|
ПОБУДОВИ АКСОНОМЕТРІЇ |
|
||||||
|
|
|
|
|||||
Робота з побудови аксонометричних проекцій є досить монотонною і трудомісткою, що звичайно приводить до появи технічних помилок. Тому аксонометрична проекція заданого геометричного образу будується по його окремих точках, використовуючи звичайний координатний метод. При цьому доцільно дотримуватися визначеного порядку роботи. Цей порядок може бути різним у деталях, однак загальна схема буде наступною:
1. Зафіксувати на комплексному кресленні просторову систему координат. Найчастіше цю систему координат вибирають таким чином, щоб її осі збігалися з осями симетрії заданого оригіналу.

80
2.Вибрати одну із стандартних аксонометричних проекцій. При цьому доцільно керуватися наступними міркуваннями.
Найбільш простою у застосуванні і достатньо наочною є прямокутна ізометрична проекція. Особливо бажано її застосовувати в тих випадках, коли елементи геометричного об'єкта по всіх трьох взаємно перпендикулярних напрямках представляються однаково важливими, а також коли необхідно побудувати наочне зображення оригіналу, що містить у двох або трьох взаємно перпендикулярних площинах кола. Однак варто пам'ятати, що розглянута аксонометрична проекція дає дуже великий, незвичний для ока нахил, що особливо позначається при зображенні об'єктів призматичної форми, особливо куба. І вона зовсім неприйнятна в тих випадках, коли оригінал містить бісекторні (нахилені під 45° до площин проекцій) площини.
Прямокутну діметричну проекцію доцільно застосовувати в тих випадках, коли важливе зображення елементів оригіналу, що знаходяться на виді спереду, а також у тих випадках, коли зображувана фігура витягнута переважно в одному напрямку.
Що стосується косокутних проекцій, що їх доцільно застосовувати в тих випадках, коли геометричний об'єкт містить перпендикулярні якому-небудь одному з напрямків ряд кіл.
3.Побудувати аксонометричні осі. ДСТ 2.317-69 передбачає, що для будь-якої стандартної аксонометричної проекції вісь z’ розташовується вертикально. Що ж стосується інших аксонометричних осей, то їх положення визначається відповідно до кутів, що вони
складають з віссю z’.
Аксонометричні осі прямокутної ізометричної проекції, що складають між собою кути в 120°, можна побудувати, використовуючи радіус довільної кола, проведеного з початку аксонометричної системи координат O’ (рис. 5.6), або використовуючи значення тангенса кута, рівного 30° і доповнюючого кути між осями до прямих (tg30°≈4/7).
Положення осей х' і у' у прямокутній діметричній проекції зручніше визначати за допомогою тангенсів кутів додатних до прямих кутів (рис.5.7), використовуючи відомі співвідношення:
tg7°10’≈1/8 tg41°25’≈7/8
4.Усвідомити конструктивні особливості заданого геометричного образу і вхідних до нього елементів.
5.Побудувати аксонометричні проекції вхідних у геометричний образ елементів.
6.Виконати оформлення аксонометричної проекції (провести окреслювальні лінії, обвести лінії видимого контуру і т.д.).
z'
7 |
O' |
4 |
|
|
>4:7 |
x' |
y' |
Рис. 5.6
z'
x' |
|
O' |
tg7°10'≈1/8 |
tg41°25'≈7/8 |
|
|
|
Рис. 5.7
y'
