
Спецкурс численные методы.
...pdf
41
|
1 |
|
|
|
|
0.3cosx |
|
0.3; |
1 |
|
|
|
0.373sin x |
|
|
0.373; |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
x1 |
x2 |
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
0.4sin x |
|
0.4; |
|
|
|
2 |
|
|
|
|
|
|
0.17cosx |
|
0.17 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x1 |
x2 |
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, l |
|
|
M |
|
|
|
max (0.3 0.4 ;(0.373 0.17)) 0.7 1. |
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
Итак, применение метода простых итераций возможно.
Условие выхода из цикла (x(n) ,x(n 1) ) 1 l 1.0 0.70.005 0.00214 l 0.7
3. Назначим начальное приближение (трудоёмкие прикидки отвлекли бы нас от основной идеи лекции, поэтому опущены): x1(0) 0.4; x2(0) 0.2.
4. Организуем модифицированный итерационный цикл
x1(1) 0.3sin0.4 0.373cos0.2 0.482; x2(1) 0.4cos0.482 0.17sin0.2 0.321;
(x(1) ,x(0) ) max(0.482 0.400; 0.321 0.2) 0.121 0.00214;
x1(2) 0.3sin0.482 0.373cos0.321 0.493; x2(2) 0.4cos0.493 0.17sin0.321 0.299;
(x(2) ,x(1) ) max(0.493 0.482; 0.299 0.321) 0.022 0.00214;
x1(3) 0.3sin0.493 0.373cos0.299 0.498; x2(3) 0.4cos0.498 0.17sin0.299 0.301;
(x(3) ,x(2) ) max(0.498 0.493; 0.301 0.2.99) 0.005 0.00214;
x1(4) 0.3sin0.498 0.373cos0.301 0.500; x2(4) 0.4cos0.500 0.17sin0.301 0.301;
(x(4) ,x(3) ) max(0.500 0.498; 0.301 0.2301) 0.002 0.00214.
Следовательно, решение x1 0.500, x2 0.301 с погрешностью, не превышающей допустимую величину, приближает точное решение.
4.3. Критерии усвоения
После изучения содержания данной темы Вы должны:
знать
как решаются методом простых итераций нелинейные уравнения и системы нелинейных уравнений;
каким условиям должны удовлетворять уравнения для того, чтобы их можно было решать методомпростых итераций;
42
как контролируется погрешность очередной итерации;
понимать
роль каждого условия применения метода;
смысл алгоритма решения на каждой итерации;
Уметь
применять метод простых итераций для решения нелинейных уравнений и их систем.
4.4. Выход темы в другие темы и дисциплины
Данная тема имеет выход в дипломные, магистерские и диссертационные работы.
4.5.Тест - контроль для самопроверки
4.1.Что называется линеаризацией нелинейной задачи?
А. Следующая последовательность процедур:
1.Проверка выполнения условий применения данной итерационной схемы.
2.Разделение корней (выделение подобластей, включающих единственный корень) и выбор нулевых приближений для каждой подобласти..
3.Выполнение итераций, включающих
-формулирование линейной задачи i- ой итерации;
-решение этой задачи с использованием результатов предыдущей итерации
(предыдущих итераций);
-проверка условий выхода из итерационного цикла;
-при выполнении указанных условий – выход из цикла. Б. Формулирование линейной задачи i- ой итерации.
В. Формулирование и решение линейной задачи i- ой итерации с использованием
результатов предыдущей итерации (предыдущих итераций).
Г. Преобразование нелинейной задачи в линейную задачу. 4.2. Что называется неподвижной точкой оператора?
А. Наименьшее из таких чисел C 0, для которых выполняется условие
|
Az |
C |
|
z |
|
z E, |
|
|||||||||||
где |
|
|
|
z |
|
|
|
|
и |
|
|
|
Az |
|
- нормы элемента z и его образа Az. |
A - заданный оператор, - |
||
|
|
|
|
|
|
|
||||||||||||
Б. |
|
|
|
Элемент z, |
удовлетворяющий условию Az , где |
|||||||||||||
нулевой элемент.
В. Элемент x* X , удовлетворяющий условию Ax* x*.
Г. Элемент y.такой, что 
 Ay
Ay
 min
min 
 Ax
Ax
 , где A - заданный оператор.
, где A - заданный оператор.
x D(A)
4.3. Что такое область сходимости неподвижной точки оператора A?
А. Область S , если для каждой точки x Sсуществует элемент Ax.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
Б. |
Область S , |
если для каждой точки y S можно указать такой элемент x, |
что |
|||||||||||||||||||||||||||||||||||||||||||
Ax y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В. Множество всех элементов N(A,x*) такое, что для любого x(0) |
N(A,x*) |
|
||||||||||||||||||||||||||||||||||||||||||||
последовательность x(0) , x(1) |
Ax(0) , |
x(2) Ax(1) ,..., x(n) Ax(n 1) ,... принадлежит ей. |
|
|||||||||||||||||||||||||||||||||||||||||||
Г. Множество всех элементов N(A,x*) такое, что для любого x(0) |
N(A,x*) |
|
||||||||||||||||||||||||||||||||||||||||||||
последовательность x(0) , x(1) |
Ax(0) , |
x(2) Ax(1) ,..., x(n) Ax(n 1) ,... сходится к x*. |
|
|||||||||||||||||||||||||||||||||||||||||||
4.4. Что называется оператором сжатия? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
А. |
Оператор |
A, |
удовлетворяющий условию |
Ax , где |
x D(A), |
|
|
- нулевой |
||||||||||||||||||||||||||||||||||||||
элемент. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б. |
Оператор A, удовлетворяющий условию |
|
|
|
Ax |
|
|
|
|
|
|
|
Ay |
|
|
|
, если |
|
|
|
|
x |
|
|
|
|
|
|
|
|
y |
|
|
|
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
В. |
Оператор |
A: X X , |
для которого можно указать постоянную l (0;1) такую, |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
что (Ax ,Ax ) l (x ,x ) |
x |
,x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Г. |
|
Оператор |
|
A: X X , |
для которого можно указать постоянную |
|
l |
такую, |
что |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(Ax ,Ax |
|
) l (x |
,x ) |
x ,x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4.5. Что называется методом простых итераций?
А. Следующая последовательность вычислительных процедур.
1.Проверка возможности использования метода.
2.Выбор начальной точки.
3.Последовательное выполнение итераций, причём любая i- ая итерация выполняется по формуле x(i) Ax(i 1) .
4.Условия выхода из цикла могут иметь следующий вид:
ln |
(x(1) ,x(0) ) , |
|||
1 l |
||||
|
(1 l) |
|
||
n ln |
, |
|||
(x(1) ,x(0) ) |
||||
|
|
|
||
(x(n) , x(n 1) ) 1 l .
l
Б. Следующая последовательность вычислительных процедур:
1.Проверка возможности использования метода.
2.Выбор начальной точки.
3.Последовательное выполнение итераций, причём любая i- ая итерация выполняется по формуле x(i) Ax(i 1) .
4.Условия выхода из цикла могут иметь следующий вид:
li |
(x(i) ,x(i 1) ) , |
|
1 l

44
(1 l) n ln (x() , x(0) ) ,
(x(n) , x(n 1) ) 1 l .
l
В. Следующая последовательность вычислительных процедур:
1.Проверка возможности использования метода.
2.Выбор начальной точки.
3.Последовательное выполнение итераций, причём любая i- ая итерация выполняется по формуле x(i) Ax(i 2) .
4.Условия выхода из цикла могут иметь следующий вид:
li |
(x(i) ,x(i 1) ) , |
|
1 l |
||
|
(1 l) n ln (x() , x(0) ) ,
(x(n) , x(n 1) ) 1 l .
l
Г. Следующая последовательность вычислительных процедур:
1.Проверка возможности использования метода.
2.Выбор начальной точки.
3.Последовательное выполнение итераций, причём любая i- ая итерация выполняется по формуле x(i) Ax(i 1) .
4.Условия выхода из цикла могут иметь следующий вид:
li |
(x(i) ,x(i 1) ) , |
|
1 l |
||
|
(1 l) n ln (x() , x(0) ) ,
(x(n) , x(n 1) ) 1 l .
l

45
Ответы на тест – контроль 4.1-«А» Следующая последовательность процедур:
1.Проверка выполнения условий применения данной итерационной схемы.
2.Разделение корней (выделение подобластей, включающих единственный корень)
ивыбор нулевых приближений для каждой подобласти..
3.Выполнение итераций, включающих
-формулирование линейной задачи i- ой итерации;
-решение этой задачи с использованием результатов предыдущей итерации
(предыдущих итераций);
-проверка условий выхода из итерационного цикла;
-при выполнении указанных условий – выход из цикла.
4.2- «В» Элемент x* X , удовлетворяющий условию Ax* x*. |
|
||||||
4.3.- «В» Множество всех элементов N(A,x*) такое, что для любого x(0) |
|
||||||
N(A,x*) последовательность x(0) , x(1) |
Ax(0) , x(2) Ax(1) ,..., x(n) Ax(n 1) ,... |
|
|||||
принадлежит ей. |
|
A: X X , для которого можно указать постоянную |
l (0;1) |
||||
4.4- В. Оператор |
|||||||
|
|
|
|
|
|
X . |
|
такую, что (Ax ,Ax |
) l (x ,x |
) x ,x |
|
|
|||
4.5- А. Следующая последовательность вычислительных процедур.
1.Проверка возможности использования метода.
2.Выбор начальной точки.
3.Последовательное выполнение итераций, причём любая i- ая итерация выполняется по формуле x(i) Ax(i 1) .
4.Условия выхода из цикла могут иметь следующий вид:
ln |
(x(1) ,x(0) ) , |
|||
1 l |
||||
|
(1 l) |
|
||
n ln |
, |
|||
(x(1) ,x(0) ) |
||||
|
|
|
||
(x(n) , x(n 1) ) 1 l .
l
46
ЧМ-5. МЕТОД НЬЮТОНА. МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА. МЕТОД СЕКУЩИХ
5.1. Входная информация для самопроверки
Для изучения данной темы Вам необходимо восстановить в памяти:
- из курса прикладной математики - понятия линейной алгебры, числовой последовательности, функциональной последовательности, предела, производной, касательной, степенного ряда;
- из настоящего спецкурса - понятия: пространства, оператора, функционала, линейного оператора.
5.2. Содержание темы
Для решения нелинейного операторного уравнения методом простых итераций это уравнение должно иметь определённый вид. Более широкие возможности предоставляет метод Ньютона, или метод касательных, а также некоторые родственные ему методы (модифицированный, или упрощенный, метод Ньютона, усиленный метод Ньютона, метод секущих).
В операторном представлении уравнения, которые решаются этим методом, выглядят
так
A(x) , |
(5.1) |
где A(.): E E |
- оператор, в общем случае, нелинейный; E - нормированное |
пространство; x E ; - нулевой элемент этого пространства.
Для нас требование, чтобы оператор действовал из нормированного пространства в нормированное пространство, не является обременительным, так как состояние рассчитываемых объектов описывается только скалярами, векторами или функциями, а соответствующие пространства (R, Rn , L2 ), как мы видели, - нормированные.
Мы будем решать такие уравнения, заданные в функциональных пространствах, а именно, одно нелинейное уравнение (неизвестное - число x) и систему нелинейных уравнений (неизвестен вектор x (x1,x2 ,...,xn ), где n - порядок системы). Такие уравнения имеют вид:
в случае одного нелинейного уравнения - |
|
f (x) 0, |
(5.2) |
в случае системы нелинейных уравнений - |
|
f1(x1,x2 ,...,xn ) 0, |
|
f2 (x1,x2 ,...,xn ) 0, |
|
............................... |
(5.3) |
................................ |
|
fn (x1,x2 ,...,xn ) 0, |
|
|
|
|
|
47 |
где |
f (x), f1(x1,x2 ,...,xn ), f2 (x1,x2 ,...,xn ),..., fn (x1,x2 ,...,xn ) |
- |
числовые |
функции |
действительных аргументов (одного аргумента x или нескольких аргументов x1,x2,...,xn ).
Система (5.3) может быть записана более компактно в векторных обозначениях
F(x) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.3а) |
||
где F(x) ( f |
1 |
(x ,x |
2 |
,..., x |
n |
), f |
2 |
(x ,x |
2 |
,..., x |
n |
),..., f |
n |
(x ,x |
2 |
,..., x |
n |
))T Cn[a,b] - n-мерная вектор- |
|
1 |
|
|
1 |
|
|
1 |
|
2 |
|||||||||
функция n аргументов; мерный нуль-вектор. |
|
|
|
|
|
|
||||||||||||
Эта группа методов наиболее часто применяется при решении нелинейных задач |
||||||||||||||||||
строительной механики. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Применение метода Ньютона предполагает выполнение некоторых условий, налагаемых на функции в левой части уравнений (5.2) и (5.3), а также на область, в которой предполагается осуществлять поиск корня (корней) этих уравнений. Совокупность этих условий достаточна для реализуемости метода. В любом случае выделяется подобласть, в которой находится только одно решение (один корень в случае одного уравнения и один вектор в случае системы уравнений). Этому соответствует одна перемена знака функции (функций) в пределах указанной подобласти. Указанные функции должны быть
непрерывными |
вместе |
со |
своими |
первыми |
и |
вторыми |
производными |
( f (x) C2[a,b], F(x) C2n[B]; |
[a,b], [B]- подобласти |
поиска), |
причём |
эти производные |
|||
должны сохранять знак в пределах той же подобласти. Очень важное, но трудно контролируемое, условие - начальное приближение (см. лекцию ЧМ-4) должно быть достаточно близко к точному решению (которое , естественно, неизвестно).
Рассмотрим вначале применение метода Ньютона для решения одного уравнения (5.2). В этом случае условия, обеспечивающие возможность реализации этого метода и сходимость последовательности решений выглядят так:
f (x) C2[a,b] ; |
|
|
|
|
|
|
|
(5.4) |
||
sign f |
|
(x) const; |
x [a,b]; |
|
|
|
|
|
(5.5) |
|
|
|
|
|
|
|
|||||
f (a) f (b) 0; |
|
|
|
|
|
|
|
(5.6) |
||
sign f |
|
|
|
|
|
|
2 |
x [a,b]; |
(5.7) |
|
|
|
|
||||||||
|
(x) const; |
|
f (x) f (x) |
|
( f (x)) |
|
||||
|
|
|
|
|
|
|
|
|
|
(5.8) |
f (x) 0; f (x) 0; f (x) A x [a,b]; |
||||||||||
(x0 ,x*) a |
|
|
|
|
|
|
|
(5.9) |
||
f (x0) f (x0) 0; |
|
|
|
|
|
|
|
(5.10) |
||
В (5.9) |
x* -корень уравнения (5.2), |
a 0-достаточно малая величина. |
|
|||||||
Условие (5.4) гарантирует наличие первой производной, которая используется в процессе вычислений, а также наличие непрерывной второй производной, что необходимо (но не достаточно) для обеспечения сходимости последовательности решений. Условия (5.5)
и(5.6) обеспечивают единственность корня на заданной области. Выполнение условий (5.7)
и(5.8) достаточно для обеспечения сходимости (при выполнении остальных условий). Неравенства (5.9) и (5.10) задают условия для выбора начальной точки.
Схема метода Ньютона для решения одного нелинейного уравнения (5.2) соответствует общей идее итерационных методов, описанной в лекции ЧМ-4, и выглядит следующим образом.
48
Подготовительный этап. Выполняется проверка возможности использования метода и разделение корней. Без него метод может не работать (произойдёт зацикливание или последовательность решений будет расходящейся).
Это наименее формализованная, основанная на интуиции часть расчёта. Она заключается в том, что по виду уравнения проверяется его соответствие требованию (5.4) и определяются (возможно, достаточно грубо) приближённые значения всех корней, после чего вся заданная область поиска корней разбивается на подобласти, в каждой из которых находится один и только один корень. Поведение функции f (x) уравнения (5.2) в пределах каждой подобласти должно удовлетворять условиям (5.5)-(5.8). При этом каждая подобласть будет принадлежать области сходимости лежащего в ней корня.
Первый этап. В каждой из подобластей, полученных на первом этапе, выбирается начальное приближение, сообразуясь с условием (5.9). Для его выбора может быть использован, например, графический метод, то есть, строится график функции, заданной левой частью уравнения (5.2), и определяются абсциссы его пересечения с осью Ox, которые и принимаются за грубые оценки корней и подходящие точки для начальных приближений. Для этих начальных точек проверяется выполнение условия (5.10). Если это последнее условие не выполняется, метод без серьёзной корректировки не может быть применён.
Второй этап. Выполняется требуемое число раз определение приближённого решения (с использования полученного на предыдущем приближении решения) и сравнение
оценки погрешности очередного приближённого решения с допустимой величиной погрешности (см. лекцию ЧМ-1).
По результатам этого сравнения принимается решение о продолжении процесса или о выходе из итерационного цикла.
В методе Ньютона поиск приближённого решения выполняется следующим образом.
На каждой i- |
той итерации (i 1;2;...) функция |
f (x) |
аппроксимируется линейной |
||||||||||
функцией |
|
|
|
|
|
|
|
|
|
|
|
|
|
~(i) |
(x) f (x |
(i 1) |
) k |
(i) |
(x x |
(i 1) |
). |
|
|
(5.11) |
|||
f |
|
|
|
|
|
|
|
||||||
Очевидно, что для |
первого |
приближения |
i 1, x(i 1) x(0) . Если функция |
||||||||||
f (x) C , можно считать, что |
f (x) аппроксимируется конечным (двучленным) отрезком |
||||||||||||
ряда Тейлора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Угловой коэффициент аппроксимации принимается из условия, что график |
|||||||||||||
аппроксимации совпадает с касательной к графику функции |
f (x) в точке, совпадающей |
||||||||||||
предыдущим корнем, |
то-есть, |
k |
(i) |
f |
|
|
(i 1) |
). Это соответствует коэффициенту при первой |
|||||
|
(x |
|
|
||||||||||
степени приращения аргумента в ряде Тейлора (когда f (x) C ). На этом основании метод Ньютона называют также методом касательных (рис. 5.1).
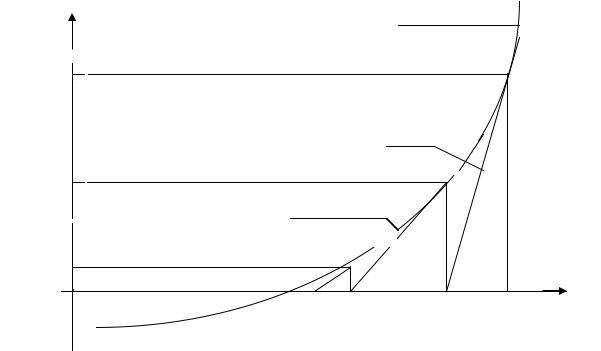
|
|
|
49 |
f (x) |
|
y f (x) |
|
|
|
|
|
f (x(0) ) |
|
|
|
|
|
y ~f (1) (x) |
|
f (x(1) ) |
|
|
|
y ~f (2) (x) |
|
|
|
f (x(2) ) |
|
|
x |
x(3) |
x(2) |
x(1) |
x(0) |
Рис. 5.1. |
|
|
|
В качестве приближённого значения искомого корня на i |
- ой итерации принимается |
||
корень аппроксимации на этой итерации: |
|
|
|
~(i) |
(x) f (x |
(i 1) |
) k |
(i) |
(x x |
(i 1) |
) 0,. |
(5.12) |
|||||||||||
f |
|
|
|
|
|
||||||||||||||
откуда |
|
|
|
|
f (x(i 1) ) |
|
|
|
|
|
f (x(i 1) ) |
|
|||||||
x |
(i) |
x |
(i 1) |
|
x |
(i 1) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
(5.13) |
|||||||
|
|
|
k |
(i) |
|
f |
|
(i 1) |
) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
|
|
|
|||
Условие (5.8) как раз и обеспечивает возможность выполнения вычислений по формуле (5.13).
Как следует из (5.13), алгоритм метода Ньютона для уравнения (5.2) соответствует алгоритму метода простых итераций для уравнения
x g(x), |
(5.14) |
||
где |
|
||
g(x) x |
f (x) |
. |
(5.15) |
|
|||
f (x)
Как было определено в лекции ЧМ-4, условие сходимости метода простых итераций для уравнения (5.15) имеет вид

50
|
|
|
f |
|
(x) |
2 |
|
f (x) f |
|
|
f (x) f |
|
|
|
|
|||
|
|
1 |
|
|
(x) |
|
(x) |
1, |
(5.16) |
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
||||||
g (x) |
|
|
( f |
|
|
|
|
|||||||||||
|
|
|
|
|
(x)) |
|
|
|
( f |
(x)) |
|
|
|
|||||
что и даёт второе условие (5.7).
Известны оценки погрешности очередного n- го приближения
|
x* x(n) |
|
|
|
|
|
|
M1 |
|
|
|
x(n 1) x(n) |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.17) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
x* x(n) |
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
x* x(n) |
|
|
|
m1 |
|
|
|
x* x(0) |
|
|
|
m1 |
)n (b a), |
|
||||||||||||||||||||
|
|
|
|
(1 |
) |
|
|
(1 |
)n |
|
|
(1 |
(5.18) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
M1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x* x(n) |
|
|
2m1 |
|
|
( |
|
|
M2 |
(x* x(0) ))2n |
|
2m1 |
( |
M2 |
(b a))2n |
, |
|
|
(5.18) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
|
2m1 |
|
|
M2 |
|
|
|
2m1 |
|
|
|
|
|
|
|||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
f (x*) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
m1 |
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.19) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
M1 |
|
x x0 ,x* |
|
|
|
f (x) |
|
|
|
|
|
f (x0 ) |
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.20) |
|||||||||||||||||||||||
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
M2 |
|
x x0 ,x* |
|
f (x) |
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.21) |
|||||||||||||||||||||||||||||||||
|
|
|
x a0 ,b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x* - точное (неизвестное) значение корня уравнения (5.2). Перейдём к решению системы нелинейных уравнений (5.3).
Подготовительный этап также плохо формализован. Проверяется условие
F(x*) C2n (B), |
(5.22) |
где B - область, где разыскиваются решения. Затем выделяются подобласти |
с одним |
решением в каждой и по возможности локализуются точки x*, где F(x*) . |
|
Первый этап аналогичен случаю одного уравнения – выбираем начальное приближение в каждой подобласти.
Второй этап также состоит в многократном решении аппроксимирующего линейного уравнения, только теперь – векторно-матричного, то-есть, системы аппроксимирующих линейных уравнений. Повторяя рассуждения, аналогичные случаю одного уравнения,
запишем |
аппроксимирующее вектор-функцию F(x) выражение (линейное относительно |
|||||||||||||
(x |
j |
x(i 1) |
) и имеющее первые частные производные в точке x(i 1) |
(x(i 1) |
,x(i 1) |
,...,x(i 1) ), |
||||||||
|
j |
|
|
|
|
|
|
|
|
|
1 |
2 |
n |
|
равные одноимённым производным заданных функций) в виде |
|
|
|
|||||||||||
|
|
~ |
(i) |
|
(i 1) |
|
F (i 1) |
|
(i 1) |
|
|
|
|
|
|
|
F |
|
(x) F(x |
|
) |
|
|
(x x |
|
), |
|
|
(5.23) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
