FIZIKA_kospekt_lektsy

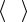
Учитывая действующие значения тока и напряжения, выражение средней мощности (21.37) можно записать в виде

где множитель cosφ называется коэффициентом мощности.

Формула (21.38) показывает, что мощность, выделяемая в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи реактивное сопротивление отсутствует, то cosφ = 1 и N = IU. Если цепь содержит только реактивное сопротивление (R = 0), то cos φ= 0 и средняя мощность равна нулю, какими бы большими ни были ток и напряжение.

Если cosφ имеет значения, существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приведет либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить cosφ, наименьшее допустимое значение которого для промышленных установок составляет примерно 0,85.

221

ГЛАВА 22. УПРУГИЕ ВОЛНЫ

22.1.Волновые процессы. Продольные и поперечные волны

Колебания, распространяющиеся в упругой среде с конечной скоростью,

называются волнами.

При распространении волны, частицы среды не движутся вместе с волной, а колеблются около своего положения равновесия. Вместе с волной от частицы к частице передается состояние колебательного движения и его энергии без переноса вещества.

Типы волн:

Упругие волны.

Электромагнитные волны.

Упругие волны – механические возмущения, распространяющиеся в упругой среде.

Волны бывают продольные и поперечные:

Продольные волны – когда частицы среды колеблются в направлении распространения волны. В данном случае создаются чередующие сгущения и разряжение среды. Продольные волны возникают за счет деформации смещения в твердых телах, жидкостях и газах.

Поперечные волны – когда частицы колеблются в плоскости перпендикулярной распространению волны. Поперечные волны возникают за счет деформации сдвига в твердых телах.

Упругая волна называется гармонической, когда соответствующие ей колебания частиц среды являются гармоническими. На рис.21.1. представлена гармоническая поперечная волна распространяющейся со скоростью υ вдоль оси х, т.е. приведена зависимость смещения ξ частиц среды, участвующих в волновом процессе и расстоянием х этих частиц от источника колебаний для какого-то фиксированного момента времени t (например частицы В, показанной на рис. 22.1).

222

Хотя приведенный график функции ξ(x,t) похож на график гармонического колебания, но они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний х в данный момент времени, а график колебаний (см. рис.19.1.) –

зависимость смещения данной частицы от времени.

Наименьшее расстояние между частицами, колеблющимися в одной фазе,

называется длиной волны λ (рис.22.1). Длина волны равна расстоянию, на которое распространяется фаза колебаний за один период т.е.

При волновом процессе колеблются не только частицы вдоль оси, а

совокупность частиц расположенных в некотором объеме, т.о. волна распространяясь от источника колебаний охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t называется волновым фронтом.

Геометрическое место точек колеблющихся в одной фазе называется волновой поверхностью. Волновых поверхностей можно провести множество, а

волновой фронт в каждый момент времени – один. Волновые поверхности могут быть любой формы. В простейшем случае они представляют собой совокупность плоскостей параллельных друг другу или совокупность концентрических сфер. В зависимости от волновой поверхности волны делятся

на плоские и сферические.

223

22.2.Уравнение бегущей волны

Бегущими волнами называются воны, которые переносят в пространстве энергию. Перенос энергии в волнах количественно характеризуется вектором плотности потока энергии. Это вектор для упругих волн называется вектором Умова J .Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии переносимой волной за единицу времени через единицу площади, расположенную перпендикулярно распространению волны.

Плотность потока энергии W , где V- объем.

V

где ρ – плотность среды.

Для вывода уравнения бегущей волны – зависимости смещения колеблющейся частицы от координат x и времени t – рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с распространением волны. Волновые поверхности перпендикулярны оси х, а также все точки волновой поверхности перпендикулярны оси х, а так

как все точки волновой поверхности колеблются одинаково, то смещение будет зависеть только от x и t.

На рис.22.1 рассмотрим некоторую частицу среды В, находящуюся от источника колебаний на расстоянии х. Если колебания точек лежащих в плоскости х=0, описывается функцией (0,t) Acos t, то частица среды В колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на τ, так как для прохождения волной расстояния х

требуется время x , где υ- скорость распространения волны. Тогда

уравнение колебаний частиц, лежащих в плоскости х, имеет вид:

224

где (x,t) - является периодической функцией времени и координаты;

x/υ – время, когда начала колебаться точка В.

Уравнение (22.4) есть уравнение бегущей волны. Если же плоская волна распространяется в противоположном направлении от источника колебаний уравнение представлено в виде:

В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления х в среде, не поглощающей энергию, имеет вид.

где А=const амплитуда волны, ω – циклическая частота волны, φ0 – начальная фаза колебаний, определяемая в общем случае выбором начала отсчета x и t,

Уравнение распространяющейся вдоль отрицательного направления оси

х, отличается от (22.8) только знаком перед коэффициентом kx.

Продифференцировав выражение (22.9), и сократив на ω получим

dt 1dx 0.

Откуда

где υ – скорость распространения волны в уравнении (22.10) есть скорость

перемещения фазы волны и называется фазовой скоростью.

Если фазовая скорость волн в среде зависит от их частоты, то это явление называют дисперсией волн.

Аналогичными рассуждениями выведем уравнение сферической волны – волны, волновые поверхности которой имеют вид концентрических сфер:

где r –расстояние от центра волны до рассматриваемой точки среды.

В случае сферической волны, даже в среде не поглощающей энергию амплитуда колебаний не остается постоянной, а изменятся по закону 1/r.

Уравнение (22.11) справедливо лишь для r значительно превышающих размеры источника (тогда источник колебаний можно считать точечным).

Распространение волн в однородной изотропной среде в общем случае записывается волновым уравнением- дифференциальным уравнением в частных производных:

где υ – фазовая скорость,

Тогда уравнение (22.12) можно записать

226

Решением уравнения (22.12) является уравнение любой волны (плоской или сферической). Соответствующей подстановкой моно убедиться что уравнению (22.13) удовлетворяют решения для плоской волны (22.8) или

(22.11) для сферической волны. Для плоской волны, распространяющейся вдоль оси х, волновое уравнение принимает вид:

22.4.Принцип суперпозиции волн. Групповая скорость

Если среда в которой распространяется одновременно несколько волн,

линейна, т.е. свойства не изменяются под действием возмущений, создаваемых волной, то к ним применим принцип суперпозиции (наложения) волн. При распространении в линейной среде нескольких волн, каждая из них распространяется, как будто другие волны отсутствуют, а результирующее смещение частицы среды равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагаемых волновых процессов.

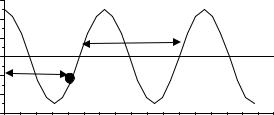
Любая волна может быть представлена в виде суммы гармонических волн и т.е. в виде волнового пакета, или группа волн как показано на рис. 22.2.

Волновым пакетом – называется суперпозиция волн отличающихся друг от друга по частоте и занимающая в каждый момент времени ограниченную область пространства.

х

х

Рис.22.2.

Рассмотрим простейший волновой пакет из двух распространяющихся вдоль положительного направления волн. С одинаковыми амплитудами А0,

227

которые отличающиеся по частоте и +d причем d << , и волновыми числами k и k+dk при условии, что dk<<k

(x,t) A0 cos( t kx) A0 cos( d )t (k dk)x)

За скорость распространения этого волнового пакета принимают перемещение максимума амплитуды (точка C на рис.22.2), рассматривая его в

где u – групповая скорость

Cвязь между групповой u и фазовой υ скоростями дается соотношением:

Групповая скорость может быть больше или меньше фазовой это зависит от знака dυ/dλ.

Понятие групповой скорости очень важно, так как именно она фигурирует при измерении дальности радиолокации в системах управления космическими объектами. В теории относительности доказывается, что групповая скорость u c в то время как для фазовой скорости ограничений не существует.

22.5.Интерференция волн

Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связывают с понятием

когерентности. Волны называются когерентными, если разность их фаз остается постоянной во времени. Когерентными могут быть только волны,

228

имеющие одну частоту. При наложении когерентных волн наблюдается усиление или ослабление волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волны.

S1

r1

B

r2

S2

Рис.22.3

При наложении двух когерентных волн, (рис.22.3) возбужденных точечными источниками S1 и S2, колеблющимися с амплитудами А1 и А2 запишем волновые уравнения:

где r1 и r2 – расстояния от источников волн до рассматриваемой точки В, k-

волновое число; φ1 и φ2 –начальные фазы накладывающихся волн.

Амплитуда результирующей волны в точке В равна

Наблюдается интерференционный минимум, амплитуда результирующего колебания равна

A A1 A2 .

n– называется порядком интерференционного максимума или минимума

Геометрическое место точек в которых наблюдается усиление или ослабление результирующего колебания представляет собой семейство гипербол (рис.22.2), где между двумя интерференционными максимумами

(рис.22.2. сплошные линии) находятся интерференционные минимумы

(рис.22.2 штриховые линии).

22.6.Стоячие волны

Особым случаем интерференции являются стоячие волны они наблюдаются при наложении двух бегущих волн, распространяющихся навстречу друг другу. Запишем систему уравнений

При решении данной получается уравнение

подставим значение волнового числа, получим уравнение стоячей волны.

Стоячую волну можно изобразить, как показано на рис. 22.4.

Точки в которых амплитуда максимальна (Аст=2А) называются

пучностью. Точки в которых амплитуда равна нулю (Аст=0) называются узлами. Точки среды находящиеся в узлах колебаний не совершают.

230