21. Плотность распределения вероятностей непрерывной случайной величины и ее свойства.

Судить о хар-ре распр-ия в небольшой окрестности точек числ. оси позвол-т плотность распределения вер-ей. Рассм-м НСВ Х с интегр.непр-но диф-ой ф-ией распр-ия F(x).

Вер-ть попад-ия этой вел-ны в интервал (х,х+∆х) равна Р(х<X<x+∆x)=F(x+∆x)-F(x).

Вер-сть, к-рая находится на ед-цу длины рассмарт-го интервала: (Р(х<X<x+∆x))/∆x=(F(x+∆x)-F(x))/∆x.

Если мы перейдем к пределам, то получим вер-ть, кот. прих-ся на изолиров-ую точку Х: Пл-тью распр-ия вер-тей (диф.фун-ей распр-ия) наз-ся первая производная интегр. ф-ции распр-ния F(x):

f(x)=F’(x).

График ПР вер-тей – кривой распр-ия CВ Х.

Cв-ва ПР:

1.f(x)≥0 для люб.x – cв-во неотриц-ти.

3. -

Cв-во нормировки.

22.Математическое ожидание и дисперсия непрерывной случайной величины.

НСВ- св которая может принять любое значение из некоторого конечного или бесконечного интнрвала.

Геом.смысл: абсцесса центра тяжести криволин. трапеции огранич. графиком кр. распред-ия полигоном распред для ДСВ и Ох.

D(X)=M(X-M(X))²

σ (Х)= D(X)^1/2

D(X)= M(X)²-M²(X)

23.Равномерный закон распределения и его числовые характеристики.

Непр. случ. велич.х распред. равномерно на

отрезк [а;b], если её плотность вероятности

р(х) постоянна на этом отрезке и =0 вне его:

1/ (b-a), а< =х<=b

Р(х)= {

О, х<а, х>b

Функция распред. случайн. величины, расп-

ред-ой по равномерн. закону, имеет вид:

O, x<=a

F(x)= { (x-a)/(b-a), a<x<=b

1, x>b

График р(х) иF(х)на рис

Мат. ожидание и дисперсия равн. случ.

величины:

МХ=(а+b)/2; DХ=(b-а)( b-a)/ 12

24.Показательный закон распределения и его числовые характеристики.

Непрерывная СВ Х имеет показ. (экспоненциальное) распределение с параметром λ >0, если ее плотность распред-я имеет вид:

Ф-ция распределения СВ, распределенной по показ. з-ну:

Показательному распределению обычно подчиняется величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств, другими словами – величина промежутка времени между появлениями двух послед-х редких событий.

Вероятность попадания случайной величины Х на интервал (α;β)

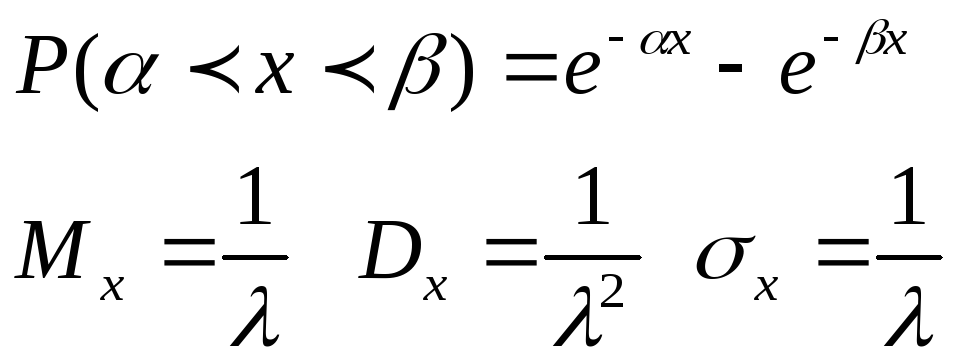
25.Нормальный закон распределения, его параметры и их вероятностный смысл. Зависимость формы нормальной кривой от параметров.

Влияние параметров а и σ на вид нормальной кривой.Нормальное распределение явл. одним из наиболее часто встречающихся. Играет большую роль в тер. вер., поскольку явл. Предельным законом, к к-ому приближаются все др. законы распределения.Док-но, что если знач. СВ возникают в результате большого числа независимых воздействий, ни одно из к-ых не превалирует над остальными, то результат этих воздействий явл. СВ, распределенной по нормальному закону почти всегда.По нормальному закону распределены:случайные ошибки измерения,лин. размеры деталей при массовом пр-ве,биометрические показатели лиц определенного возраста,отклонения в результате хим., спектральных и других анализах.

Говорят, что непрерывная СВ Х имеет нормальное распределение с параметрами а и σ, если ее плотность распределения имеет вид -(x- a)²/2σ²

f(x)=( 1/σ√2π) e

Определение корректно, т.к.:

_-∞∫^+∞f(x)dx=1

M(X)= _-∞∫^+∞xf(x)dx=a

σ (X)= _-∞∫^+∞(x-M(X))²f(x)=σ²

Для геометрической интерпретации параметров а и σ исследуют поведение ф-ии

-(x-a)²/2σ²

f(x)=( 1/σ√2π) e

график к-ой наз. нормальной кривой.

График симметр.относит.а

При изменении параметра а форма кривой не меняется, а ее график сдвигается влево или вправо. При изменении параметра σ меняется форма нормальной кривой: с увеличением параметра σ кривая должна приближаться к 0Х и растягиваться вдоль этой оси, а с уменьшением σ кривая стягивается к прямой х=а.

26.Вероятность попадания нормально распределенной случайной величины в заданный интервал; вероятность заданного отклонения. Чтобы найти вероятность попадания нормально распределенной случайной величины в заданный интервалс помощью функции Лапласа, сначала с.в. Х нормализуется (см. 4.24), а затем  используется следующая формула:

                                                      =

ормированное нормальное распределение имеет параметры и. Это распределение получается, еслипронормировать нормально распределенную величину X по формуле:                                                                    (4.24)

Плотность распределения вероятностей нормированного нормального распределения записывается в виде:     Вероятность заданного отклонения равна

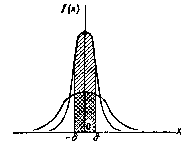
На рисунке наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-d,d),больше у той величины, которая имеет меньшее значение d. Этот факт полностью соответствует вероятностному смыслу параметра s .

27. Правило трех сигм и его значение для праклики При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D: Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа: Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее. На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.