ПИТАННЯ ДО ІСПИТУ (2-й СЕМЕСТР) 1. Означення функції декількох незалежних змінних. Геометричне зображення функції двох змінних.

Означення. Змінна величина z називається функцією двох незалежних змінних x та y , якщо кожній парі значень x; y із множини D ставиться у відповідність одне визначене значення z із множини E : z  fx; y. Означення. Множина D називається областю визначення функції z , а множина E  множиною її значень. Змінні x, y по відношенню до функції z називаються її аргументами. Означення. Областю визначення функції двох незалежних змінних z  fx; y називається множина пар значень x; y, при яких функція z визначена. Оскільки пара значень x; y визначає точку на площині xOy , то область D – частина площини xOy.

Для функції z  fx; y можна говорити про її графік. Якщо у просторі задана прямокутна декартова система координат і D – область визначення функції z  f(x, y) , то її графіком вважають множину M точок цього простору з координатами x; y; fx. Наприклад, графіком функції z  1  x  y, x  R, y  R є площина; графіком функції z  R 2  x 2  y 2 є верхня напівсфера.

Про графік функції трьох і більшого числа змінних у звичайному розумінні говорити неможливо. Такі функції можна вивчати за допомогою поверхонь рівня, а функції двох змінних – за допомогою ліній рівня. Означення. Лінією рівня функції z  f(x, y) називають множину точок площини xOy , в яких функція z набуває однакового значення. Отже, лінія рівня функції z  f(x, y) – лінія у площині xOy , яка задана рівнянням f(x, y)  c  const

2. Границя і неперервність функції 2-х змінних.

Означення. Дійсне число A називається границею функції z  fx; y в точці M0 x0 , y0  , якщо для будь-якої послідовності точок з області визначення функції M1 x1 , y1 , M2 x2 , y2 , , Mn xn , yn , що збігається до точки M0 x0 , y0  , відповідна послідовність значень функції fM1 , fM2 , , fMn  збігається до числа A . Означення. Функція z  fx; y називається неперервною в точці M0 (x0 , y0 ) , якщо границя функції в цій точці дорівнює значенню функції в цій точці:

(1)

Якщо позначити різниці ,

(2)

тобто неперервність функції z  fx; y у точці M0 (x0 , y0 ) означає, що нескінченно малим приростам x і y аргументів x і y відповідає нескінченно малий приріст функції f(x0 , y0 ) . Якщо рівність (1) не має місця, то функцію f(x, y) називають розривною в точці M0 (x0 , y0 ) . Множина точок розриву функції z  f(x, y) може утворювати лінію. Наприклад, функція розривна в кожній точці прямої y=x , оскільки вона не визначена в кожній точці цієї прямої 3. Частинні прирости та частинні похідні функції декількох незалежних змінних.

Нехай задані функція z  fx; y і точка x; y D . Якщо зміна функції z відбувається при зміні тільки одного з аргументів, наприклад x , при фіксованому значенні другого аргументу y, то функція набуває приросту _xz  f(x  x, y)  f(x, y) , який називається частинним приростом функції z по змінній x .

Означення. Частинною похідною функції z  fx; y по змінній x називається границя відношення частинного приросту функції по змінній x до приросту аргументу x , при умові, що приріст x прямує до нуля:

Аналогічно дається означення частинної похідної функції z=f(x, y) по змінній y:

При обчисленні частинних похідних користуються вже відомими правилами і формулами диференціювання функції однієї змінної, вважаючи при цьому другу змінну сталою.

Геометричний зміст похідної – похідна zx дорівнює тангенсу кута нахилу дотичної до кривої z  f(x, y0 ), y  y0 в точці M0 x0 ; y0  , тобто zx дорівнює тангенсу кута між дотичною і лінією, що проходить через точку M0 x0 ; y0  паралельно осі Ox

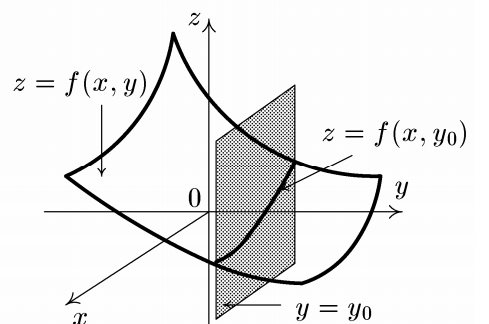
Аналогічно даються поняття частинних похiдних функцій трьох і більше змінних. Частинні похідні функції кількох змінних визначаються і обчислюються також в припущенні, що змінюється тільки одна з незалежних змінних, а інші при цьому фіксовані. Частинна похідна функції кількох змінних має той же механічний зміст, що і похідна функції однієї змінної – це швидкість зміни функції відносно зміни одного з аргументів. 4. Повний приріст. Повний диференціал функції 2-х незалежних змінних, застосування в наближених обчисленнях.

Означення. Повним приростом функції z  fx; y в точці x; y називається різниця z  f(x  y, y  y)  f(x, y), де x і y – довільні прирости аргументів. Означення. Функція z  fx; y називається диференційовною в точці M(x, y) , якщо її повний приріст f(x, y)  z  f(x  x, y  y)  f(x, y) можна подати у вигляді

Теорема (достатні умови диференційовності). Якщо функція z=f(x; y) має неперервні

частинні похідні в точці M(x, y) , то вона диференційовна в цій точці.

Означення. Повним диференціалом функції z=f(x; y) називається головна частина повного

приросту ∆z, лінійна відносно приростів аргументів ∆х і ∆у , тобто

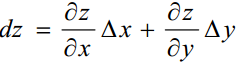
Диференціали незалежних змінних співпадають з їх приростами, тобто dx=∆x i dy=∆y .

Повний диференціал функції z=f(x, y) обчислюється за формулою:

Аналогічно, повний диференціал функції трьох змінних u=f(x; y; z) обчислюється за формулою:

Застосування диференціала у наближених обчисленнях Розглянемо функцію z  f(x; y) . Знайдемо повний приріст цієї функції:f(x, y)  f(x  x, y  y)  f(x, y) ,оскільки за формулою (3) f(x, y)  fx' (x, y)x  fy' (x, y)y , тоді f(x, y)  df(x, y) , яка в розгорнутому вигляді записується так: f(x  x, y  y)  f(x, y)  fx' (x, y)x  fy' (x, y)y . (4) Цією наближеною рівністю зручно користуватися, коли f(x, y), fx' (x, y) та fy' (x, y) легко обчислюються в точці M(x, y) . Наближена рівність (4) тим точніша, чим менші прирости x і y . 5. Частинні похідні вищих порядків.

Частинними похідними другого порядку функції z(x, y) називаються похідні від похідних 1 -го порядку.

Ф-ії двох змінних, від яких, у свою чергу, можна обчислювати частинні похідні. По відношенню до функції z(x, y) їх називають частинними похідними третього порядку:

У прикладі звертає на себе увагу рівність 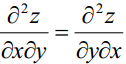, яка показує, що результат не залежить від порядку диференціювання. Частинні похідні називають мішаними. Виявляється, що (за умови їх неперервності) вони рівні, тобто результат не залежить від порядку диференціювання: (5) У випадку розривності мішаних частинних похідних рівності (5) можуть і не мати місця 6. Похідна за напрямком. Градієнт функції декількох змінних.

Нехай функція z  fx; y визначена в деякому околі точки M0 x0 , y0  , l - вектор з початком в точці M0 x0 , y0  , Mx, y - довільна точка, що належить вектору l , l - довжина відрізка M0M

Якщо існує , то ця границя називається похідною функціїz  fx; y у напрямку l і позначається:

Зокрема, частина похідна дz/дx є похідна функціїz fx;yу додатному напряму осіOx , а дz/дy похідна у додатному напряму осіOy . Розглянемо одиничний векторlcos; cosабоlcos; sin, де,- кути, що утворює векторl з додатними напрямами осейOx іOy :

Теорема. Якщо функціяz fx;yмає в точціM0x0 ,y0неперервні частинні похідні першого порядку дz/дxідz/ду, то в цій точці існує похідна у будь-якому напрямуlcos; sin, причому

, де дz/дx і дz/ду - значення частинних похідних в точці M0 x0, y0).

Економічний зміст – похідна у напрямку від виробничоїтфункції є кількість продукції, що припадає на одиницю лінійної комбінації факторів. Розглянемо вектор . Знайдемо скалярний добуток векторівa і l :

, звідки набуває найбільшого значення при cos  1,   0 . Отже, найбільше значення.

Означення. Градієнтом функції z  fx; y називається вектор площини xOy , який має координати:

Напрям grad z є напрямом найбільшої зміни функції z  fx; y, модуль градієнта дорівнює найбільшому значенню похідної функції z  fx; y в даній точці у будь-якому напрямку:

У випадку функцiї трьох незалежних змінних u  fx; y; z :