
Демо вариант
.doc
|
Геометрическая комбинация «цилиндр — призма» |
|
|
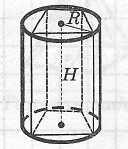
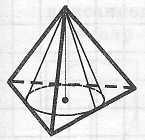
Свойства цилиндра, описанного около призмы
|
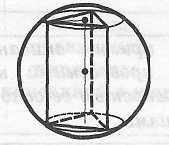
Цилиндр
можно описать около прямой призмы,
если ее основание - многоугольник,
около которого можно описать окружность.
При этом радиус
цилиндра
Ось
цилиндра лежит на одной прямой с
высотой
|
|
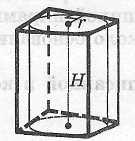
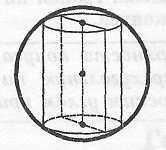
Свойства цилиндра, вписанного в призму
|
Цилиндр
можно вписать в прямую призму, если
ее
основание - многоугольник, в который
можно вписать
окружность. При этом радиус цилиндра
Ось
цилиндра лежит на одной прямой с
высотой
|
|
Геометрическая комбинация «конус-пирамида» |
|
|
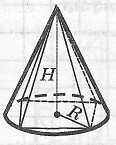
Определение конуса, описанного около пирамиды
|
Конус называется описанным около пирамиды, если его вершина совпадает с вершиной пирамиды, а основание конуса описано около основания пирамиды. При этом пирамида называется вписанной в конус. |
|
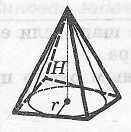
Свойства конуса, описанного около пирамиды
|
Конус можно описать около пирамиды, если ее основание - многоугольник, около которого можно описать окружность, а высота пирамиды проходит через центр этой окружности.
Радиус
|
|
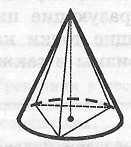
Определение конуса, вписанного в пирамиду
|
Конус называется вписанным в пирамиду, если его вершина совпадает с вершиной пирамиды, а основание конуса вписано в основание пирамиды. При этом пирамида называется описанной около конуса. |
|
Свойства конуса, вписанного
|
Конус
можно вписать в пирамиду, если ее
основание
- многоугольник, в который можно вписать
окружность, а высота пирамиды проходит
через
центр этой окружности.
Радиус
|
|
Геометрическая комбинация «шар — цилиндр» |
|
|
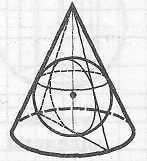
Определение цилиндра, вписанного в шар
|
Цилиндр называется вписанным в шар, если его основания являются сечениями шара. При этом шар называется описанным около цилиндра. |
|
Свойства цилиндра, вписанного в шар
|
Шар можно описать около любого прямого кругового цилиндра. Центр шара лежит на середине высоты цилиндра, соединяющей центры его оснований. Осевое сечение цилиндра является прямоугольником, вписанным в большой круг шара.
Радиус
шара
|
|
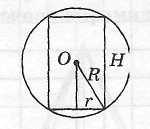
Определение цилиндра, описанного около шара
|
Цилиндр называется описанным около шара, если шар касается оснований цилиндра в их центрах и боковой поверхности цилиндра по окружности большого круга шара, параллельной основаниям цилиндра. При этом шар называется вписанным в цилиндр. |
|
Свойства цилиндра, вписанного в шар
|
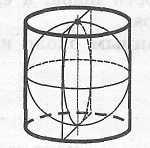
Шар можно вписать только в равносторонний цилиндр (т. е. в цилиндр, в котором высота равна диаметру основания). Центр шара лежит на середине высоты цилиндра, соединяющей центры его оснований.
Осевое
сечение цилиндра является квадратом,
в который
вписан большой круг шара. Радиус
шара
|
|
|
|
|
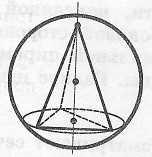
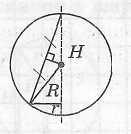
Определение конуса, вписанного в шар
|
Конус называется вписанным в шар, если вершина конуса лежит на поверхности шара, а его основание является сечением шара. При этом шар называется описанным около конуса.
|
|
Свойства конуса, вписанного в шар
|
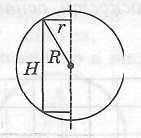
Шар можно описать около любого конуса. Центр шара лежит на оси конуса и является центром окружности, описанной около осевого сечения конуса.
Радиус
шара
|
|
Замечание.
В
некоторых задачах, связанных с конусом,
вписанным в шар, необходимо рассматривать
два случая:
|
|
|
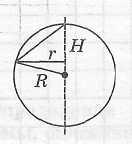
Определение конуса, описанного около шара
|
Конус называется описанным около шара, если шар касается основания конуса в его центре и боковой поверхности конуса по окружности, параллельной основанию конуса. При этом шар называется вписанным в конус.
|
|
Свойства конуса, описанного около шара
|
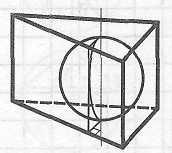
Шар можно вписать в любой конус. Центр шара лежит на оси конуса и является центром окружности, вписанной в осевое сечение конуса.
Радиус
шара
|
|
Геометрическая комбинация «шар — призма» |
|
|
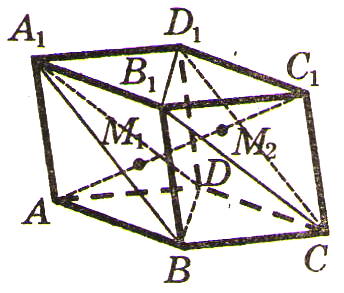
Определение призмы, вписанной в шар
|
Призма называется вписанной в шар, если все ее вершины лежат на поверхности шара. При этом шар называется описанным около призмы. |
|
Свойства призмы, вписанной в шар
|
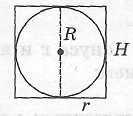
Шар можно описать около прямой призмы, если около ее оснований можно описать окружности. Центр шара лежит на середине высоты призмы, соединяющей центры этих окружностей. При решении задач обычно рассматривают сечение полуплоскостью, проходящей через центр шара и боковое ребро призмы.
Радиус
шара
|
|
Определение призмы, описанной около шара
|
Призма называется описанной около шара, если все ее грани касаются поверхности шара. При этом шар называется вписанным в призму. |
|
Свойства призмы, описанной около шара
|
Шар можно вписать в прямую призму, если в ее основания можно вписать окружности, а высота призмы равна диаметрам этих окружностей. Центр шара лежит на середине высоты призмы, соединяющей центры этих окружностей. При решении задач обычно рассматривают сечение полуплоскостью, проходящей через центр шара и перпендикулярной к боковой грани призмы.
Радиус
шара
|
|
Геометрическая комбинация «шар — пирамида» |
|
|
Определение пирамиды, вписанной в шар
|
Пирамида называется вписанной в шар, если все ее вершины лежат на поверхности шара. При этом шар называется писанным около пирамиды.
|
|
Свойства правильной пирамиды, вписанной в шар
|
Шар можно описать около любой правильной пирамиды. Центр шара лежит на прямой, содержащей высоту пирамиды, и совпадает с центром окружности, описанной около равнобедренного треугольника, боковой стороной которого является боковое ребро пирамиды, а высотой - высота пирамиды. Радиус шара равен радиусу этой окружности. |
|
При решении задач обычно рассматривают сечение полуплоскостью, проходящей через центр шара и боковое ребро пирамиды.
Радиус
шара
|
|
|
Замечание.
В
некоторых задачах, связанных с
пирамидой,
вписанной в шар, необходимо рассматривать
два случая:
|
|
|
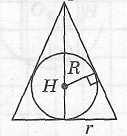
Определение пирамиды, описанной около шара
|
Пирамида называется описанной около шара, если все ее грани касаются поверхности шара. При этом шар называется вписанным в пирамиду. |
|
Свойства правильной пирамиды, описанной около шара
|
Шар можно вписать в любую правильную пирамиду. Центр шара лежит на высоте пирамиды и совпадает с центром окружности, вписанной в равнобедренный треугольник, боковой стороной которого является апофема правильной пирамиды, а высотой - высота пирамиды. Радиус шара равен радиусу этой окружности. При решении задач обычно рассматривают сечение полуплоскостью, проходящей через центр шара и апофему пирамиды.
Радиус
шара
|
|
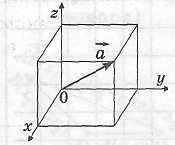
ВЕКТОРЫ В ПРОСТРАНСТВЕ |
|||||||
|
1. Понятие вектора в пространстве |
|||||||
|
Определение вектора
|
Вектором называется отрезок, для которого указано, какой из его концов считается началом, а какой концом. Вектор, начало и конец, которого совпадают, называется нулевым. Все обозначения для векторов в пространстве совпадают с аналогичными обозначениями на плоскости. |
||||||
|
Определение длины вектора |
Длиной (абсолютной величиной, модулем) ненулевого вектора называется длина отрезка, изображающего вектор. Длина нулевого вектора считается равным нулю. |
||||||
|
Определение коллинеарных сонаправленных и противоположно направленных векторов
|
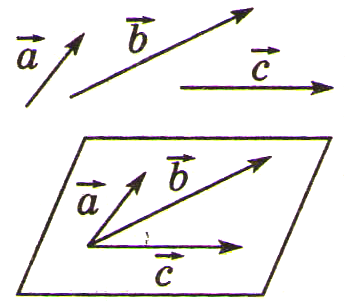
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Векторы
Векторы
|
||||||
|
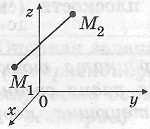
Полезная задача |
Докажите,
что точки
|
||||||
|
Определение равных векторов
|
Векторы
называются равными,
если они сонаправлены и их длины равны:
|
||||||
|
Опорная задача (о векторе равном данному)
|
От любой точки можно отложить вектор, равный данному, и притом только один.
|
||||||
|
2. Действия с векторами |
|||||||
|
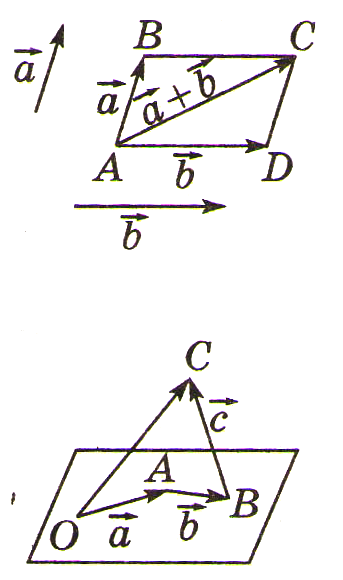
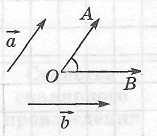
Правила сложения векторов
для коллинеарных векторов
|
1. Правило
треугольника:
Для любых трех
точек
2.
Правило
параллелограмма (для двух неколлинеарных
векторов):
3. Правило
многоугольника (для нескольких
векторов):
Если
|
||||||
|
Свойства сложения векторов |
Для
любых векторов
1)
2)
3)
|
||||||
|
Определение противоположных векторов
|
Два ненулевых вектора называются противоположными, если они противоположно направлены и их длины равны.
|
||||||
|
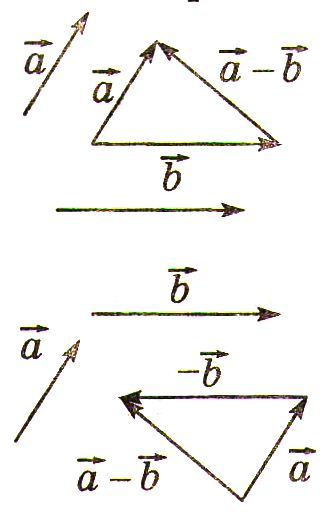
Определение разности векторов |
Разностью
векторов
|
||||||
|
Правила вычитания векторов
|
1. Правило треугольника: Если уменьшаемое и вычитаемое – векторы с общим началом, то вектор разности стягивает их концы и направлен от конца вычитаемого к концу уменьшаемого. 2.Сложение
уменьшаемого с вектором, противоположным
вычитаемому:
|
||||||
|
Опорная задача (условие коллинеарности двух векторов) |
Если
векторы
|
||||||
|
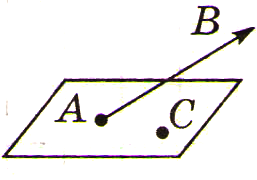
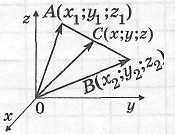
3. Компланарные векторы |
|||||||
|
Определение компланарных векторов
|
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
|
||||||
|
Замечание. Понятие компланарности является пространственным аналогом понятия коллинеарности. |
|||||||
|
Свойства компланарных векторов |
1. Любые два вектора компланарны. 2. Любые три вектора, из которых два являются коллинеарными, компланарны. 3. Любые три вектора, из которых хотя бы один – нулевой, компланарны. 4. Если векторы компланарны, то существует плоскость, параллельная каждой из прямых, содержащих эти векторы. |
||||||
|
Опорная задача (критерий компланарновти трех векторов) |
Если вектор
И
обратно: если векторы
|
||||||
|
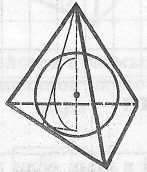
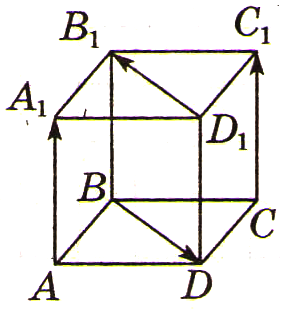
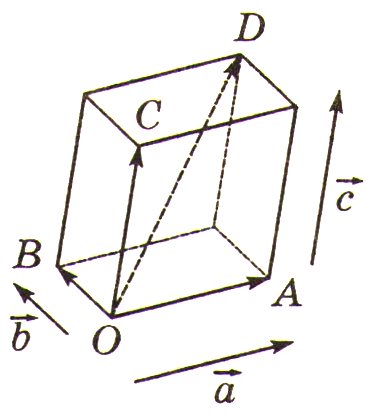
Правило параллелепипеда (для сложения трех некомпланарных векторов)
|
Вектором – суммой
трех некомпланарных векторов является
направленная диагональ параллелепипеда,
построенного на трех данных векторах
как на ребрах:
|
||||||
|
Замечание. Правило параллелепипеда является пространственным аналогом правила параллелограмма для сложения двух векторов на плоскости. |
|||||||
|
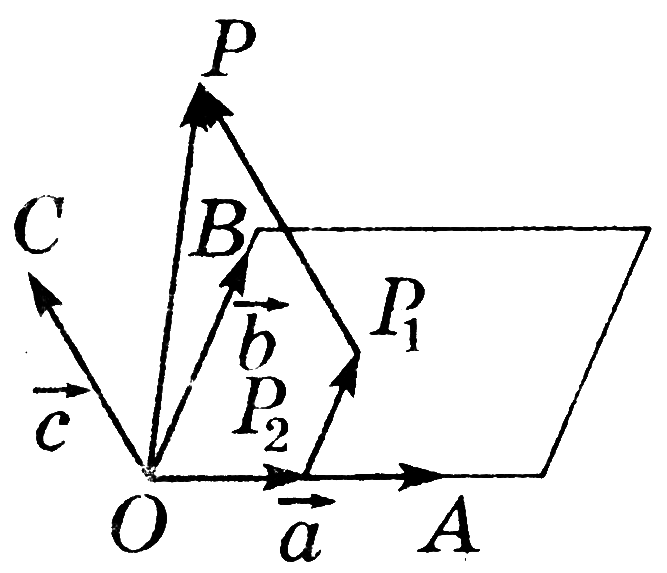
Определение разложения вектора |
Если вектор
где
|
||||||
|
Замечание.
Говорят
также, что вектор
|
|||||||
|
Теорема (о разложении вектора по трем некомпланарным векторам)
|
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
|
||||||
|
Замечание.
Любые три
некомпланарных вектора
|
|||||||
|
Опорная задача (формула Эйлера для точки пересечения медиан треугольника)
|
Если
|
||||||
|
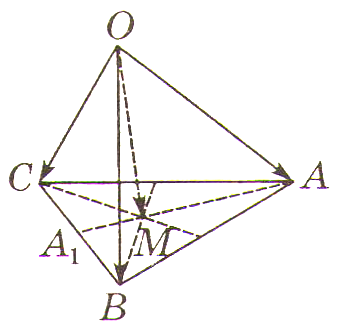
Опорная задача (о делении диагонали параллелепипеда на три равные части)
|
Диагональ
|
||||||
|
МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ |
|||||||
|
1. Координаты точки и координаты вектора |
|||||||
|
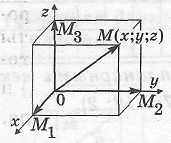
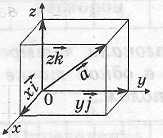
Определение прямоугольной системы координат в пространстве
|
Прямоугольная система координат в пространстве образована тремя попарно перпендикулярными прямыми (осями координат), на каждой из которых выбрано направление и единица измерения отрезков, проходящими через одну точку пространства (начало координат).
Плоскости
Начало координат разделяет каждую из осей на два луча - положительную полуось (ее направление совпадает с направлением оси) и отрицательную полуось (ее направление противоположно направлению оси). |
||||||
|
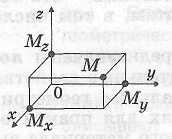
Определение координат точки
|
Обозначение.
Координаты
точки указывают после
ее обозначения в круглых скобках в
таком порядке:
абсцисса
- ордината - аппликата,
т. е.
|
||||||
|
Расположение точки
|
Плоскость
|
Плоскость
|
Плоскость
|
Ось
|
Ось
|
Ось
|
|
|
Координаты точки |
|
|
|
|
|
|
|
|
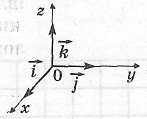
Определение координатных векторов
|
Координатными векторами (ортами) называются единичные (т. е. с длиной, равной единице) векторы, отложенные от начала координат на каждой из положительных полуосей.
|
||||||
|
Определение координат вектора
|
Так
как координатные векторы некомпланарны,
то
любой вектор
Координатами
вектора
Обозначение.
Координаты
вектора указывают после
его обозначения в фигурных скобках в
таком
порядке:
|
||||||
|
Свойства координат векторов
|
1.
Нулевой вектор имеет координаты
2. Координаты равных векторов равны, и обратно: если координаты двух векторов равны, то эти векторы равны. |
||||||
|
Действия с векторами в координатах
|
1. Каждая координата суммы двух или нескольких векторов равна сумме соответствующих координат этих векторов. 2. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. 3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. |
||||||
|
Опорная задача (необходимое и достаточное условие коллинеарности двух векторов) |
Координаты двух коллинеарных векторов
пропорциональны,
и обратно: если
координаты двух
векторов пропорциональны, то эти
векторы
коллинеарны,
то есть векторы
|
||||||
|
Замечание.
Если
координата одного из коллинеарных
векторов равна нулю, то соответствующая
координата
другого вектора также равна нулю, то
есть
|
|||||||
|
Определение радиус-вектора
|
Радиус-вектором
данной
точки называется вектор,
конец которого совпадает с этой точкой,
а начало
—
с
началом
координат,
|
||||||
|
Опорная
задача
(о
равенстве координат
точки
и
ее радиус-вектора.
|
Координаты любой точки равны соответствующим координатам ее радиус - вектора.
|
||||||
|
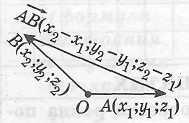
Опорная задача (о вычислении координат вектора)
|
Каждая координата вектора равна разности соответствующих координат его конца и начала.
|
||||||
|
2. Простейшие задачи в координатах |
|||||||
|
Опорная задача (формулы координат середины отрезка)
|
Каждая
координата середины отрезка равна
полусумме
соответствующих координат его концов:
|
||||||
|
Опорная задача (формула длины вектора)
|
Длина
вектора
|
||||||
|
Опорная задача (формула расстояния между двумя точками)
|
Расстояние
между точками
|
||||||
|
Замечание.
В
отличие
от аналогичной задачи на плоскости
в пространстве равенств
|
|||||||
|
3. Скалярное произведение векторов |
|||||||
|
Определение угла между векторами
|
Углом
между не сонаправленными векторами
Если
векторы
Обозначение.
Угол
между векторами
|
||||||
|
Определение перпендикулярных векторов |
Векторы
Обозначение.
|
||||||
|
Определение скалярного произведения векторов
|
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними:
Обозначение.
Скалярное
произведение векторов
|
||||||
|
Замечание. Скалярное произведение векторов является не вектором, а числом. |
|||||||
|
Определение скалярного квадрата |
Скалярным
квадратом
вектора
|
||||||
|
Замечание.
Очевидно,
что скалярный квадрат вектора
равен квадрату его длины: |
|||||||
|
Опорная задача (о перпендикулярности двух векторов) |
Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. |
||||||
|
|
Скалярное
произведение векторов
|
||||||
|
Следствие
|
Косинус
угла
|
||||||
|
Свойства скалярного произведения
|
Для
любых векторов
|
||||||
|
Опорная задача (о представлении координат вектора) |
Координаты
ненулевого вектора
|
||||||
|
|
Ненулевой вектор называется направляющим вектором прямой, если он лежит либо на данной прямой, либо на прямой, параллельной данной. |
||||||
|
Замечание.
Координаты
направляющего вектора
легко определить, зная координаты
двух точек
данной прямой: если
|
|||||||
|
Полезная задача
|
Докажите,
что уравнение прямой, проходящей через
точку
|
||||||
|
Опорная задача (о вычислении угла между прямыми в пространстве) 1)
2)
|
Угол
|
||||||
|
прямой и плоскостью)
|
Угол
где
|
||||||
|
Замечание.
Ненулевой
вектор
|
|||||||

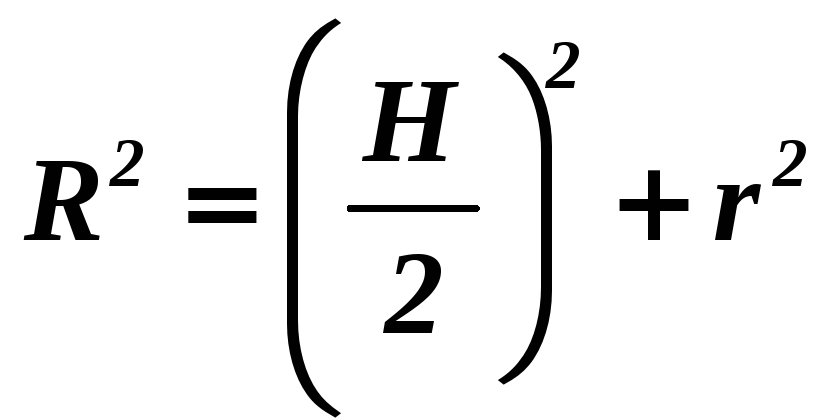 .
.
 Геометрическая
комбинация «шар
— конус»
Геометрическая
комбинация «шар
— конус»
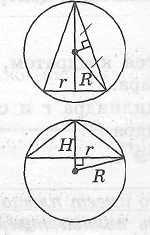
 .
.
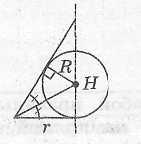
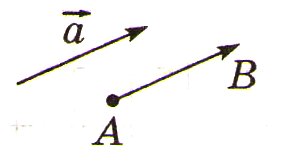

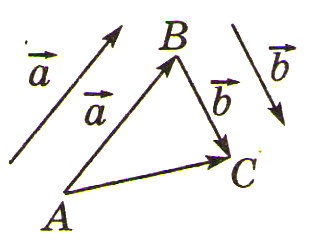

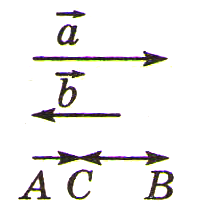


 Опорная
задача (о
вычислении скалярного
произведения
векторов
с заданными координатами)
Опорная
задача (о
вычислении скалярного
произведения
векторов
с заданными координатами)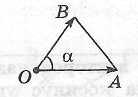
 .
. Определение
направляющего
вектора
прямой
Определение
направляющего
вектора
прямой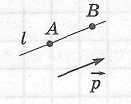
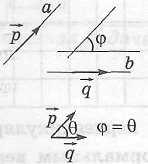
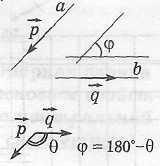
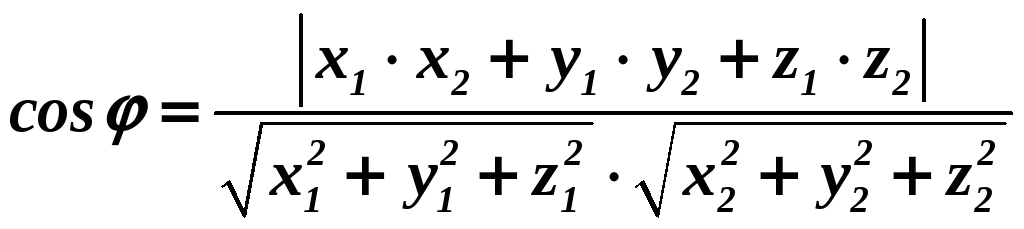 .
. Опорная
задача
(о
вычислении
угла
между
Опорная
задача
(о
вычислении
угла
между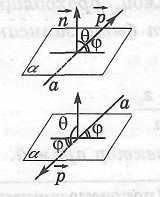
 ,
,