
Представления знаний в информационных системах
.pdfГлава 4 ПРИМЕНЕНИЕ НЕЧЕТКОЙ ЛОГИКИ
ВЭКСПЕРТНЫХ СИСТЕМАХ
4.1.Предпосылки возникновения нечеткой логики
Зачастую поиск оптимального решения практической задачи на основе классических методов математики затруднен. Причина заключа- ется в проблеме осуществления корректного подбора приемлемого ана- литического описания решаемой задачи. Даже в случае успешной реа-
лизации аналитического описания поставленной задачи для ее решения могут потребоваться непомерные временные и материальные затраты. Однако существует другой подход к решению проблемы.
Дело в том, что человек способен находить оптимальные реше- ния, пользуясь лишь абстрактными сведениями и субъективными пред- ставлениями о задаче. В жизни нам постоянно приходится оперировать неточными знаниями и формально не определенными понятиями. Ра- зумеется, что классическая математика в таких условиях не применима. Указанные обстоятельства и привели к возникновению новой математи- ческой дисциплины – нечеткой логики, позволяющей приблизить мате- матику к реальному миру.
Нечеткая логика (fuzzy logic) является надмножеством классиче- ской булевой логики. Она расширяет возможности классической логи- ки, позволяя применять концепцию неопределенности в логических вы- водах. Под термином “нечеткая логика” фактически понимается непре- рывная логика, поскольку в данном случае вместе со значениями “ложь” и “истина” применяются значения между ними [1, 2].
Как новая область математики, нечеткая логика была представле- на в 1960-х годах профессором Калифорнийского университета Лотфи Заде (Lotfi Zadeh). Первоначально нечеткая логика разрабатывалась как средство моделирования неопределенности человеческого языка.
Его основная идея состояла в том, что человеческий способ рас- суждений, опирающийся на естественный язык, не может быть описан в рамках традиционных математических понятий. Этим понятиям при- суща строгая однозначность интерпретации, а все, что связано с ис- пользованием естественного языка, имеет многозначную интерпре-
тацию [3, 9, 13–16].
81
Лотфи Заде ввел понятие лингвистической переменной [1]. Лин-
гвистическая переменная – это переменная, значения которой опреде- ляются набором вербальных (то есть словесных) характеристик неко-
торого свойства. Например, лингвистическая переменная “возраст” оп-
ределяется через набор: младенческий, детский, юношеский, молодой, зрелый, преклонный и старый.
Таким образом, основной целью введения нечеткой логики явля- ется создание аппарата, способного моделировать человеческие рассуж- дения и объяснять человеческие приемы принятия решений в ходе ре- шения различных задач. В настоящее время нечеткая логика применя- ется при разработке систем, понимающих тексты на естественном язы- ке, при создании планирующих систем, опирающихся на неполную ин- формацию, для обработки зрительных сигналов, при управлении техни- ческими, социальными и экономическими системами, в системах искус- ственного интеллекта и робототехнических системах.
4.2. Нечеткая логика
Одно из базовых понятий в нечеткой логике это теория нечетких множеств. Эта теория занимается рассмотрением множеств, определяе- мых небинарными отношениями вхождения. В булевой логике суще- ствует только два варианта: либо элемент принадлежит множеству (степень вхождения равна 1), либо не принадлежит ему (степень вхож- дения равна 0). В нечеткой логике принимается во внимание степень вхождения во множество данного элемента, которая может непрерывно изменяться в интервале от 0 до 1. Указанной степени вхождения эле-
мента во множество соответствует понятие функции принадлежности элемента множеству.
Для комбинирования нецелочисленных значений истинности в
нечеткой |
логике |
определяются |
эквиваленты операций |
И, ИЛИ, НЕТ [3, 14]: |
|
|
|
|
p1Иp2 = min( p1, p2 ) |
(т.е. меньшее); |
|
p1ИЛИp2 = max(p1, p2 ) (т.е. большее); НЕp1 = 1− p1 (т.е. обратное значение).
Существенной в нечеткой логике является проблема взвешивания сведений. Предположим, что имеется следующий набор продукционных правил:
82
Правило 1:
ЕСЛИ x программирует на ЭВМ
И x получает новую информацию через Интернет, ТО x выберет специальность по информатике.
Правило 2:
ЕСЛИ x не склонен к изучению гуманитарных наук И x не любит доказывать теоремы,
ТО x выберет специальность по информатике.
Предположим, что мы видели, как x программировал задачу на компьютере (определенность равна 1), и вполне уверены (0,8), что x получает новую информацию через Интернет. Тогда условия, входящие в правило 1, имеют совместное значение степени истинности, равное 0.8, поскольку в случае логической функции И мы используем опера- цию min.
Для правила 2 мы знаем, что “ x не склонен к изучению гумани- тарных наук” (0.5) и “ x не любит доказывать теоремы” (степень истин- ности 0.25), тогда степень истинности заключения “ x выберет специ- альность по информатике” равна 0.25 (меньшему из значений).
Таким образом, возникает проблема определения результирую-
щей степени истинности заключения на основании приведенных двух правил. Следует отметить, что исследование таких проблем относится в большей степени к теории свидетельств, чем к нечеткой логике.
Схема, использующая свидетельства, для получения степени уве- ренности была предложена Шортлиффом и применяется в ЭС MYCIN. Она основывается на коэффициентах уверенности, предназначенных для измерения степени доверия к заключению, которое является резуль- татом полученных свидетельств. Коэффициент уверенности – это раз- ность между двумя мерами:
КУ[h : e] = МД[h : e] − МНД[h : e],
где КУ[h : e] – уверенность в гипотезе h с учетом свидетельства e; МД[h : e] – мера доверия гипотезе h при заданном свидетельстве e; МНД[h : e] – мера недоверия h при свидетельстве e.
Коэффициент КУ может изменяться от –1 (абсолютная ложь) до 1 (абсолютная истина). Значения МД и МНД могут изменяться толь-
83
ко от 0 до 1. Следует отметить, что КУ , МД и МНД не являются ве- роятностными мерами.
Шортлиффом была предложена формула уточнения, по которой новую информацию можно сочетать со старыми результатами. Она применяется к мерам доверия и недоверия, связанным с каждой гипоте- зой. Формула для меры доверия имеет следующий вид:
МД[h : e1,e2 ] = МД[h : e1] + МД[h : e2 ](1− МД[h : e1]),
где запятая между e1 и e2 означает, что e2 следует за e1. Аналогичным
образом уточняются значения меры недоверия.
Смысл формулы состоит в том, что влияние второго свидетельст- ва e2 на гипотезу h при заданном свидетельстве e1 сказывается в сме-
щении меры доверия в сторону полной определенности на расстояние, зависящее от второго свидетельства. Эта формула имеет два важных свойства:
а) она симметрична относительно следования e1 и e2 ;
б) по мере накопления подкрепляющих свидетельств МД (или МНД ) движется в сторону полной определенности.
Рассмотрим пример, указывая в скобках значение МД для свиде- тельств.
Правило 1:
ЕСЛИ x программирует на ЭВМ (0.75)
И x не любит теоретические дисциплины (0.6), ТО x выберет специальность по информатике. Правило 2:
ЕСЛИ x любит увлекаться точными науками (0.5) ИЛИ x любит практику на ЭВМ (0.7),
ТО x выберет специальность по информатике.
Операция И в первом правиле определяет минимальное из зна- чений 0.75 и 0.6 , т.е. 0.6. Операция ИЛИ во втором правиле требует взятия максимального из значений 0.5 и 0.7, т.е. 0.7.
Тогда гипотеза, что “ x выбирает специальность по информатике” поддерживается на уровне 0.6 правилом 1 и на уровне 0.7 правилом 2. Применяя приведенную формулу, получаем
84
МД [информатика: правило 1, правило 2] =
= МД [информатика: правило 1] + МД [информатика: правило 2]×
×(1 − МД [информатика: правило 1]) = 0,88.
Таким образом, объединенная мера доверия оказывается выше, чем при учете каждого свидетельства, взятого отдельно. Это согласует- ся с ожидаемым нами результатом, поскольку несколько показывающих одно и то же направление свидетельств подкрепляют друг друга. Сле- дует отметить, что если поменять порядок правил 1 и 2, то на результате это не отразится. Такой набор правил с успехом использовался в ЭС MYCIN, что привело к их широкому применению в последующих раз- работках.
Отношение правдоподобия гипотез. Представляет интерес оста-
новиться на применении теоремы Байеса для связывания информации, поступающей из различных источников [14]. Этот подход позволяет вычислить относительное правдоподобие конкурирующих гипотез ис- ходя из силы свидетельств. В основе применяемого правила лежит фор-
мула
ОП(H : E) = P(E : H ) / P(E : H '),
где отношение правдоподобия (ОП ) определяется как вероятность со- бытия или свидетельства E , при условии заданной конкретной гипоте- зы H , деленная на вероятность этого свидетельства при условии лож-
ности данной гипотезы ( H '). Таким образом, если мы знаем вероятно- сти свидетельства при заданной гипотезе и ее дополнение, то мы можем
определить правдоподобие данной гипотезы на основе имеющегося свидетельства.
Например, если мы знаем вероятность появления отличных оце- нок на вступительном экзамене среди абитуриентов-медалистов и веро- ятность появления отличных оценок среди остальных абитуриентов, то мы сможем вычислить вероятность того, что абитуриент, сдавший всту- пительный экзамен на “отлично”, является медалистом.
Отношение правдоподобия может быть использовано для уточне- ния шансов в пользу рассматриваемой гипотезы, если становится из- вестно, что произошло событие E . Следуя [3, 14], приведем правило Байеса, используя понятие шансов. Шансы O(A) за
наличии некоторого события X можно записать в виде
O(A) = P(A / X ) / P(B / X ) = P(A / X ) /[1− P(A / X )].
85
Полагая O = O(A) и P = P(A / X ), получаем выражения для со- отношений между величинами O и P:
O = P /(1− P); P = O /(1+ O).
Байесовская схема уточнения сводится к выражению [14]
O'(H ) = O(H )× ОП(H : E),
где O(H ) – априорные шансы в пользу H , а O'(H ) – результирую-
щие апостериорные шансы, при условии наступления события E , в со- ответствии с соотношением правдоподобия.
При этом информация от различных источников может учиты- ваться простым умножением. В случае заданных априорных шансов для конкурирующих гипотез и событий, про которые известно, что они произошли, легко вычисляются апостериорные шансы, а вслед за ними и вероятности. Отношения правдоподобия получаются из двумерной таблицы, показывающей, насколько часто случается каждое событие при каждой из гипотез.
В качестве примера в табл. 4.1 содержатся данные о продолжи- тельности жизни 100 человек. Из них 44 человека прожили более 75 лет, а остальные – 75 лет и меньше, причем указано, кто среди них был ку- рильщиком, а кто – нет.
Таблица 4.1
Отношение к |
Продолжительность |
Продолжительность |
Всего |
курению |
жизни > 75 лет |
жизни ≤ 75 лет |
|
Курящие (чел.) |
20 |
33 |
53 |
Некурящие (чел.) |
24 |
23 |
47 |
Всего |
44 |
56 |
100 |
Априорные шансы в этой выборке из 100 случаев в пользу того, что человек проживет более 75 лет:
O( Долгожитель) = 44/ 56 =11/14 = 0,7857,
а отношения правдоподобия
OП( Долгожитель : Курящий) = (20 / 44) /(33/ 56) = 0,8815;
OП( Долгожитель: Некурящий) = (24/ 44) /(23/ 56) =1,3280.
Предположим, что пол также принимается во внимание, как еще одна переменная, имеющая отношение к долгожительству (табл. 4.2).
86
Таблица 4.2
Пол |
Продолжительность |
Продолжительность |
Всего |
|
жизни > 75 лет |
жизни ≤ 75 лет |
|
Мужчины (чел.) |
20 |
36 |
56 |
Женщины (чел.) |
24 |
20 |
44 |
Всего |
44 |
56 |
100 |
Из табл. 4.2 следуют выражения для соотношений правдоподобия
для мужчин
OП( Долгожитель: Мужчина) = (20/ 44) /(36/ 56) = 0,7071
и для женщин
OП( Долгожитель : Женщина) = (24 / 44) /(20 / 56) =1,5273.
Теперь, учитывая, что априорные шансы в пользу продолжитель- ной жизни (свыше 75 лет) равны 11/14 = 0,7857, мы можем вычислить апостериорные шансы того, что курящий мужчина проживет долгую жизнь, пользуясь выражением
O′( Долгожитель) = OП( Долгожитель: Курящий)×
´OП( Долгожитель: Мужчина)´O( Долгожитель) =
=0,8815×0,7071×0,7857 = 0,4897.
Это значение соответствует вероятности 0,3288, тогда как началь- ная вероятность была 0,44. Таким оказался результат учета двух нега- тивных факторов.
Отношения правдоподобия всегда положительны, причем ОП >1 указывает на свидетельства в пользу гипотезы, ОП <1 – против нее, а ОП =1 говорит о том, что свидетельства не влияют на правдоподобие рассматриваемой гипотезы.
Множитель ОП показывает, насколько более вероятной стано- вится данная гипотеза при наличии свидетельств, чем при их отсутст- вии.
Если свидетельства сами по себе вызывают сомнения, то целесо- образно построить масштабированное ОП′ , такое, что
ОП′ = ОП × ВС + (1- ВС),
где ВС – вероятность того, что свидетельство надежно. Например, если свидетельство известно с вероятностью p = 0,8, то отношение правдо-
подобия, равное 1,2 (в пользу гипотезы), согласно приведенному соот- ношению уменьшится до 1,16.
87
Таким образом, можно сделать вывод, что отношения правдопо- добия дают следующие преимущества:
∙допускают комбинирование нескольких источников данных;
∙возможна их корректировка, если свидетельство ненадежно.
4.3. Нечеткие подмножества
Пусть E есть множество, A – подмножество E, т.е. А E. Принад- лежность любого элемента x подмножеству A можно выразить с помо- щью функции принадлежности μA (x) , значения которой указывают, яв-
ляется ли (да или нет) x элементом A: |
|
|
|
μ A (x) = 1, |
если |
x A, |
|
μ A (x) = 0, |
если |
x A. |
|
Предположим теперь, что характеристическая функция для эле- |
|||
ментов подмножества A может принимать не только значения 0 |
или |
||
1, но и любое значение а [0,1], т.е. μ A (x) = a [0,1]. |
A = |
||
Математический объект, |
определяемый выражением |
||
= {(x1 | 0,2),(x2 | 0,4),(x3 |1),(x4 | 0)}, где |
xi – элемент универсального |
||
множества E, а число после вертикальной черты – значение функции принадлежности для этого элемента, будем называть нечетким подмно- жеством множества E.
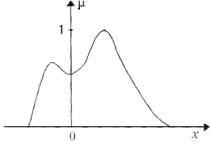
На рис. 4.1 приведено графическое представление нечеткого мно- жества с помощью его функции принадлежности [3].
Рис. 4.1. Функция принадлежности
Строгое определение понятия нечеткого подмножества имеет сле- дующий вид. Пусть E есть множество и x – элемент E. Тогда нечетким подмножеством A множества E называется множество упорядоченных
пар
{x | μ A(x)}, x E ,
88
где μA (x) – степень принадлежности x к A. Если μ A (x) принимает свои
значения во множестве M значений функции принадлежности, то можно сказать, что x принимает значения в M посредством μA . Множество M
называют множеством принадлежностей.
Операции над нечеткими множествами. Рассмотрим различные операции теории обычных множеств применительно к нечетким под- множествам, а также введем новые операции для нечетких подмножеств. Пусть Е – множество и М=[0,1] – множество принадлежностей, А и B – два нечетких подмножества из Е.
Равенство. Два нечетких подмножества A и B равны (обозначает- ся A=B) тогда и только тогда, когда
(A = B) Û ("x Î E : μ A (x) = μB (x)) .
Если найдется, по крайней мере, один такой элемент x из E, что равенство μA (x) = μB (x) не удовлетворяется, то A и B не равны
( A ¹ B ).
Пересечение. Пересечение двух нечетких подмножеств A и B, обозначаемое A Ç B , определяют как наибольшее нечеткое подмноже- ство, содержащееся одновременно в A и B.
(A Ç B) = ("x Î E : μAÇB ) = MIN(μA (x), μB (x)) .
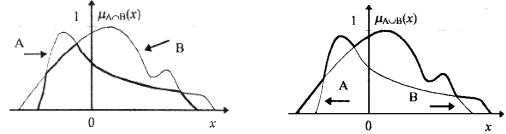
На рис. 4.2 графически представлено пересечение двух нечетких подмножеств.
Объединение. Объединение двух нечетких подмножеств A и B, A ÈB, определим как наименьшее нечеткое подмножество, которое со- держит как A, так и B:
(A È B) = ("x Î E : μ AÈB ) = MAX (μ A (x), μB (x)) .
На рис. 4.3 графически представлено объединение двух нечетких подмножеств.
Рис. 4.2. Пересечение двух |
Рис. 4.3. Объединение двух |
нечетких подмножеств |
нечетких подмножеств |
89
Дополнение. Будем говорить, что A и B – два нечетких подмноже- ства E дополняют друг друга, если
"x Î E : μA (x) = 1- μB (x).
Это обозначается следующим образом:
B = ¬A или A = ¬B .
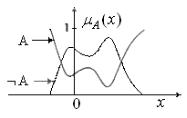
На рис. 4.4 представлено графически дополнение нечеткого под- множества A.
Дизъюнктивная сумма. Дизъюнктивная сумма двух нечетких подмножеств определяется в терминах объединений и пересечений сле- дующим образом [3]:
A Å B = (A Ç ØB) È (ØAÇ B) .
Рис. 4.4. Дополнение нечеткого
подмножества
Пример
A = {(x1 | 0,1),(x2 | 0,5),(x3 |1),(x4 | 0),(x5 | 0,8)}. B = {(x1 | 0,6),(x2 |1),(x3 | 0,4),(x4 | 0,7),(x5 | 0,8)}.
ØA = {(x1 | 0,9),(x2 | 0,5),(x3 | 0),(x4 |1),(x5 | 0,2)}. ØB = {(x1 | 0,4),(x2 | 0),(x3 | 0,6),(x4 | 0,3),(x5 | 0,2)}.
A Ç ØB = {(x1 | 0,1),(x2 | 0),(x3 | 0,6),(x4 | 0),(x5 | 0,2)}.
ØA Ç B = {(x1 | 0,6),(x2 | 0,5),(x3 | 0),(x4 | 0,7),(x5 | 0,2)}. A Å B = {(x1 | 0,6),(x2 | 0,5),(x3 | 0,6),(x4 | 0,7),(x5 | 0,2)}.
Разность двух подмножеств определяется соотношением
A - B = (A Ç ØB).
Используя данные, приведенные в предыдущем примере, получа-
ем
A - B = (A Ç ØB) = {(x1 | 0,1),(x2 | 0),(x3 | 0,6),(x4 | 0),(x5 | 0,2)}.
90
