Розділ 2 методологічні основи побудови гібридної інтелектуальної системи для вирішення основного класу задач data mining

2.1. Аналіз алгоритмів і методів кластеризації та регресії для вирішення класу задач Data Mining

Основна мета кластерного аналізу – знаходження груп схожих об’єктів у вибірці. Однак універсальність застосування привела до появи великої кількості несумісних термінів, методів і підходів, що утруднюють однозначне використання і несуперечливу інтерпретацію кластерного аналізу.

Виділяють три основних методи кластерного аналізу: деревоподібна кластеризація (дозволяє побудувати ієрархічне кластерне дерево), метод К-середніх (дозволяє досліднику перевірити статистичну значимість) та двовходове об’єднання (одночасна кластеризація об’єктів (стовпчиків) та спостережень (рядків). Після визначення з методом, необхідно обрати міру відстані між об’єктами та обчислити ці відстані. Розглянемо, які бувають міри відстаней між об’єктами.

Т

Моделі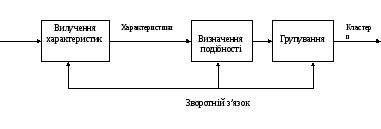

аким чином при кластеризації виокремлюють такі етапи, як (рис. 2.1): виділення характеристик; розбиття об’єктів на групи; представлення результатів.

Рис. 2.1. Загальна схема кластеризації

Алгоритми кластеризації поділяються на: ієрархічні та неієрархічні алгоритми.

Найбільшого поширення серед процедур прямої класифікації одержали ієрархічні алгоритми, які базуються на наступному визначенні кластера: всі відстані між об'єктами усередині групи повинні бути менше будь-якої відстані між об'єктами групи й іншою частиною множини об’єктів. (рис 2.2).

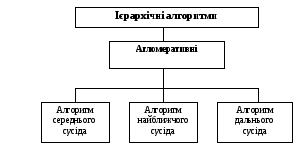
Рис. 2.2. Структура ієрархічних алгоритмів

Ієрархічні алгоритми дозволяють одержувати послідовну розбивку сукупності об’єктів за певним правилом. до них відносять агломеративні алгоритми, що працюють у зворотному порядку. Принцип роботи групи ієрархічних методів в вигляді дендрограми наведений на рис. 2.3.

Рис. 2.3. Принцип роботи групи ієрархічних методів

Ієрархічні алгоритми характеризуються рядом переваг у порівнянні з іншими процедурами кластерного аналізу. Відзначимо важливіші з них:

• відносна простота й змістовна ясність;

• допустимість втручання в роботу алгоритму;

• можливість графічного подання процесу класифікації у вигляді дендрограми, тобто дерева об'єднання (розбивки);

• порівняно невисока трудомісткість розрахунків.

Зупинимося докладніше на найбільш популярних процедурах прямої класифікації – ієрархічних агломеративних і деяких інших алгоритмах кластерного аналізу.

На першому кроці даних процедур кожний об'єкт вважається окремим кластером і провадиться об'єднання (агломерація) кластерів відповідно до деякого правила, що визначає послідовність (ієрархію) такого об'єднання. Алгоритми зазначеного типу розрізняються між собою, головним чином, критеріями, які використовуються при об'єднанні кластерів. Головні з них наступні:

1. Критерій „середнього сусіда” (центроїда). На кожному кроці поєднуються кластери К_p і К_s, відстань між центрами ваги яких мінімальна.

Даний критерій також має дві модифікації залежно від способу обліку чисельності кожного кластера: 1) критерій центроїда, розрахований без урахування числа об'єктів (статистичної ваги) поєднуваних груп (Unweigted pair-group centroid); 2) критерій центроїда, розрахований з урахуванням числа об'єктів (статистичної ваги) поєднуваних груп (Weigted pair-group centroid).

2. Критерій „найближнього сусіда”.(рис.2.4) В англомовній літературі даний критерій відомий як простий (одиночний) зв'язок (Single linkage). На кожному кроці поєднуються кластери К_p і К_s, відстань між найближчими об'єктами p і s яких мінімальна.

При його використанні на першому кроці поєднуються два найближчих між собою об'єкта, на другому – кластери за мінімальною відстанню між двома ближніми сусідами й т.д. Звідси й назва критерію: потрібний тільки один мінімальний зв'язок, щоб приєднати об'єкт до кластера, оскільки враховується лише одиночний, простий зв'язок з однією точкою кластера.

Рис. 2.4. Критерій «найблищого сусіда»

3. Критерій «далекого сусіда». (рис. 2.5). В англомовній літературі даний критерій відомий як повний зв’язок (Complete linkage). На кожному кроці поєднуються кластери К_p і К_s, відстань між найбільш віддаленими об'єктами p і s яких мінімальна.

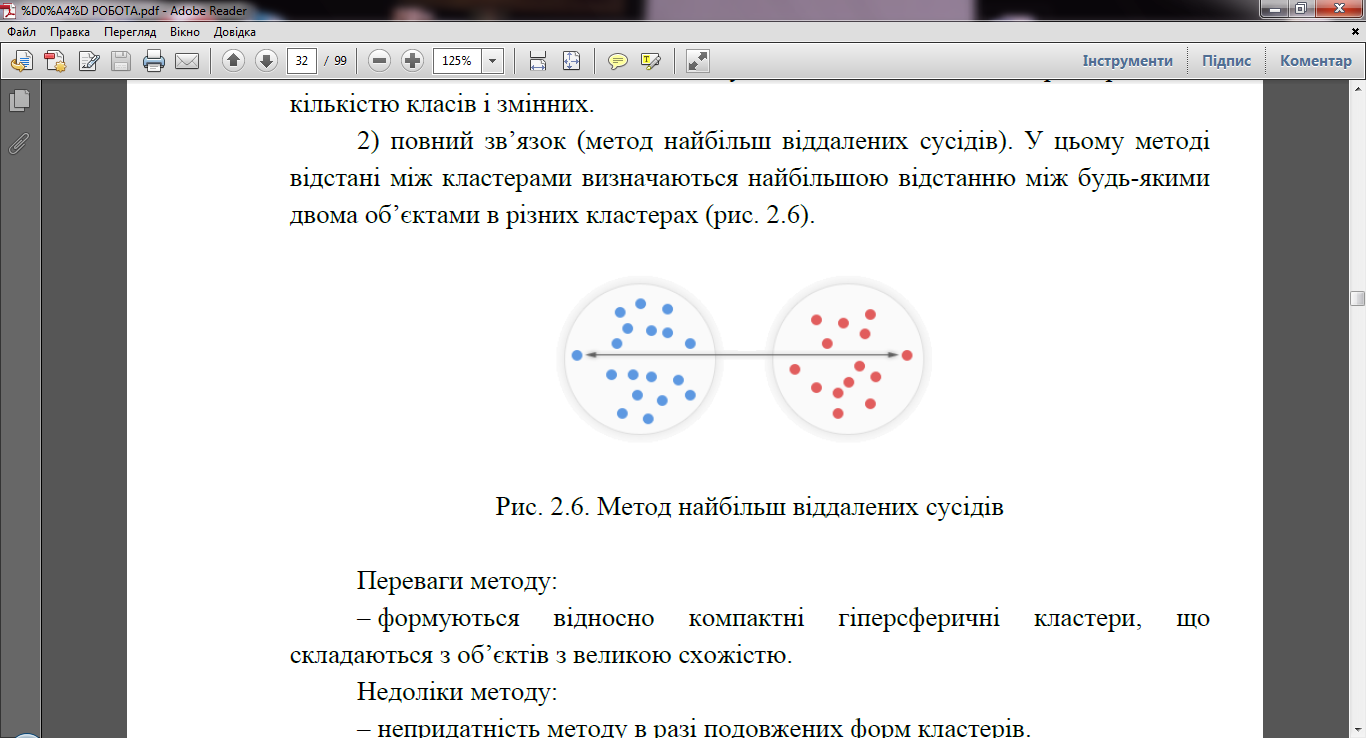
Рис. 2.5. Критерій „далекого сусіда”

4. Критерій «середнього зв’язку» (середньої відстані). На кожному кроці поєднуються кластери К_p і К_s, середня відстань між всіма парами об'єктів яких мінімальна.

Даний критерій має дві модифікації залежно від способу розрахунку середніх відстаней між об'єктами кожного кластера: 1) критерій середньої відстані, розрахований за формулою простої середньої арифметичної 2) критерій середньої відстані, розрахований по формулі зваженої середньої арифметичної. У першому випадку не враховується число об'єктів у кожному кластері, тобто їхня статистична вага, а в другому – враховується.

5. Критерій Уорда (Ward’s method). Цей метод агломерації відрізняється від попередніх тим, що він ґрунтується на аналізі збільшень внутрігрупової варіації чинників-симптомів для всіх можливих варіантів об'єднання кластерів. Помічено, що метод Уорда приводить до утворення кластерів приблизно рівних розмірів у формі гіперсфер.

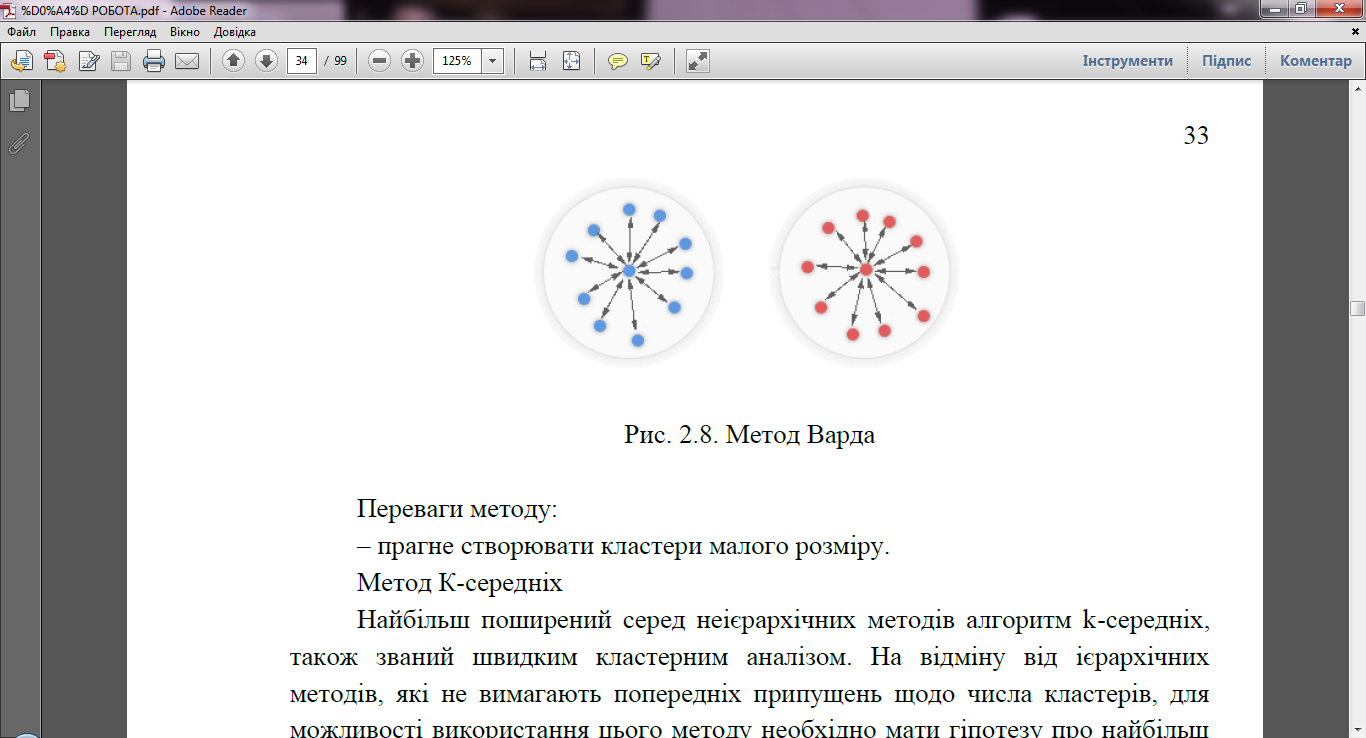
Рис. 2.6. Критерій Уорда

Загальна схема ієрархічного агломеративного алгоритму складається з п’яти основних етапів:

1) всі об’єкти z_i розглядаються як n самостійних кластерів К₁, К₂, … , К_n;

2) розраховуються відстані між всіма кластерами, і утворюються матриця відстаней D, розміру nn;

3) на базі обраного критерію визначається пара найближчих кластерів, які поєднуються в один новий кластер. Якщо відразу кілька кластерів мають мінімальну відстань між собою, то вибирають будь-яку пару;

4) обчислюються відстані від отриманого нового кластера до всіх інших. Розмірність матриці D при цьому знижується на одиницю;

5) на наступному кроці повторюється виконання пунктів 2, 3, 4 доти, поки не вийде розбивка, що складається з одного кластера – вихідної сукупності об'єктів (див. рис. 2.7).

Очевидно, що доводити ієрархічний агломеративний алгоритм до кінця не має змісту, тому що одержаний результат кластеризації є тривіальним, а завдання багатомірного групування залишається невирішеним. Необхідна об'єктивно обґрунтована зупинка процедури агломерації. Сигналом для такої зупинки може служити різкий ріст на черговому кроці мінімальної відстані між поєднуваними кластерами. Це вказує на те, що в одну групу поєднуються вже більш різнорідні об’єкти, чим на попередніх кроках.

Як видно із загальної блок-схеми наведеного алгоритму (рис. 2.6), для його успішного здійснення необхідно:

1. розрахувати відстані від нового (об’єднаного) кластера до всіх інших;

2. вчасно зупинити процедуру, вибравши оптимальне число компактних груп об'єктів.

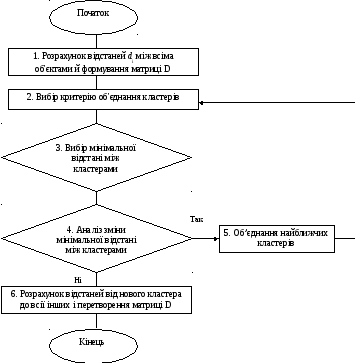
Рис. 2.7. Блок-схема ієрархічного алгоритму кластеризації

З приводу останньої проблеми можна сказати, що вона вирішується в значній мірі суб’єктивно, залежно від досвіду й інтуїції дослідника. На відміну від неї, перше завдання має цілком строге математичне рішення. Існує загальна формула для розрахунку відстані між кластером К_r, що є результатом об'єднання кластерів K_p і K_s, і кластером K_g.

Таким чином визначаються відстані від нового (об’єднаного кластера) до всіх інших. Потім відбувається перехід до третього етапу алгоритму з наступним аналізом зміни мінімальної відстані між кластерами. Зупинка багатовимірної процедури здійснюється в тому випадку, коли зазначена відстань зростає стрибкоподібно, що сигналізує про перспективу об'єднати в один кластер об’єкти, досить віддалені один від одного.

Неієрархічні алгоритми грунтуються на оптимізації деякої цільової функції, що визначає оптимальне в певному сенсі розбиття множини об’єктів на кластери.(рис 2.8) У цій групі популярні алгоритми сімейства k-середніх (k-means, fuzzy c-means, Густафсон-Кесселя), які в якості цільової функції використовують суму квадратів зважених відхилень координат об'єктів від центрів шуканих кластерів. Кластери шукаються сферичної або еліпсоїдної форми. У канонічній реалізації мінімізація функції проводиться на основі методу множників Лагранжа і дозволяє знайти тільки найближчий локальний мінімум. Серед неієрархічних алгоритмів, не базованих на відстані, слід виділити EM-алгоритм (Expectation-Maximization). У ньому замість центрів кластерів передбачається наявність функції щільності ймовірності для кожного кластеру з відповідним значенням математичного очікування і дисперсією.

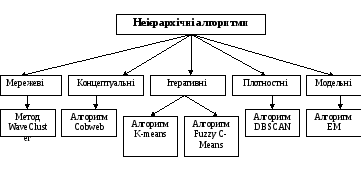Рис.2.8. Класифікація неієрархічних алгоритмів

Найбільш поширений серед неієрархічних методів алгоритм k-середніх (k-means), також званий швидким кластерним аналізом.

Алгоритм k-середніх будує k кластерів, розташованих на можливо великих відстанях один від одного. Основний тип завдань, які вирішує алгоритм k-середніх – наявність припущень (гіпотез) щодо числа кластерів, при цьому вони повинні бути різні настільки, наскільки це можливо. Вибір числа k може базуватися на результатах попередніх досліджень, теоретичних міркуваннях або інтуїції.

Загальна ідея алгоритму: задане фіксоване число k кластерів спостереження співставляються кластерам так, що середні в кластері (для всіх змінних) максимально можливо відрізняються один від одного.

Опис алгоритму:

1. Початковий розподіл об’єктів по кластерах. Вибирається число k, і на першому кроці ці точки вважаються „центрами” кластерів. Кожному кластеру відповідає один центр.

Вибір початкових центроїдів може здійснюватися таким чином:

–  вибір k-спостережень для максимізації початкової відстані;

–  випадковий вибір k-спостережень;

–  вибір перших k-спостережень.

У результаті кожен об'єкт призначений певному кластеру.

2. Ітератівний процес.

Обчислюються центри кластерів, якими потім і далі вважаються покоординатні середні кластерів. Об'єкти знову перерозподіляються.

Процес обчислення центрів і перерозподілу об'єктів продовжується до тих пір, поки не виконана одна з умов:

• кластерні центри стабілізувалися, тобто всі спостереження належать кластеру, якому належали до поточної ітерації;

• число ітерацій дорівнює максимальному числу ітерацій.

На рис.2.9 наведено приклад роботи алгоритму k-середніх для k, рівного двом.

Рис 2.9. Робота кластерного аналізу

Після отримання результатів кластерного аналізу методом k-середніх слід перевірити правильність кластеризації (тобто оцінити, наскільки кластери відрізняються один від одного). Для цього розраховуються середні значення для кожного кластера. При гарній кластеризації повинні бути отримані сильно відрізняються середні для всіх вимірювань або хоча б більшої їх частини.

Також ще одним з найпопулярніших алгоритм кластеризації з автоматичним вибором числа кластерів є G-means . У його основі лежить припущення про те, що кластерізуемие дані підпорядковуються деякого унімодальних закону розподілу, наприклад гауссовскому. Тоді центр кластера, який визначається як середнє значень ознак потрапили в нього об'єктів, може розглядатися як мода відповідного розподілу.

Якщо вихідні дані описуються унімодальних гауссовским розподілом із заданими середнім, то можна припустити, що всі вони відносяться до одного кластеру.

Якщо розподіл даних не гауссовское, то виконується поділ на два кластери. Якщо в цих кластерах розподілу виявляться близькі до гауссовскому, то в першому наближенні вважається, що k = 2 буде оптимальним. В іншому випадку будуються нові моделі з великим числом кластерів, і так до тих пір, поки розподілення у кожному з них не виявиться достатньо близьким до гауссовскому. Така модель і, відповідно, число кластерів в ній будуть вважатися оптимальними.

Алгоритм G-means є ітеративним, де на кожному кроці за допомогою звичайного алгоритму k-means будується модель з певним числом кластерів (початкове значення k вибирається рівним 1), яке збільшується на кожній ітерації. Збільшення k проводиться за рахунок розбиття кластерів, в яких дані не відповідають гауссовскому розподілу.

Алгоритм «приймає рішення» про подальше розбитті на основі статистичного тесту даних, пов’язаних з кожним центроїдом. Якщо при цьому буде виявлено, що вони розподілені по гауссовскому законом, то подальшого сенсу в їх розбитті немає. Фактично в процесі роботи G-means алгоритм k-means буде повторений k раз, тому складність алгоритму становить O ( k ).