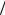
1.15. Электрон в бесконечно глубокой яме

Для бесконечного пространства энергия (1.14.5) и волновой вектор (1.14.6) являются непрерывной функцией. Это означает, что энергия и импульс (по направлению и абсолютной величине) могут принимать любые значения. Математически такая ситуация возникает из-за того, что формально бесконечное пространство не накладывает на решение граничных условий.

Электрон в твердом теле можно грубо представить как объект, находящийся в трехмерной потенциальной яме с глубиной порядка работы выхода (обычно, несколько эВ). Для любых наноразмерных структур ключевую роль играет наличие границ. Граничные условия, накладываемые на волновую функцию, приводят к тому, что импульс (и, соответственно, энергия) может принимать только дискретные значения, либо значения в некотором диапазоне. В этом случае говорят об эффектах размерного квантования в квантовых ямах.

Рассмотрим модель электрона в одномерной бесконечно глубокой яме, где U (x)= 0 при 0 < x < L и U (0)=U (L)= ∞ . Общее ре-

и эта задача отличается от случая бесконечного пространства только накладываемыми граничными условиями

причем строгое равенство нулю имеет место для формально бесконечной глубины потенциальной ямы. Из граничных условий (1.15.2) очевидно, что b = 0 и волновой вектор (и длина волны) может принимать только дискретные значения, определяемые условием

Вспоминая определение волнового вектора (1.13.2), получаем, что (1.15.3) эквивалентно тому, что на длине ямы может умещаться только целое число полуволн

27

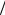
Тогда волновые функции и собственные значения энергии для разного значения n (т. н. квантового числа) будут иметь вид

а энергия основного состояния (т.е. состояния с минимальной энергией) электрона в яме будет соответствовать волновой функции с одной полуволной на длину ямы (n =1) со значением в кремнии

где m0 – масса электрона в пустоте.

Константу a (1.15.5) можно определить с помощью условия нормировки волновой функции:

644=7L / 2448

Тогда состояние электрона на n-ом уровне описывается волно-

Волновые функции электронов трехмерной задачи с нулевыми граничными условиями записываются с помощью тройки независимых целочисленных квантовых чисел nx ,ny ,nz (ср. (1.15.7) и

(1.15.5):

28

Если расстояние между ближайшими энергетическими уровнями оказывается меньше kBT , то уровни «размываются», и размер-

ное квантование становится несущественным. Например, кубик металла с объемом Ω = 1мкм3 слишком велик, чтобы там было заметно влияние размерного квантования. Действительно, концентрация электронов в металлах Nat ~ 1022 см-3, и металл можно

представить как потенциальную яму глубиной ~ 5 эВ, причем на каждом уровне находится два электрона с разными спинами. Тогда среднее расстояние между уровнями ~ 5эВ/ NatΩ ~ 10-10 эВ <<

<< kBT .

29

1.16. Плотность дискретного и непрерывного спектра двумерной системы

Рассмотрим задачу о количестве разрешенных состояний двумерной системы с энергией, меньшей некоторого значения ε для наноразмерных образцов (т.е. с учетом квантования).

Для простоты рассмотрим квадратную систему Lx = Ly = L :

Параметры nx и ny , принимающие целочисленные положи-

тельные значения, имеют смысл количества полуволн, укладывающихся на соответствующей грани прямогуольной двумерной системы. Состояние электрона с самой низкой энергией описывается квантовыми числами

(nx , ny )= (1,1),

Равенство энергий для разных состояний называется вырождением по энергиям. В данном случае оно носит случайный характер, поскольку обусловлено квадратностью системы. Следующим по величине энергии будет невырожденный уровень E22 = 8ε0 с энер-

гией ниже, чем у двух вырожденных уровней E13 = E31 =10ε0

(рис.1.4).

В этом случае легко подсчитать количество состояний с энергией, меньшей некоторой заданной энергии ε . Действительно, удвоенное (из-за наличия спина) количество квадратиков в четверти

30