
Kniga_16_Fizicheskie_osnovy_nanoinzhenerii-1
.pdf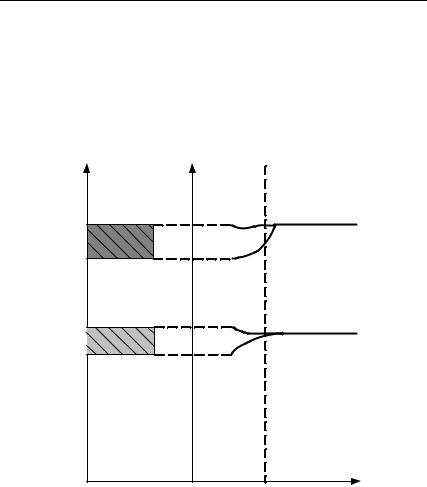
Конспект лекций |
|
33 |
Расчеты показывают, что при b равном единицам ангстрем τ |
||
очень мало: ~10–15 с. Тогда из соотношения неопределенностей |
||
dE dt ≥ h следует, что при уменьшении времени пребывания элек- |
||
трона в заданном состоянии увеличивается интервал энергии этого |
||
состояния, чему соответствует образование для электронов разре- |
||
шенных зон (рис. 1.4). Наименьшее τ |
будет при этом у внешних |
|
электронов, и они становятся обобществленными. Более глубинные |
||
электроны имеют большее значение τ и меньшее dE. |
|
|
E |
|
|
|
E2 |
|
|
E1 |
|
0 |
a |
r |
Рис. 1.4. Образование разрешенных энергетических зон |
||
при сближении атомов |
|
|
Таким образом, каждому энергетическому уровню изолированного атома в кристалле соответствует зона разрешенных энергий. Зоны разрешенных энергий разделены запрещенными зонами. С увеличением энергии электрона в атоме ширина разрешенных зон увеличивается, а ширина запрещенных уменьшается. В общем случае зоны, образованные отдельными уровнями, могут перекрываться, образуя гибридную зону.
34 |
Физические основы наноинженерии |
Приближение слабой связи. Энергетический спектр электронов в кристалле, как было показано выше, имеет зонный характер. Определим, как энергия электронов зависит от импульса p. Рас-
смотрим свободные электроны, движущиеся в периодическом поле кристаллической решетки. В этом случае уравнение Шредингера решают при циклических граничных условиях:
∂2Ψ + 2m (E −u)Ψ = 0.
∂x2 2
Решение этого уравнения по Блоху можно записать в виде
Ψ(x) = u1 (x)eikx ,
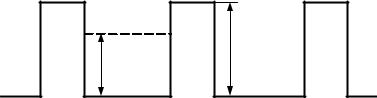
где u1 (x) – периодическая функция, период которой совпадает с периодом потенциала u (x), т. е. равен d (d = a +b, где a – ши-
рина потенциальной ямы; b – ширина потенциального барьера согласно модели Кронига–Пенни (рис. 1.5)).
u
E
Рис. 1.5. Модель Кронига–Пенни
Можно показать, что с учетом граничных условий, подставляя решение по Блоху в уравнение Шредингера, получим уравнение
mab u |
sin (αa) |
+cos(αa) = cos(ka), |
(1.12) |
||||
|
|||||||
2 |
αa |
|
|
|
|
||
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2mE 2 |
|
|
|||
|
α = |
|
|
. |
(1.13) |
||
|
2 |
||||||
|
|
|
|
|
|
|
|
Если барьеры весьма высокие и тонкие, то можно |
принять |
||||||
a ≈ d. Обозначим левую часть уравнения (1.12) через y(αa): |
|||||||
y(αa) = mab u |
sin (αa) |
+cos(αa). |
(1.14) |
||||
|
|||||||
|
2 |
|
|
αa |
|
|
|
|
|
|
|
|
|
|
|
Конспект лекций |
35 |
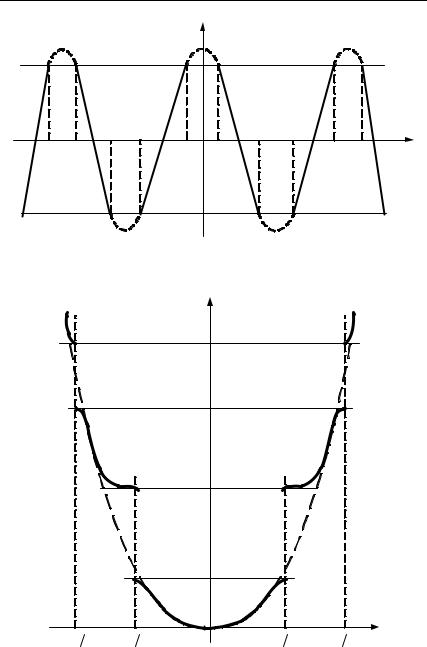
Уравнение (1.14) решаем графическим способом (по оси абсцесс откладываем αa, а по оси ординат y(αa)). Качественно получаем характеристику, изображенную на рис. 1.6. Пунктиром нанесена часть кривой y(αa), выходящая за ±1. Эта часть кривой не может удовлетворять уравнению (1.12), поскольку cos(ka) не может быть по абсолютному значению больше 1. Сплошной линией нанесена часть кривой y(αa), лежащая в пределах ±1 и удовле-
творяющая уравнению (1.14). Участки на оси абсцисс AB, CD, A1B1 и C1D1, на которых кривая не выходит за пределы
±1, соответствуют разрешенным зонам энергии, поскольку α и E связаны соотношением (1.13). При αa → 0 имеем sin (αa)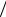 αa →1,
αa →1,
y(αa)>1, |
точка A определяется таким углом αa, при котором |
|
y(αa)=1. |
В точке B |
y(αa) достигает –1, следовательно, αa = π. |
От точки |
B до точки |
C наблюдается запрещенная зона. Затем |
разрешенная зона CD. B D αa = 2π. Кривая y(αa) симметрична
относительно нуля, следовательно, при отрицательном αa имеем аналогичные отрицательные углы. Ширина разрешенных зон уве-
личивается по мере роста αa. Из (1.12) следует, |
что в точке B |
||
cos(ka)= −1, следовательно, ka = π. В точке D |
имеем ka = 2π |
||
и т. д. Потолки разрешенных зон наблюдаются при условии: |
|||
k = |
nπ |
, |
(1.15) |
|
|||
|
a |
|
|
где n =1,2,3,….
На рис. 1.7 приведена кривая E (k ), соответствующая рассматриваемому случаю. Вблизи дна первой разрешенной зоны кривая E (k ) представляет собой параболу. Однако к потолку зоны кривая E (k ) отклоняется от параболы. При k = ±π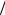 a имеем потолок
a имеем потолок
первой зоны и разрыв кривой, соответствующий запрещенной зоне. Далее имеются отрезки кривых, обусловленные более высокими разрешенными энергетическими зонами.
Таким образом, волновые законы движения электронов в периодическом потенциальном поле приводят к возникновению разрешенных и запрещенных зон энергии.
36 |
|
|
|
Физические основы наноинженерии |
|||
|
|
|
y(αa) |
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
−2π |
|
−π |
π |
|
2π |
αa |
D1 |
C1 |
B1 |
A1 |
A |
B C |
D |
|
|
|
|
−1 |
|
|
|
|
|
|
Рис. 1.6. Зависимость |
y(αa) |
|
|
||
|
|
|
E |
|
|
|
|
D1 |
|
|
|
|
|
D |
|
C1 |
|
|
|
|
|
C |
|
|
B1 |
|
|
|
B |
|
|
−2π a |
−π a |
0 |
|
π a |
2π a k |
|
|
Рис. 1.7. Зависимость энергии электрона от волнового вектора k |
|||||||

Конспект лекций |
37 |
1.3.2. ЗОНЫ БРИЛЛЮЭНА
Ранее использовалось понятие пространства импульсов, которое определялось путем задания составляющих импульсов в декартовой системе координат. Модуль волнового вектора, или вол-
новое число равно k = 2π λ, а λ = h p |
– длина волны де Бройля. |
Тогда p = k; если нет , то p = hk 2π, |
где = h 2π. |
Следовательно, импульс пропорционален волновому вектору k : p = k; тогда вместо пространства импульсов можно рассматри-
вать k-пространство, задаваемое составляющими kx , ky , kz . Раз-
решенным энергетическим зонам в твердом теле соответствуют зоны в k-пространстве. Области значений волнового вектора k,
в пределах которых энергия электрона E (k ), являющаяся периоди-
ческой функцией k, испытывает полный цикл своего изменения, называют зонами Бриллюэна. На границах зон энергия претерпевает разрыв. Для одномерного кристалла первая зона Бриллюэна простирается от k = −π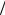 a до k = π
a до k = π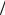 a и имеет протяженность 2π
a и имеет протяженность 2π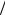 a
a
(см. рис. 1.7).
Как уже указывалось, из решения уравнения Шредингера для электрона, находящегося в периодическом потенциальном поле кристаллической решетки, следует, что собственные значения (разрешенные) энергии электрона должны быть периодическими функциями k :
E (kx )= E (kx ± n2π ax ). |
(1.16) |
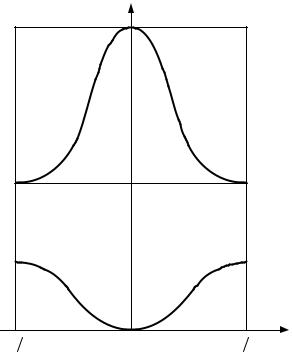
Кривая E (kx ) называется дисперсионной кривой. Как видно из рис. 1.8, для каждой из разрешенной зон справедливо соотношение (1.16), хотя кривые E (kx ) для разрешенных зон отличаются друг
от друга. С ростом E ширина разрешенных зон увеличивается. Если отрезок CD сдвинуть на 2π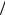 ax влево, а отрезок C1D1 на
ax влево, а отрезок C1D1 на
2π ax вправо, то вторую зону Бриллюэна можно привести к первой. Первую зону Бриллюэна, куда перенесены E (kx ) для разных энергетических зон, называют приведенной зоной Бриллюэна
ax вправо, то вторую зону Бриллюэна можно привести к первой. Первую зону Бриллюэна, куда перенесены E (kx ) для разных энергетических зон, называют приведенной зоной Бриллюэна

38 |
|
|
Физические основы наноинженерии |
||
(рис. 1.9). В дальнейшем будут преимущественно рассматриваться |
|||||
лишь две верхние разрешенные энергетические зоны. Верхняя |
|||||
разрешенная зона называется зоной проводимости, а нижняя – ва- |
|||||
лентной зоной. |
|
|
|
|
|
D1 |
|
E |
|
D |
|
|
|
|
|
||
|
C1 |
|
C |
|
|
|
B1 |
|
B |
|
|
|
|
A |
|
|
|
−2π a |
−π a |
0 |
π a |
2π a |
k |
Рис. 1.8. Зависимость энергии электрона от волнового вектора k |
|||||
|
для разных энергетических зон |
|
|
||
В реальных кристаллах направления составляющих волнового вектора k выбирают в соответствии с определенными кристалло-
графическими направлениями. Зависимости E (k ) у реальных
кристаллов являются достаточно сложными.
В качестве примера рассмотрим зонную структуру кремния для двух направлений в k-пространстве. Минимум зависимости E (k )
Конспект лекций |
39 |
или дисперсионной кривой называют дном энергетической зоны, а максимум – потолком зоны. Как видно из рис. 1.10, дно зоны проводимости у кремния находится не в середине зоны Бриллюэна, а вблизи ее границы в направлении «[100]». Вершина валентной зоны расположена в середине зоны Бриллюэна.
|
E |
|
−π a |
π a |
k |
|
Рис. 1.9. Приведенная зона Бриллюэна |
|
Минимальный зазор между валентной зоной и зоной проводимости принимается за ширину запрещенной зоны Eg .
При упрощенном рассмотрении энергетической структуры полупроводников вместо истинных дисперсионных кривых E (k ),
ограничивающих валентную зону и зону проводимости, проводят две параллельные прямые: одну – касательную к дну зоны проводимости, вторую – касательную к вершине валентной зоны. Первую прямую принимают за нижнюю границу (дно) зоны проводимости, вторую – за верхнюю границу (потолок) валентной зоны.
40 |
|
|
Физические основы наноинженерии |
|
E |
|
|
E |
|
|
EC |
C |
|
|
|
1,1 эВ |
|
|
Eg |
EV |
|
|
EV |
|
|
k = [000] |
|
[111] |
0 |
[100] |
k |
|
Рис. 1.10. Зонная структура кремния |
||
1.3.3. ЭФФЕКТИВНАЯ МАССА ЭЛЕКТРОНА
Известно: p = k = mv,
v = |
|
k. |
(1.17) |
m |
Кинетическая энергия свободного электрона Ek = E:
E |
= |
|
mv2 |
. |
|
|
|||||
k |
2 |
|
|
||
|
|
|
|||
Подставим (1.17), тогда |
|
|
|
|
|
E |
= |
2k 2 |
. |
||
|
|||||
k |
|
|
2m |
||
|
|
|
|||
Конспект лекций |
|
|
|
|
|
|
41 |
||
Продифференцируем Ek по k : |
|
|
|||||||
|
dEk |
= |
|
π2 k, |
|
||||
|
|
|
|
|
|
||||
|
|
dk |
|
|
|
m |
|
||
отсюда |
|
|
|
|
|
|
|
||
k = |
m |
dE . |
(1.18) |
||||||
2 |
|
||||||||
|
|
|
|
|
dk |
|
|||
Подставим (1.18) в (1.17): |
|
|
|
|
|
|
|
||
v = |
|
|
k = |
1 dE . |
(1.19) |
||||
m |
|||||||||
|
|
|
|
|
dk |
|
|||
Формула (1.19) справедлива не только для свободного электрона, но и для электрона, находящегося в потенциальном поле.
Пусть энергия зонного электрона изменяется под некоторым внешним воздействии:
dE = Fv dt, |
(1.20) |
|||
где F – внешняя сила. |
|
|
|
|
Подставим (1.19) в (1.20): |
|
|
|
|
dE = |
F |
dE dt, |
|
|
|
|
|||
|
|
|
dk |
|
отсюда |
|
|
|
|
dk |
= F . |
(1.21) |
||
dt |
|
|
|
|
Продифференцируем (1.19) по времени:
dv |
= |
1 |
|
d dE |
= |
1 |
|
d 2E |
|
dk |
. |
|||
dt |
|
|
|
|
|
dk |
2 |
dt |
||||||
|
|
|
||||||||||||
|
|
|
dt |
dk |
|
|
|
|
|
|
||||
Подставим (1.21) в (1.22):
dv |
= |
F |
d 2E |
= a, |
dt |
|
|||
|
2 |
dk2 |
|
(1.22)
(1.23)
где a – ускорение.
Формула (1.23) связывает ускорение и силу, т. е. она выражает второй закон Ньютона F = ma; a = F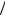 m.
m.
Из (1.23) следует, что под действием внешней силы электрон в периодическом поле кристалла движется так, как двигался бы свободный электрон, обладающий массой
42 |
|
|
Физические основы наноинженерии |
||
* |
|
|
1 |
|
|
m |
= |
|
|
. |
(1.24) |
1 |
d 2E |
||||
|
2 |
dk2 |
|
||
Масса m* называется эффективной массой электрона. Приписывая электрону, находящемуся в периодическом поле кристалла,
массу m*, можно считать этот электрон свободным и описывать
его движение во внешнем поле так, как описывается движение свободного электрона. Эффективная масса, отражающая особенности движения электрона в периодическом поле, является своеобразной функцией. Она может быть как положительной, так и отрицательной, а по абсолютному значению как меньше, так и больше массы покоя электрона. Эффективная масса свободного электрона равна массе покоя.
При движении электрона в периодическом потенциальном поле кристалла работа внешней силы может переходить как в кинетическую, так и потенциальную энергию электрона:
A = Ek + u.
Если часть работы внешней силы, F = −qε, переходит в потен-
циальную энергию, то скорость электрона возрастает медленнее, чем у свободного электрона и, следовательно, его эффективная масса больше массы покоя. Если вся работа внешней силы переходит в потенциальную энергию, то скорость электрона изменяться не будет, и он будет вести себя, как частица с бесконечно большой массой.
В потенциальную энергию может переходить не только работа внешней силы, но и кинетическая энергия электрона. Скорость электрона будет в этом случае уменьшаться, т. е. он ведет себя как частица с отрицательной массой.
Возможен случай, когда в кинетическую энергию может переходить не только работа внешней силы, но и потенциальная энергия, тогда скорость электрона будет расти быстрее, чем у свободного, т. е. его эффективная масса будет меньше массы покоя.
На рис. 1.11 показаны зависимости E, v, m* от волнового век-
тора k. Вблизи дна разрешенной зоны энергия m* электрона положительна, а у потолка зоны – отрицательна. Точка A – точка перегиба зависимости E (k ), в этой точке dE dk достигает мак-
dk достигает мак-
