Методические указания

Дисперсионный анализ предназначен для выявления влияния отдельных факторов на результирующий показатель. В зависимости от числа факторов дисперсионный анализ бывает однофакторным, двухфакторным и многофакторным. Однако, начиная с трехфакторного анализа, имеет место большое разнообразие различных воздействий факторов, что усложняет интерпретацию полученных результатов.

Предлагается, что на каждом уровне фактора А_j (j=1,m) результативный признак подчиняется нормальному распределению с одинаковыми дисперсиями.

Выдвигается нулевая гипотеза на уровне значимости α о равенстве групповых средних по всем уровням: H₀: μ₁=μ₂=…=μ_m.

Суть метода дисперсионного анализа заключается в переходе от проверки нулевой гипотезы. Н₀ а равенстве групповых средних к проверке. Н₀ о равенстве факторной и остаточной дисперсий.

Требуется исследовать влияние фактора A на признак Х. Экспериментальные данные в общем виде записывают в таблицу:

№ п/п измерения	Уровни фактора A
	А1	А2	…	Аm
1	x11	x12	…	x1m
2	x21	x22	…	x2m
4	…	…	…	…
…			…
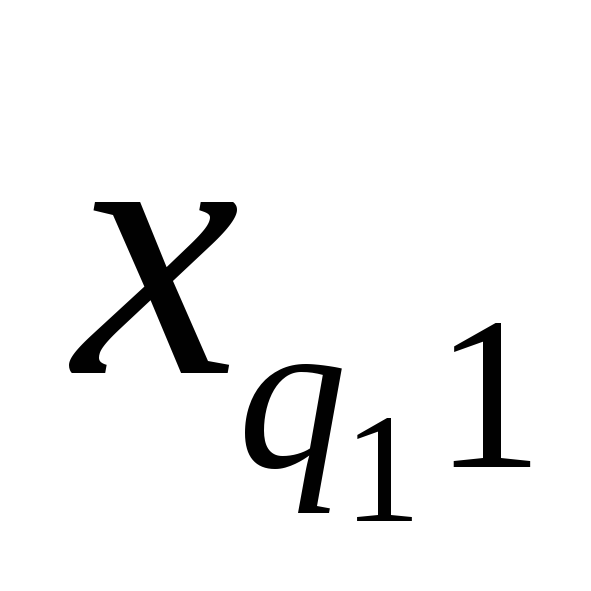
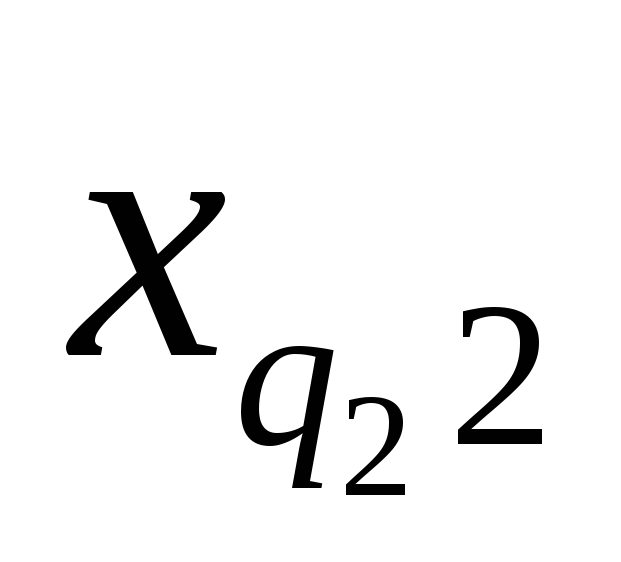
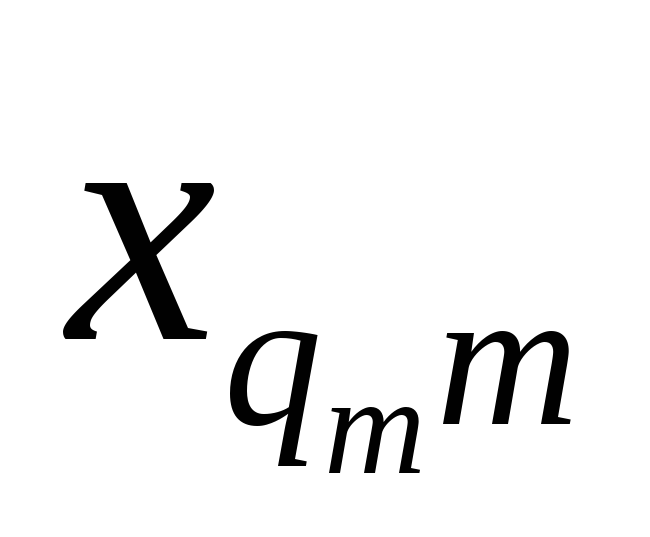
qj	q1	q2	…	qm
Rj			…
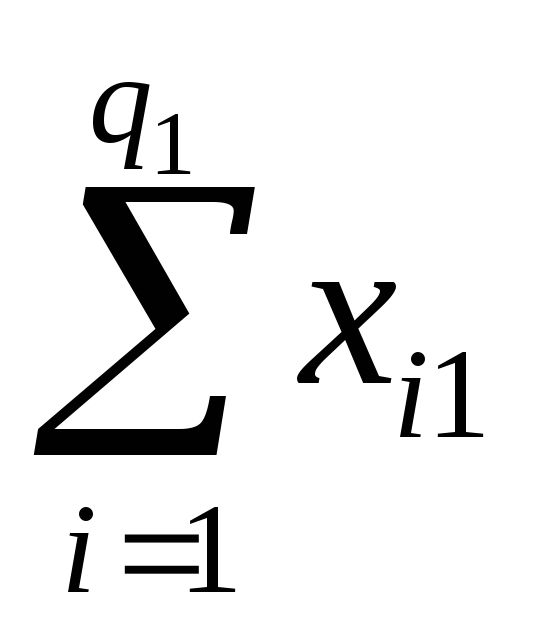
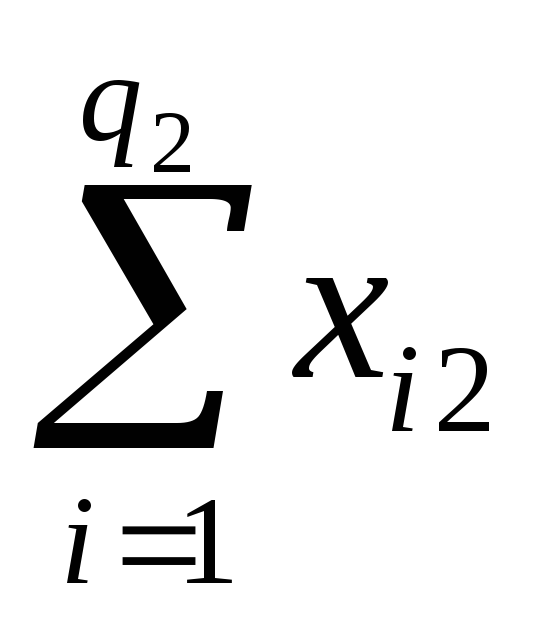
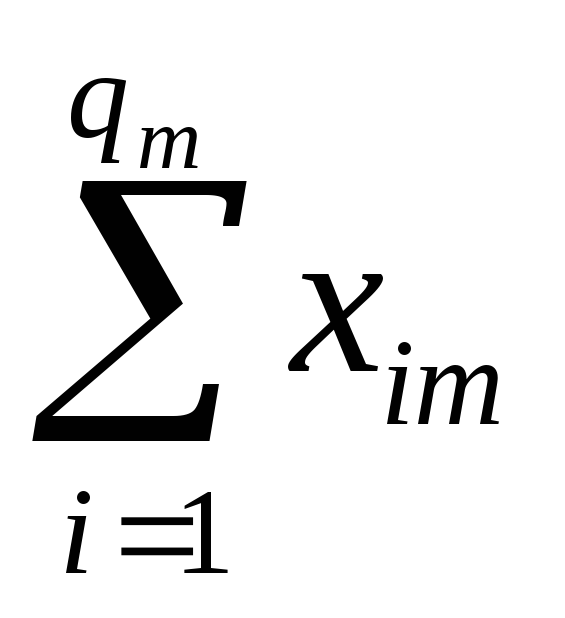
Pj			…

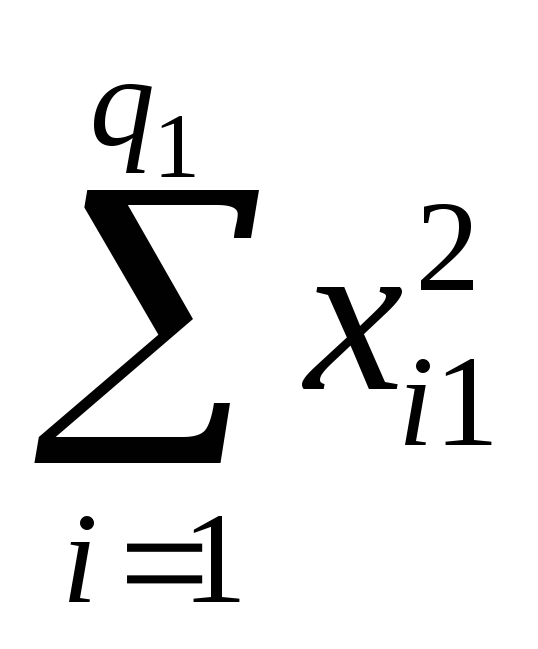
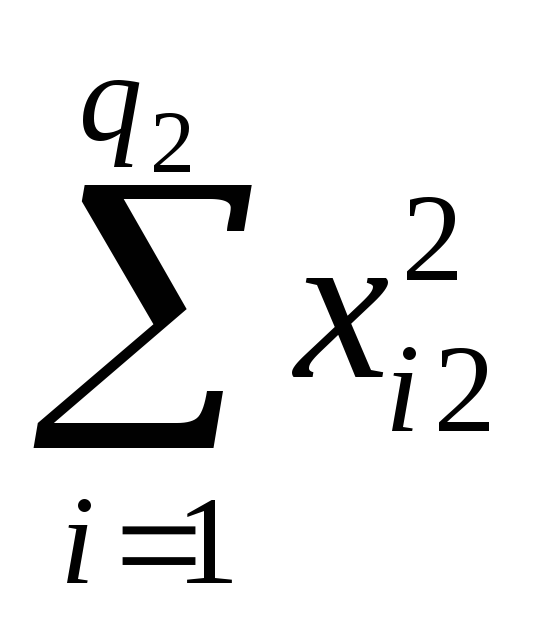
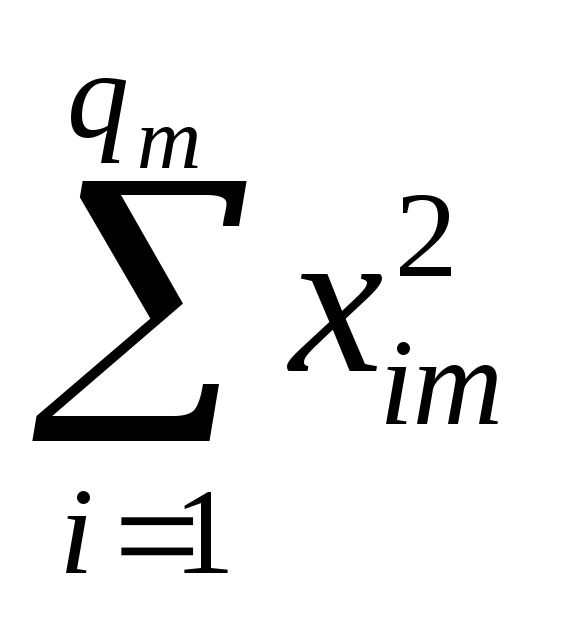
N=, q_j – число испытаний на j-ом уровне (j=1,2, … ,m)

R_{j =}-сумма значений Х наj-ом уровне

P_j =- сумма квадратов значений величины Х наj-ом уровне.

Проверка равенства дисперсий на всех уровнях фактора A.

Проверим гипотезу о равенстве дисперсий на всех уровнях, т.е. Н₀:.

Для равномерного статистического комплекса используем критерий Кочрена и найдем наблюдаемое значение критерия:

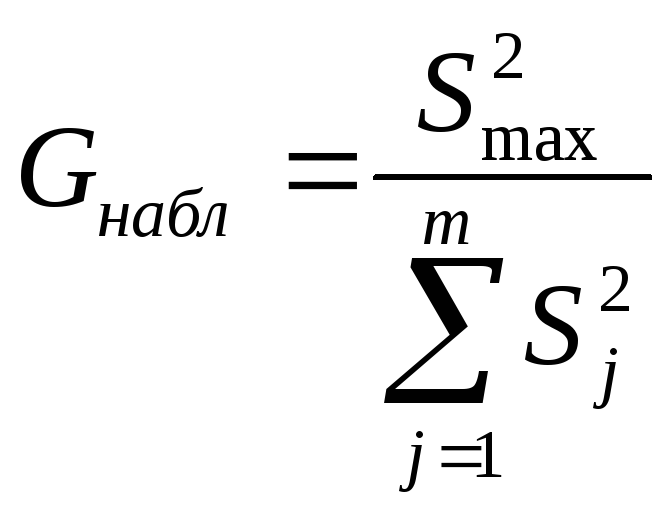
где - наибольшая из исправленных оценок дисперсий по всей уровням.

По таблицам G–распределения для уровня значимости α, числа сравниваемых совокупностей m и числа степеней свободы =n-1 (n – объем выборки для уровня с максимальной дисперсией) находим G_табл.(α; m; n-1). Если G_набл.<G_табл., то гипотеза о равенстве дисперсий не отвергается.

При неодинаковом числе испытаний на уровнях (неравномерный статистический комплекс) гипотеза о равенстве дисперсий на всех уровнях проверяется с помощью критерия Бартлетта: , где

; ;

.

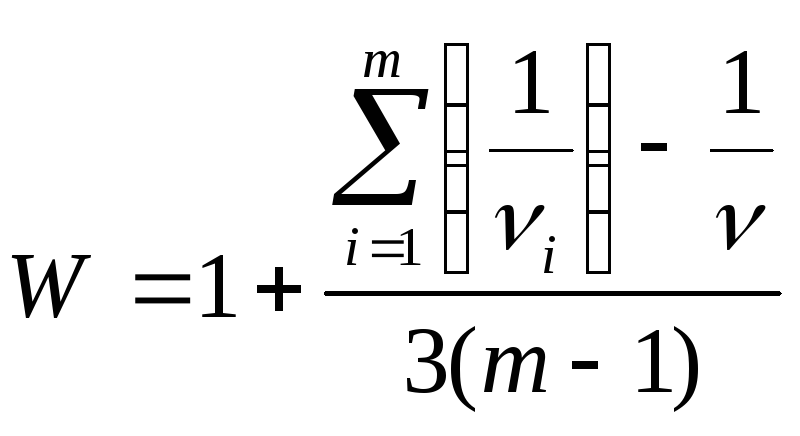Полученное значение сравнивают с критическим B_табл(; m-1). Правило принятия гипотезы: если B_набл<B_табл, то принимается нулевая гипотеза.

Вычисление дисперсий.

По данным вычислениям R_j и P_j и находим факторную и остаточную дисперсии по формулам:

; .

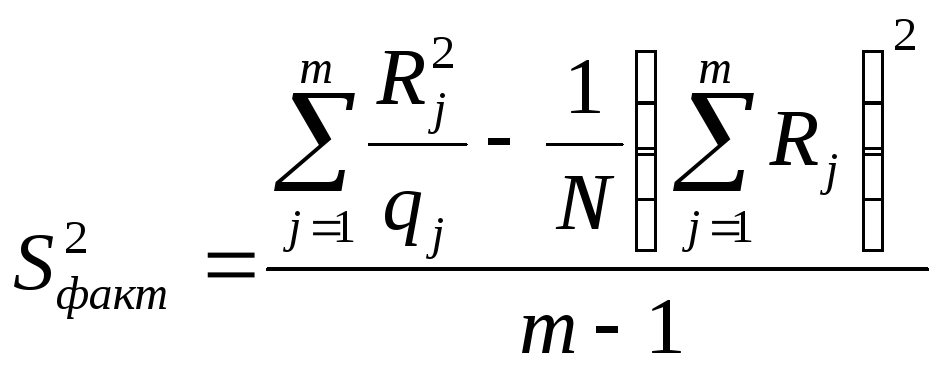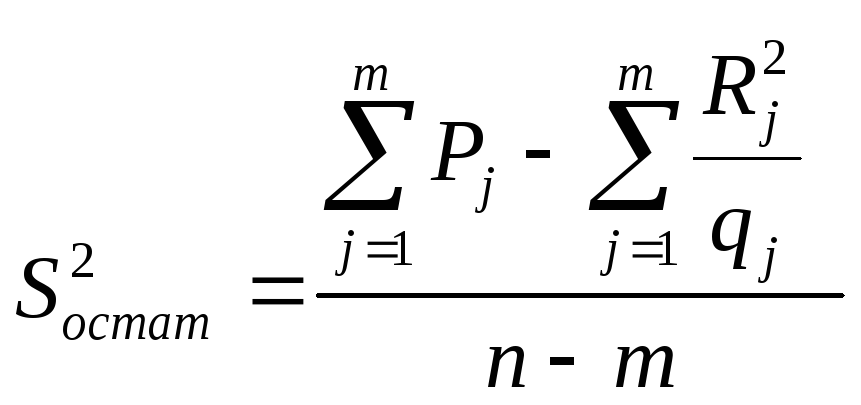где f₁=m-1 – число степеней свободы по уровням; f₁=n–m – число степеней свободы для остаточной дисперсии.

Принятие гипотезы.

Для проверки гипотезы о влиянии фактора A вычислим наблюдаемое значение критерия Фишера-Снедекора:

По таблице F–распределения находим критическое значение F=F_кр(α;f₁;f₁).

Если F_набл<F_табл., то нулевая гипотеза не отвергается и делается вывод о несущественном влиянии фактора A на признак Х, в противном случае Н₀ с вероятностью ошибки α отвергается, что доказывает влияние фактора А на величину Х.

5) Случай равномерного статистического комплекса.

В случае одинакового числа испытаний на всех уровнях q₁=q₂=…=q_m=q формулы для нахождения иупрощаются:

;

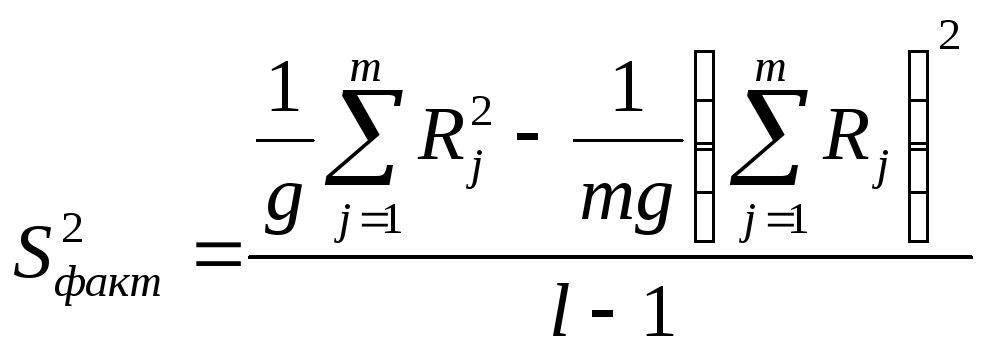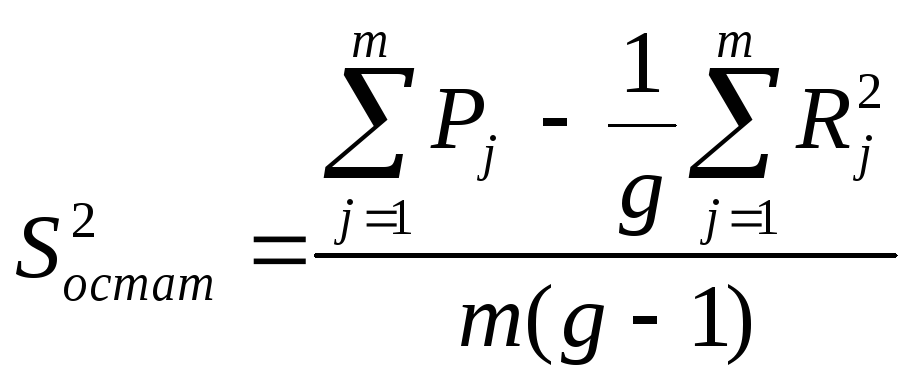
Задача 8 Варианты задачи даны в таблице с указанием результативного у и факторных x_1, x₂ признаков.

Номер варианта	Результативный признак	Факторные признаки
1	Y1	X1, X2
2	Y2	Х11, Х12
3	Y1	X11 X13
4	Y2	X10, X11
5	Y2	X9, X10
6	Y1	X3, X4
7	Y2	X9, X11
8	Y2	X11, X12
9	Y1	X3, X5
10	Y2	X11, X13

В следующей таблице представлены выборочные данные по показателям состояния личности у руководителей мужчин и женщин.

№	Y1	Y2	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11	X12	X13	X14
1	12	13	0,33	0,6	1,11	0,54	0,20	0,55	0,33	0,17	0,1	0,11	0,20	0,1	0,17	0,10
2	15	30	0,33	0,2	0,44	0,31	0,20	0,54	0,50	1,25	0,7	1,78	1,62	1,2	1,17	1,33
3	9	21	0,17	0,6	0,33	0,10	0,10	0,59	0,17	0,24	0,4	0,67	0,54	0,3	0,83	0,17
4	6	14	0,23	0,3	0,67	0,15	0,20	0,33	0,50	0,50	0,6	0,33	0,08	0,3	0,50	0,17
5	20	42	0,83	0,4	1,33	0,15	0,60	0,38	1,17	1,75	2,3	2,56	2,54	2,4	2,00	2,33
6	9	37	0,75	0,6	0,56	0,15	0,50	0,17	0,32	2,17	1,7	1,00	1,31	1,6	1,33	1,00
7	17	23	0,92	0,9	1,11	0,92	0,40	0,33	1,33	1,08	0,7	1,22	0,69	0,9	0,67	1,00
8	12	17	0,42	0,4	0,33	0,15	0,10	0,30	0,32	0,92	0,5	0,44	0,23	0,3	0,50	0,17
9	24	14	1,08	1,3	1,56	1,38	0,70	0,50	1,00	1,25	1,1	1,22	0,85	0,7	0,67	0,83
10	9	20	0,17	0,8	0,22	0,31	0,10	0,31	0,17	0,50	0,5	0,78	0,69	0,4	0,67	1,17
11	3	23	0,08	0,5	0,67	0,08	0,10	0,56	0,67	1,75	1,3	0,78	1,08	1,2	2,68	0,50
12	14	22	0,33	0,3	0,67	0,31	0,20	0,34	0,50	0,92	0,4	0,56	0,15	0,4	0,50	0,33
13	6	22	0,22	0,3	0,44	0,15	0,10	0,32	0,32	0,42	0,8	0,565	0,54	0,4	0,60	0,50
14	32	13	1,08	1,0	1,22	1,00	0,40	0,19	0,67	0,08	0,3	0,66	0,16	0,1	0,50	0,35
15	14	27	1,00	1,0	1,22	0,77	0,70	0,83	1,83	0,83	0,7	0,89	0,85	0,6	1,33	1,00

где

X₁ – соматизация у мужчин;

X₂ – обессивность-импульсивность у мужчин;

X₃ – межличностная сензетивность у мужчин;

X₄ – депрессия у мужчин;

X₅ – тревожность у мужчин;

X₆ – враждебность у мужчин;

X₇ – паранойливые тенденции у мужчин;

X₈ – соматизация у женщин;

X₉ – обессивность-импульсивность у женщин;

X₁₀ – межличностная сензетивность у женщин;

X₁₁ – депрессия у женщин;

X₁₂ – тревожность у женщин;

X₁₃ – враждебность у женщин;

X₁₄ – паранойливые тенденции у женщин;

Y₁ – уровень стрессоустойчивости у мужчин;

Y₂ – уровень стрессоустойчивости у женщин.

Методические указания к задаче №8

Для установления вида зависимости требуется:

1) найти оценку уравнения регрессии вида

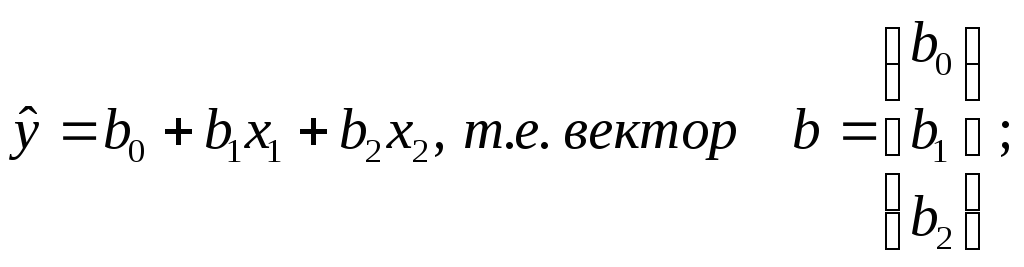
2) проверить значимость уравнения регрессии при =0,05 или=0,01;

3) проверить значимость отдельных коэффициентов регрессии

4) дать интерпретацию коэффициентам регрессии;

5) при необходимости перейти к алгоритму пошагового регрессионного анализа, отбросив один из незначимых коэффициентов регрессии;

6) построить матрицы парных и частных коэффициентов корреляции;

7) найти множественные коэффициенты корреляции и детерминации;

8) проверить значимость частных и множественных коэффициентов корреляции.

Задача 9. Имеются данные по 15 испытуемым, личности которых характеризуются тремя показателями (см. табл.): X₁ - уровень стрессоустойчивости; X₂ - враждебность; X₃ - паранойливые тенденции.

Таблица. Значения показателей личности испытуемых

	№	X1	X2	X3
Мужчины	1	12	0,55	0,33
	2	15	0,54	0,50
	3	9	0,59	0,17
	4	6	0,33	0,50
	5	20	0,38	1,17
	6	9	0,17	0,32
	7	17	0,33	1,33
Женщины	8	42	2,00	2,33
	9	37	1,33	1,00
	10	23	0,67	1,00
	11	20	0,67	1,17
	12	23	2,68	0,50
	13	22	0,50	0,33
	14	22	0,60	0,50
	15	27	1,33	1,00

В каждом варианте даны две обучающие выборки, первая из которых включает четверо мужчин (группа X), а вторая - пять женщин (группа Y).

Требуется:

1) найти оценки векторов средних и ковариационных матрицS_x, S_y;

2) определить несмещенную оценку суммарной ковариационной матрицы и обратной матрицы;

3) получить вектор оценок коэффициентов дискриминантной функции;

4) найти оценки значений дискриминантной функции U_x и U_y для матриц исходных данных Х и Y;

5) определить оценку константы C;

6) вычислить оценки значений дискриминантной функции для оставшихся испытуемых и провести их дискриминацию;

7) дать психологическую интерпретацию результатов дискриминации.