Формула бинома Ньютона
Выведем формулу, позволяющую возводить двучлен (бином) (а+b) в любую целую неотрицательную степень. Это формула бинома Ньютона. Она имеет следующий вид:
.
Докажем данную формулу методом математической индукции по n, где n≥0.
Формула верна при n = 0, 1, 2. В самом деле,
;
;
;
Пусть формула верна при n = k. Докажем ее при n = k + 1.
.
Раскрыв скобки и сгруппировав слагаемые по степеням а, получим:
.
С
учетом свойства 4 и того, что 
и
,
имеем:
Итак, индукция завершена, значит истинность формулы доказана.
В
формуле бинома Ньютона для (а + b)n
сумма степеней а
и b
в каждом слагаемом равна n.
Числа 
называются
биномиальными коэффициентами. При
вычислении биномиальных коэффициентов
удобно применять треугольник Паскаля.
В качестве примера найдем: а) (a + b)5; б) (х2-1)4:
а)
;
б)
Легко убедиться, что хорошо известные формулы сокращенного умножения для (a + b)2 и (a + b)3 представляют собой частные случаи формулы бинома Ньютона.
Упражнения
Докажите:
а)
;
б)
;
в)
.
Напишите разложение по формуле бинома Ньютона и упростите при необходимости:
а) (a + b)4; б) (a ― b)4; в) (a + 2b)5; г) (a – 2b)5;
д)
(1 + 2x)5;
е)
;
ж)
;
з)
;
и)
; к)
;
л)
; м)
;
н)
;
о)
;
п)
;
ж)
;
з)
;
и)
;
к)
;
л)
;
м)
;
Найдите:
а) шестой член разложения (1 ― 2z)21;
б)
шестой член разложения
;
в)
пятый
член разложения
;
г)
пятый
член разложения
;
д) два средних члена разложения (a3-ab)23;
е)
в разложении
член,
не содержащий x;
ж)
в разложении
член,
не содержащий z;
з)
в разложении
коэффициент
при а8;
и)
в разложении
коэффициент
при х4;
к) x, если третий член разложения (х +xlg x)5 равен 106 .
Самостоятельная работа по теме «Множества и элементы комбинаторики»
В конкурсе красоты участвуют 20 девушек. Сколько может быть вариантов распределения пяти призовых мест в этом конкурсе?
Сколькими способами 10 человек могут встать в очередь друг за другом?
Найти:
а)
шестой член разложения бинома 
;
б)
два средних члена разложения бинома 
.
Записать разложение бинома
.
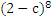В селении проживают 2000 жителей. Доказать, что по крайней мере двое имеют одинаковые инициалы.
Соответствия и отношения
Основные знания, умения и навыки, которыми должны овладеть студенты в процессе изучения этой темы:
понимать смысл неопределяемых понятий «соответствие», «отношение»;
знать свойства соответствий и отношений, уметь их определять и приводить конкретные примеры;
знать основные типы соответствий и отношений.
Основные понятия темы: соответствие, отношение.
Пусть даны два произвольных множества A и B.
О
п р е д е л е н и е 1. Декартовым
(прямым) произведением множеств
А и В называют множество, состоящее из
всех упорядоченных пар вида 
,
где 
и 
.
Символически это множество записывают так:
,
П р и м е р 1: Если А={1, 2, 3}, а В={0, 4}, то
;
.
Видим,
что в общем случае 
.
Пусть даны два произвольных множества X, Y.
Тройка
множеств 
,
где 
,
будем называть бинарным соответствием
между множеством X
и Y,
множество A
― его графиком, множество X
― областью отправления, Y
― областью прибытия.
Если
,
то говорят, что элемент x
находится
с элементом y
в
соответствии f
и пишут x
f
y,
то
есть 
.
З
а м е ч а н и е: Часто понятие бинарного
соответствия определяют как любое
подмножество А множества 
,
то есть отождествляют его с графиком
соответствия.
Множество
называют областью определения соответствия
f.
Множество
называют областью значения соответствия
f.
П
р и м е р 1. Пусть 
,
.
Тогда тройка множеств 
,
где 
и
будет
задавать соответствие между множествами
R
и R,
графиком которого будет парабола.
D(f)=R,
E(f)=R+.
.
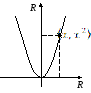
П
р и м е р 2: Пусть
,
.
.
,
.
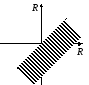
График
этого соответствия
представляет
собой полуплоскость.
A
Множество
называют полным
образом элемента
x
при соответствии f.
Множество
называют
полным
прообразом
элемента у
при соответствии f.
Из
определения 
и 
следует, что 
.
П р и м е р 3: Пусть X ― множество студентов в аудитории, У ― множество столов, за которым они сидят. Зададим соответствие х f у «студент x сидит за столом y». Тогда:
Областью отправления этого соответствия будет множество всех студентов в аудитории;
Областью определения ― множество студентов, которые сидят за столами;
Областью прибытия ― множество столов в аудитории.
Областью значений ― множество столов, за которыми сидит хотя бы один студент;
Графиком соответствия будет множество пар «студент- стол»
Полным прообразом студента х будет стол, за которым он сидит;
Полным прообразом стола у будут все студенты, которые за ним сидят.
П р и м е р 4:
Y
2
X a 5 4
с 1 b
3
Этот рисунок задает соответствие между множествами:
и
График
этого соответствия 
.
,
,
,
,
,
,
,
.
Из рассмотренных выше примеров видно, что соответствие может быть задано:
а)
путем
указания подмножества
(графически);
б)
аналитически;
х
f
у 
у
= f
(х);
в) с помощью графов или таблиц.
Графом называют множество точек, некоторые пары из которых соединены линиями с направлениями (см. пример 4).