Замечание

Правомочность использование булевских операций в данном алгоритме доказывается в целом ряде книг по диграфам.

Пусть [A(D)] – матрица смежности диграфаD=(V,E),n=|V|.

1. Пусть [Q₀]=[A(D)].

2. Сложить (булевская операция ) строку 1 матрицы [Q₀] к каждой строке [Q₀], которая имеет 1 в первом столбце. В результате получится матрица [Q₁]. Если первый столбец имеет только 0, тогда [Q₁]= [Q₀].

3. Сложить строку матрицы [Q₁] к каждой строке этой матрицы, которая имеет 1 во втором столбце. В результате получится матрица [Q₂]. Если втором столбце имеет только 0, тогда [Q₂]= [Q₃].

4. Для каждого j=3,…,nрассматривается матрица [Q_j-1]. Сложить строкуjк каждой строке матрицы [Q_j-1], у которойj-ый столбец имеет 1. В результате получится матрица [Q_j]. Еслиj-ый столбец имеет только 0, тогда [Q_j]= [Q_j-1].

5. Записать [R(D)]=[Q_n].

С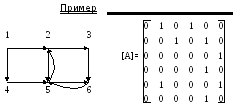ложность алгоритма –O(n³).

• [Q₀]=[A(D)].

• Первая строка [Q₀] не имеет 1 в первом столбце. Поэтому [Q₁]=[Q₀].

• Строка 2 суммируется со строками 1 и 5 (имеют 1 во втором столбце):

• Строка 3 суммируется со строками 1,2 и 5:

• Сложить строку 4 со строкой 1. Результат – [Q₃]=[Q₄].

• Сложить строку 5 со строками 1,2,4,5 и 6:

• Сложить строку 6 со всеми строками:

3.8. Направленные деревья

Диграф D(V,E) называетсянаправленным деревом,если он имееткорень rи еслиrVи каждая вершинадостижима из вершиныr, т.е. имеются дипути, которые начинаются наrи заканчиваются на каждой вершинеv.

Существуют несколько эквивалентных определений направленного дерева.

Пусть D= (V,E) будет диграфом. Тогда следующие определения эквивалентны:

• Dявляется направленным деревом.

• Dимеет корень, из которого имеется уникальный дипуть к каждой вершине.

• Dимеет кореньr, для которогоdeg⁺(r)=0, а для всех других вершинvdeg⁺(v)=1.

• Dимеет корень, но удаление дуги (но не вершины) нарушает это условие.

• Неограф основания диграфа Dявляется связным иDимеет одну вершинуr, для которойdeg⁺(r)=0, а для остальных вершинvdeg⁺(v)=1.

Вершины направленного дерева v, имеющиеdeg^–(v)=0, являются еголистьями. Направленныйлессостоит из направленных деревьев.

Поддиграф Hконечного диграфаDназываетсянаправленным каркасным деревом, если поддиграф Н является направленным деревом, содержащим все вершиныD.

Число направленных каркасных деревьев с корнем rдиграфа задается минором его матрицы ЛапласаL⁺, который вычисляется при удаленииr-ых строки и столбца.

3.10. Топологическое упорядочение

Направленным ациклическим графом(directedacyclicdraph–DAG) является диграф без направленных циклов.

Алгоритм основан на обходе в глубину (DFS) и базируется на следующем утверждении:

• диграф будет ациклическим тогда и только тогда, когда обход в глубину не содержит обратных дуг.

В общем случае под топологическим упорядочением вершин диграфапонимается такое разбиение его вершин на группы (ранги, слои), при котором:

1. вершины первой группы не имеют предшествующих вершин, а вершины последней группы – последующих;

2. вершины любой другой группы не имеют предшествующих в следующей группе;

3. вершины одной и той же группы дугами не соединены.

В результате топологического упорядочения вершин диграфа получается диграф, изоморфный данному. Этот диграф называется диграфом зависимостей.

Топологическое упорядочение вершин позволяет выявить причинно-следственные связи диграфа.

Диграф имеет топологическое упорядочение тогда и только тогда, когда он является ациклическим (DAG).

Проблема топологического упорядочения вершин диграфа решается за линейное время.

Обход в глубину позволяет решать две проблемы:

• определить, имеются ли циклы в диграфе. Если циклы имеются, алгоритм останавливается после их обнаружения. В случае ацикличности диграфа DFSопределяет времена завершенияf[n] обхода вершин.

• Топологическое упорядочение вершин задается списком времен обнаружения, записанном в порядке уменьшения.

Сложность алгоритма – О(n+m),n=|V|,m=|E|.

Алгоритм Фалкерсона позволяет построить топологическое упорядочение ациклического диграфа (DAG) вместе с разбиением вершин на группы (ранги, слои). Существует две разновидности алгоритма: графическая и матричная.

Графический вариант алгоритма Фалкерсона:

1. Найти вершины диграфа, в которые не входит ни одна дуга. Эти вершины образуют первую группу. Обозначим вершины первой группы v_i^I. Поместить эти вершины на вертикаль первой группы.

2. Мысленно вычеркнуть все пронумерованные вершины и дуги, из них выходящие. В получившемся диграфе найдется по крайней мере одна вершина, в которую не входит ни одна дуга. Этой вершине, входящей во вторую группу, присвоить номера v_i^II, поместить их на вертикаль второй группы и соединить дугами вершины первой и второй вертикали.

3. Повторить шаг 2 для следующих групп до тех пор, пока все вершины не будут пронумерованы, помещены на соответствующие вертикали и не соединены дугами. В результате будет построен диграф зависимостей.

Пример

Шаг 1.

Ввершину Х₆не входи ни одна дуга. Х₆входит в первую группу вершин. Мысленно вычеркиваемые линии диграфа обозначены пунктирными линиями.

Шаг 2.

Ввершины не входит ни одна дуга. Вершины Х₂и Х₄входят во вторую группу. Обозначим эти вершины Х₂^IIи Х₄^IIи поместим их на вертикальIIгруппы. Соединяем в диграфе зависимостей вершиныIиIIгрупп соответствующими дугами. Мысленно отбрасываемые дуги помечаем в исходном диграфе пунктирными линиями.

Шаг 3.

В вершины Х₃и Х₅не входит ни одна дуга. Вершины Х₃и Х₅образуютIIIгруппу. Помечаем эти вершины как Х₃^IIIи Х₅^IIIи помещаем их на третью вертикаль диграфа зависимостей. Мысленно отбрасываемые дуги в исходном диграфе помечаем штриховыми линиями.

Шаг 4.

В вершину Х₁не входит ни одна дуга. Вершина Х₁входит вIVгруппу. Обозначим эту вершину Х₁^IVи поместим ее на четвертую вертикаль. Соединяем вершиныI,II,IIIиIVгрупп соответствующими дугами. Мысленно отбрасываемую дугу помечаем штриховой линией. Непомеченной остается только вершина Х₇.

Шаг 5.

Оставшаяся вершина Х₇входит вVгруппу. Обозначим эту вершину Х₇^Vи поместим ее на пятую вертикаль. Соединяем вершиныI,II,II,IVиVгрупп соответствующими дугами. В результате получается полный диграф зависимостей исходного диграфа.