
- •Высшая математика
- •Тема 1. Кратные интегралы.
- •1.2 Вычисление двойного интеграла в декартовых координатах
- •1.3 Вычисление двойного интеграла в полярных координатах
- •1.4 Приложения двойного интеграла
- •1.5 Тройной интеграл
- •1.6 Вычисление тройного интеграла в декартовых координатах
- •1.7 Замена переменных в тройном интеграле.
- •1.8 Геометрические и физические приложения тройных интегралов
- •2. Криволинейные интегралы
- •2.1 Криволинейные интегралы второго рода. Основные понятия
- •2.2Вычисление криволинейных интегралов второго рода
- •2.3 Формула Остроградского – Грина.
- •2.4 Условия независимости криволинейного интеграла II рода от пути интегрирования
- •2.5 Некоторые приложения криволинейного интеграла II рода
- •3. Элементы теории поля
- •3.1 Скалярное поле
- •3.2 Векторное поле
- •3.3 Специальные виды векторных полей
- •3.4 Оператор Гамильтона. Векторные дифференциальные операции
- •4. Числовые и степенные ряды
- •4.1 Числовые ряды. Основные понятия.
- •4.2 Признаки сходимости числовых рядов
- •4.3 Знакочередующиеся ряды и знакопеременные ряды
- •4.4 Степенные ряды
- •4.5 Ряды Тейлора и Маклорена
- •4.6 Разложение некоторых элементарных функций в ряд Маклорена
- •4.7 Некоторые приложения степенных рядов
- •5. Ряды фурье
- •5.1 Периодические функции и процессы
- •5.2 Тригонометрический ряд Фурье
- •5.3 Разложение в ряд Фурье четных и нечетных функций
- •5.4 Разложение в ряд Фурье функций произвольного периода
- •5.5 Представление непериодической функции рядом Фурье
- •6. Элементы операционного исчисления
- •6.1 Оригиналы и их изображение
- •6.2 Свойства преобразований Лапласа
- •6.3 Отыскание оригиналов по изображениям
- •6.4 Операционный метод решения линейных дифференциальных уравнений и их систем
- •98309 Г. Керчь, Орджоникидзе, 82
4. Числовые и степенные ряды
4.1 Числовые ряды. Основные понятия.
Определение 1.
Пусть задана бесконечная последовательность
чисел
![]()
Выражение
![]() называется числовым
рядом. (4.1.1)
называется числовым
рядом. (4.1.1)
При
этом
![]() - называются членами ряда,
- называются членами ряда,![]() - общий член ряда.
- общий член ряда.
Ряд (4.1.1) считается
заданным, если известен общий член ряда
![]() ,
выраженный, как
функция его номера n:
,
выраженный, как
функция его номера n:![]() .
Обычноn полагают
равным1,2,3,…,иногда начинают ряд сn=0.
.
Обычноn полагают
равным1,2,3,…,иногда начинают ряд сn=0.
Определение 2.
Сумма конечного числа первых n
членов ряда называетсячастичной
суммойряда и обозначается через![]() ,
т.е.
,
т.е.![]() .
.
Примеры частичных сумм:
![]()
Определение 3. Если
частичная сумма
![]() ряда (4.1.1) имеет при
ряда (4.1.1) имеет при![]() конечный пределS,то данный ряд называютсходящимся,
а числоS– называют
суммой ряда.
конечный пределS,то данный ряд называютсходящимся,
а числоS– называют
суммой ряда.
![]()
Если же частичная
сумма
![]() не имеет конечного придела, то говорят,
что данный ряд расходиться и ряд называютрасходящимся.(
не имеет конечного придела, то говорят,
что данный ряд расходиться и ряд называютрасходящимся.(![]() или
или![]() - не существует.)
- не существует.)
Примеры: 1) Ряд
![]() нельзя считать заданным, а ряд 2+5+8+… -
можно,
нельзя считать заданным, а ряд 2+5+8+… -
можно,![]() .
.
2) Ряд 0+0+0+… сходится, S=0 (сумма равна нулю);
3) Ряд
1+1+1+1+… расходится,
![]()
![]() ;
;
4) Ряд 1-1+1-1+1-1+…
расходится, так как частичные суммы
![]() и
и![]() - не имеет предела.
- не имеет предела.
5) Ряд
![]() сходится. Имеем
сходится. Имеем![]() .
Запишем первыеn
членов рада
.
Запишем первыеn
членов рада
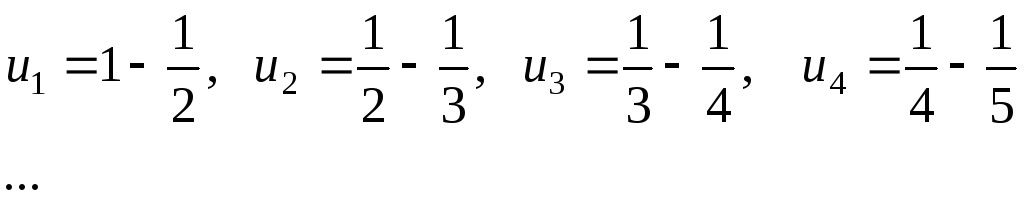
![]() .
.
Складывая их
получаем
![]() ,
находим
,
находим![]() .
Таким образом, ряд сходится и его сумма
равна 1.
.
Таким образом, ряд сходится и его сумма
равна 1.
Свойства рядов.
Е
 сли
ряд
сли
ряд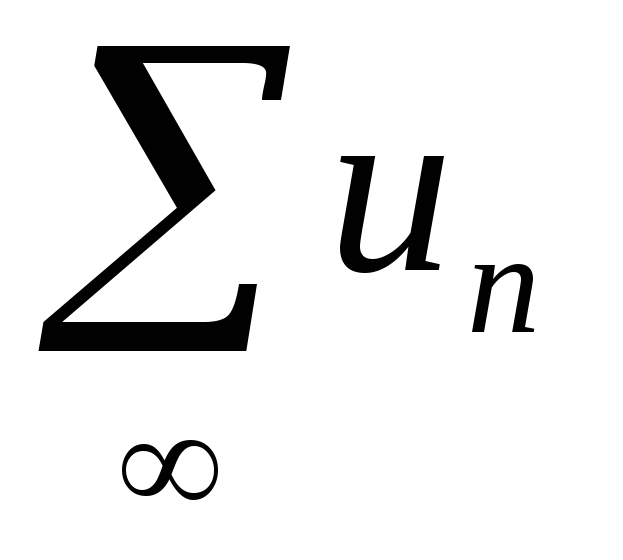 сходится
и его сумма равнаS,
то ряд
сходится
и его сумма равнаS,
то ряд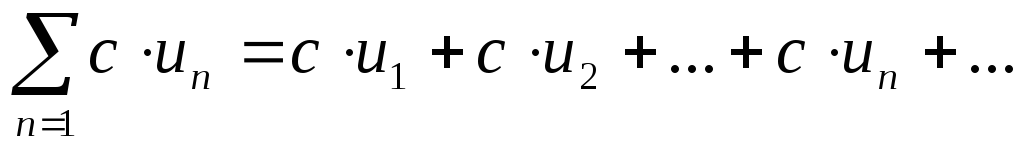 ,
(4.1.2)
,
(4.1.2)
где с– произвольное число, так же сходится и его сумма ранас∙S,т.е. ряд можно почленно умножать на одно и то же число.
Если же ряд
![]() - расходиться ис не равно нулю, то
и ряд (4.1.2) расходится.
- расходиться ис не равно нулю, то
и ряд (4.1.2) расходится.
Два сходящихся ряда
 и
и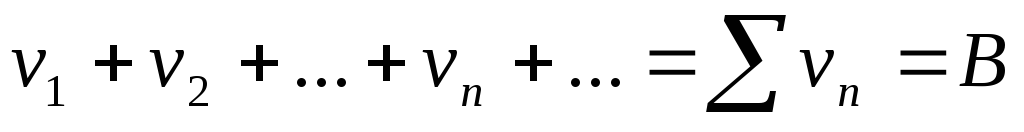 можно почленно складывать и вычитать,
причем полученные ряды
можно почленно складывать и вычитать,
причем полученные ряды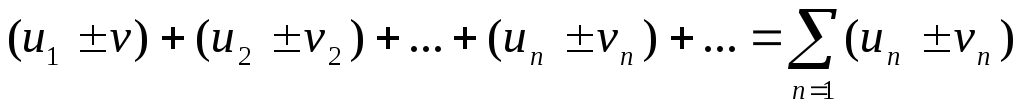 так же сходятся, имея своей суммой
соответственно
так же сходятся, имея своей суммой
соответственно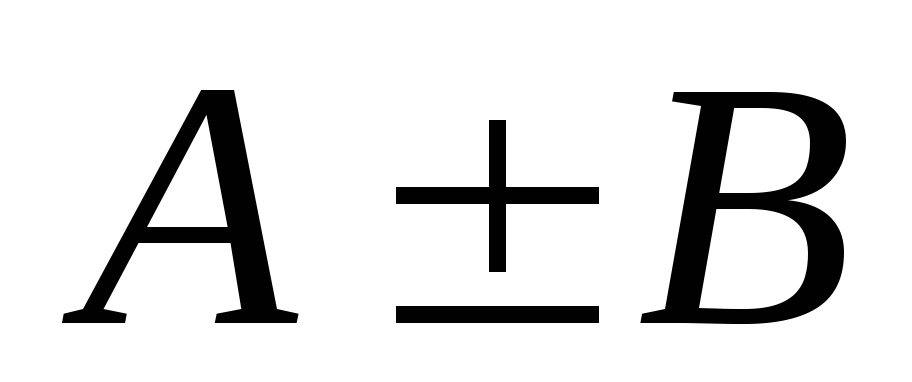
Замечание: из свойства 2 вытекает, что сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд.
Сумма (разность) двух расходящихся рядов может быть как сходящимся рядом, так и расходящимся.
3. Если к ряду
![]() прибавить (или отбросить) конечное число
членов ряда, то полученный ряд и исходный
ряд сходятся или расходятся одновременно.
прибавить (или отбросить) конечное число
членов ряда, то полученный ряд и исходный
ряд сходятся или расходятся одновременно.
Исходный ряд -
![]() ,
(*)
,
(*)
новый ряд, получен отбрасыванием первых nчленов ряда
![]() (**)
(**)
Если ряд (*) сходится, то ряд (**) также сходится, если ряд (*) расходится, то ряд (**) также расходится.
Замечание к 3 свойству.
Ряд
![]() называютп-м остатком ряда
называютп-м остатком ряда
он получается из
ряда (4.1.1) отбрасыванием первых nчленов. И если ряд (4.1.1) сходится, т.е.![]() то его остаток
то его остаток![]() стремится к нулю при
стремится к нулю при![]() ,т.е.
,т.е.![]() .
.
Арифметическая, геометрическая прогрессии. Ряд геометрической прогрессии
Арифметическая прогрессия- последовательность чисел, в которой разность между последующим и предыдущим членами остается неизменной.
![]()
![]()
d
– разность арифметической прогрессии.
Если известен первый член![]() и разность прогрессииd,
то
и разность прогрессииd,
то![]() .
.
Пример: 1) 2,5,8,11
![]()
2) 5,3,1,-1,-3
![]()
Геометрическая прогрессия- последовательность чисел, в которой отношение последующего члена к предыдущему есть величина постоянная.
![]()
![]() ,
,
![]() -знаменатель
прогрессии.
-знаменатель
прогрессии.
![]() - формула n-го
члена геометрической прогрессии, если
известен первый член
- формула n-го
члена геометрической прогрессии, если
известен первый член![]() и знаменательq.
и знаменательq.
Пример: 2,4,8,16…
![]() ,
,![]()
3,6,12,24…
![]() ,
,![]()
Определение.
Ряд
![]()
![]() (4.1.3) называетсярядом
геометрической прогрессии.
(4.1.3) называетсярядом
геометрической прогрессии.
Исследуем ряд
(4.1.3) на сходимость. Сумма первых n-членов
геометрической прогрессии находится
по формуле![]() .
.
Найдем предел этой суммы
![]()
Рассмотрим случаи:
Если
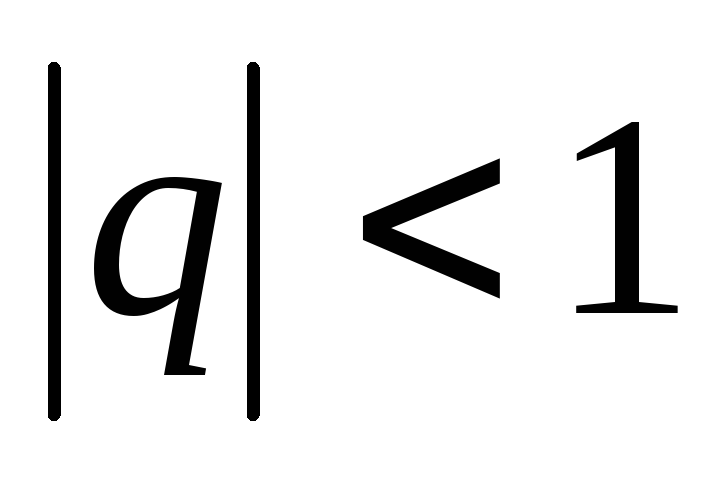 ,
то
,
то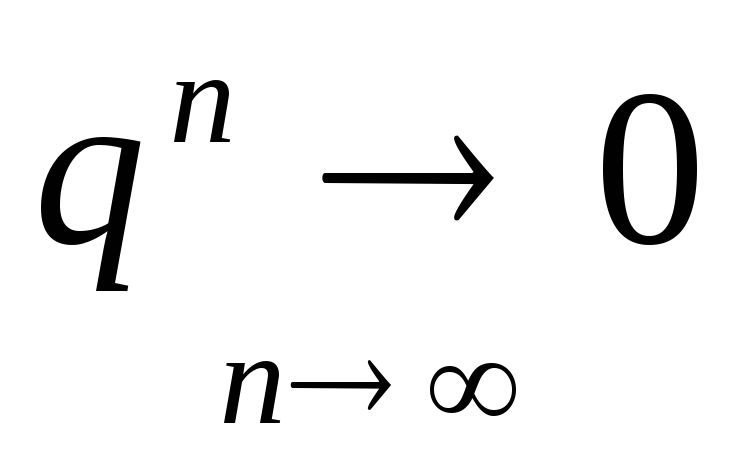 ,
поэтому
,
поэтому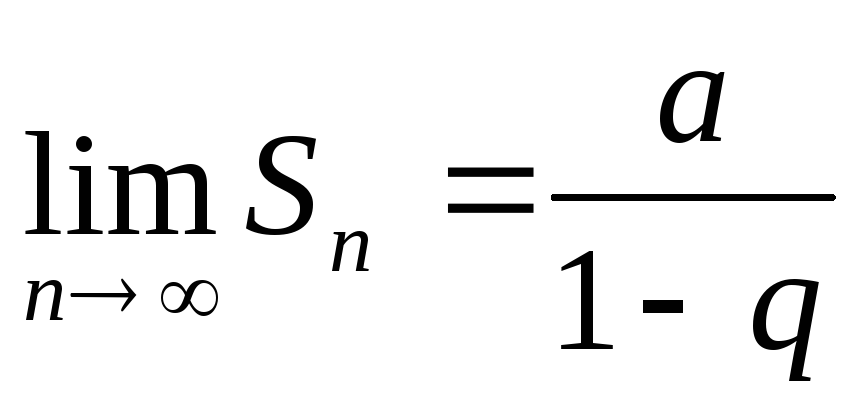 следовательно, если
следовательно, если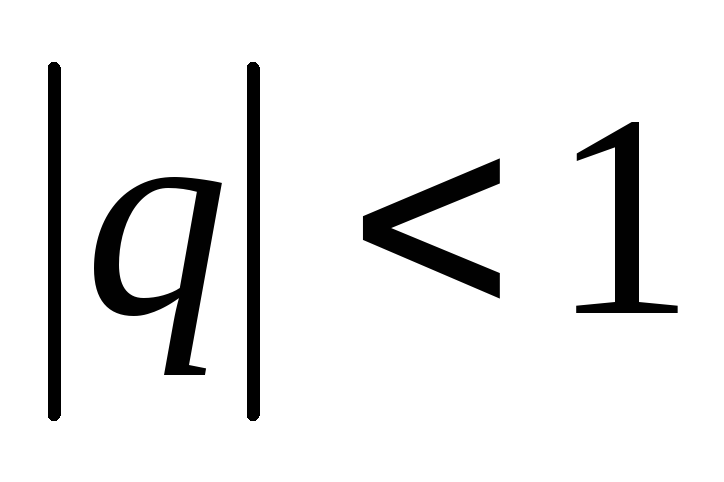 ,
ряд сходится.
,
ряд сходится.
Если
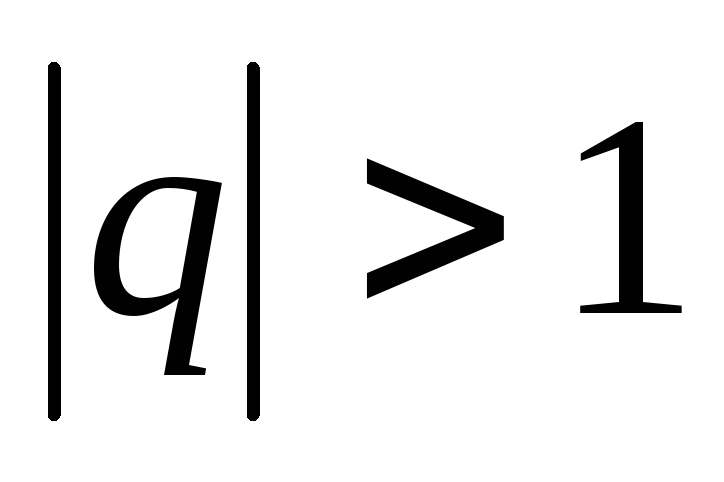 , то
, то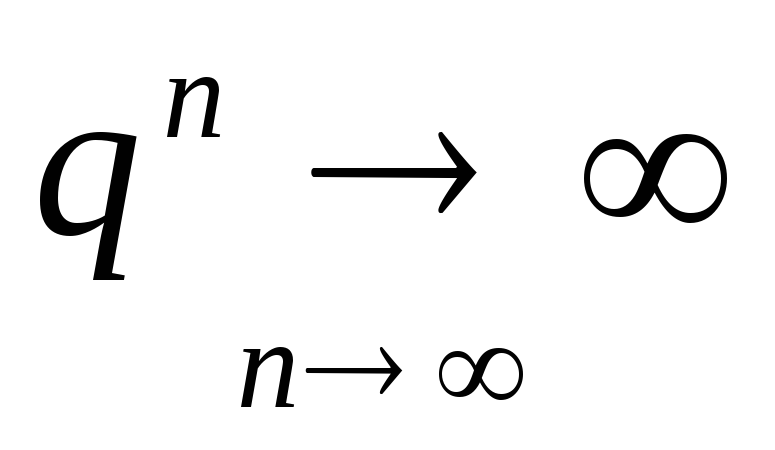 ,
,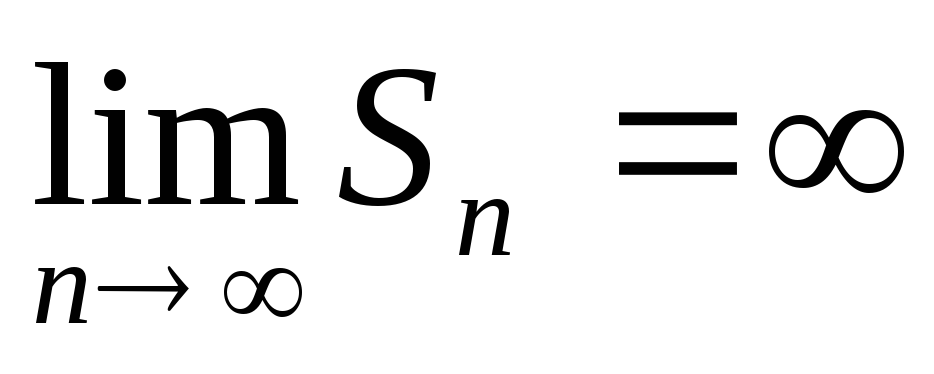 ,
ряд расходится.
,
ряд расходится.
Если
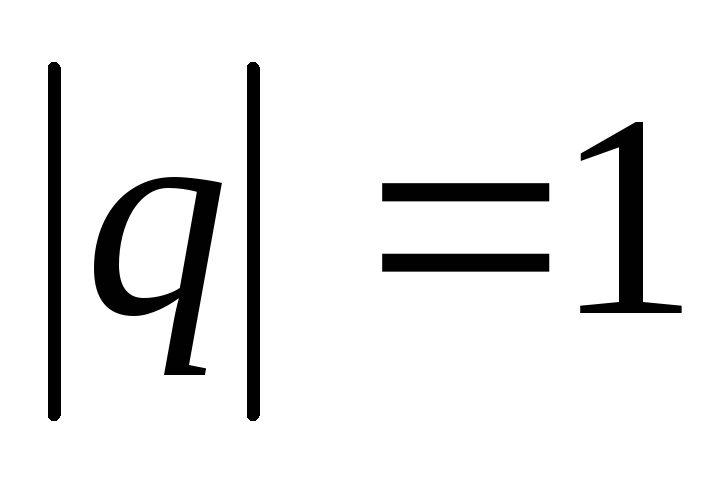 ,
то приq=1ряд
примет вид
,
то приq=1ряд
примет вид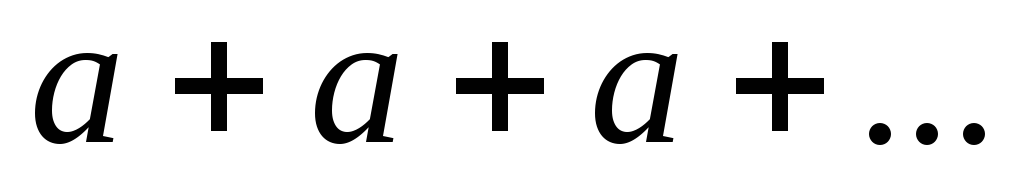 .
Тогда
.
Тогда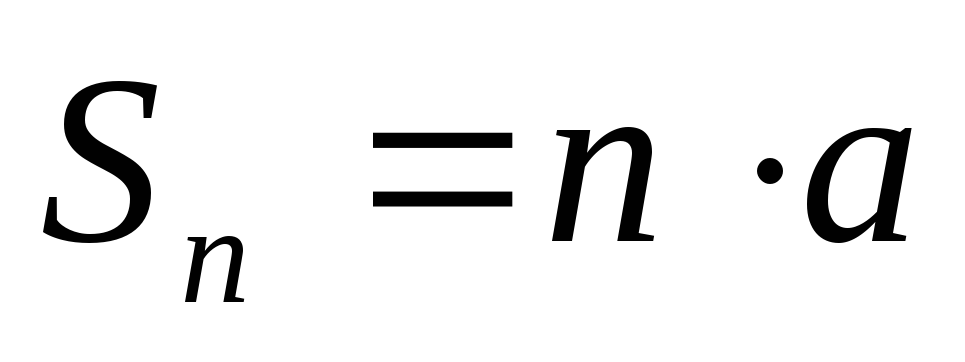
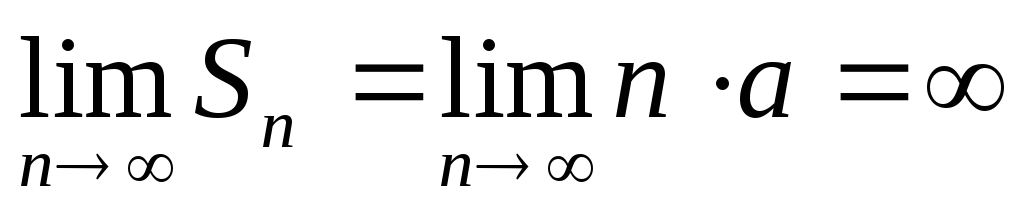 .
При q=
-1ряд принимает вид
.
При q=
-1ряд принимает вид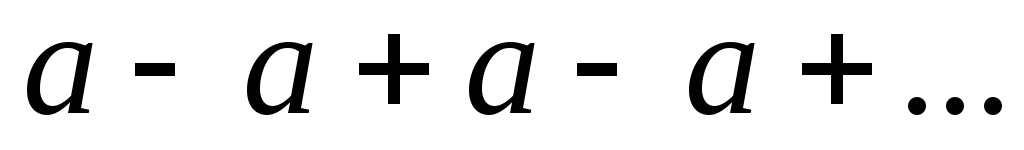 и
и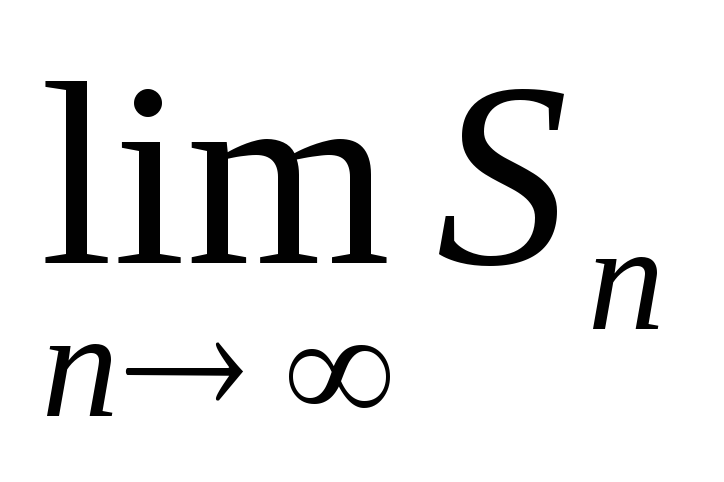 - не существует.
- не существует.
Следовательно ряд
при
![]() расходится.
расходится.
Итак ряд геометрической
прогрессии сходится при
![]() и расходится при
и расходится при![]() .
.
Примеры:
![]() расходится
расходится![]() .
.
![]() сходится
сходится
![]() .
.
