4. Теоретические и эмпирические частоты. Критерии согласия.

Эмпирические частоты - частоты, полученные в результате опыта (наблюдения). Теоретические частоты расcчитываются по формулам. Для нормального закона распределения их можно найти следующим образом:

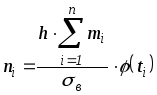, (11.3)

где - сумма эмпирических частот, - разность между двумя соседними вариантами, - выборочное среднеквадратическое отклонение, , - выборочная средняя арифметическая.

Обычно эмпирические и теоретические частоты различаются. Возможно, что расхождение случайно и связано с ограниченным число наблюдений; возможно, что расхождение неслучайно и объясняется тем, что для вычисления теоретических частот выдвинута статистическая гипотеза о том, что генеральная совокупность распределена нормально, а в действительности это не так. Распределение генеральной совокупности, которое она имеет в силу выдвинутой гипотезы, будем называть теоретическим.

Возникает необходимость установить правило (критерий), которое позволяло бы судить, является ли расхождение между эмпирическим и теоретическим распределениями случайным или значимым. Если расходжение окажется случайным, то можно считать, что данные наблюдений (выборки) согласуются с выдвинутой гипотезой о законе распределения генеральной совокупности и, следовательно, гипотезу можно принять; если же расхождение окажется значимым, то данные наблюдений не согласуются с гипотезой, и ее следует отвергнуть.

Критерием согласия называют критерий, который позволяет установить, является ли расхождение эмпирического и теоретического распределений случайным или значимым, т. е. согласуются ли данные наблюдений с выдвинутой статистической гипотезой или не согласуются.

Имеется несколько критериев согласия: критерий (Пирсона), критерий Колмогорова, критерий Романовского и др. Ограничимся описанием того, как применяется критерий к проверке гипотезы о нормальной распределении генеральной совокупности (критерий применяется аналогично и для других распределений).

Допустим, что в результате наблюдений получена выборка:

значение признака . . .

эмпирическая частота . . .

Выдвинем статистическую гипотезу: генеральная совокупность, из которой извлечена данная выборка, имеет нормальное распределение. Требуется установить, согласуется ли эмпирическое распределение с этой гипотезой. Предположим, что по формуле (11.3) вычислены теоретические частоты , , ... , . Обозначим через среднее арифметическое квадратов разностей между эмпирическими и теоретическими частотами, взвешенное по обратным величинам теоретических частот

.

Чем больше согласуются эмпирическое и теоретическое распределения, тем меньше будут различаться эмпирические и теоретические частоты, тем меньше будет . Отсюда следует, что характеризует близость эмпирического и теоретического распределений. Очевидно, в разных опытах будет принимать различные, наперед неизвестные значения, т. е. является случайной величиной. Плотность вероятности этого распределения (для выборки достаточно большого объема) не зависит от проверяемого закона распределения, а зависит от параметра , называемого числом степеней свободы. При проверке гипотезы о нормальном распределении генеральной совокупности , где - число групп, на которые разбиты данные наблюдений. Имеются таблицы (приложение 6), в которых указана вероятность того, что в результате влияния случайных факторов величина примет значение, не меньшее чем вычисленное по данным выборки .

Примем для определенности уровень значимости . Если вероятность найденная по таблицам, окажется меньше, чем , то это означает, что в результате влияния случайных причин наступило событие, которое практически невозможно. Таким образом, тот факт, что приняло значение , нельзя объяснить случайными причинами; его можно объяснить тем, что генеральная совокупность не распределена нормально, и значит, выдвинутая гипотеза о нормальном распределении генеральной совокупности, не согласующаяся с данными наблюдений, должна быть отвергнута. Аналогичными рассуждениями можно прийти к заключению, что если вероятность, найденная по таблицам, больше , то гипотеза о нормальном распределении генеральной совокупности согласуется с данными наблюдений и поэтому может быть принята. Полученные выводы распространяются и на другие уровни значимости.

На практике надо следить за тем, чтобы объем выборки был достаточно велик () и чтобы каждая группа содержала не менее 5 - 8 значений признака.

Для проверки гипотезы о нормальном распределении генеральной совокупности нужно:

1) вычислить теоретические частоты по формуле (11.3);

2) вычислить , где - эмпирические частоты, а - теоретические частоты;

3) вычислить число степеней свободы , где - число групп, на которые разбита выборка;

4) выбрать уровень значимости;

5) найти по таблице (см. приложение 6) по найденным и вероятность , причем если эта вероятность меньше принятого уровня значимости, то гипотезу о нормальном распределении генеральной совокупности отвергают; если вероятность больше уровня значимости, то гипотезу принимают.

Пример 5. Проверить, согласуются ли данные выборки со статистической гипотезой о нормальном распределении генеральной совокупности, из которой извлечена эта выборка:

варианта 15 20 25 30 35 40 45 50 55

частота 6 13 38 74 106 85 30 10 4

Решение. Вычислим выборочное среднее и выборочную дисперсию по формулам п.1: , . Вычислим теоретические частоты по формуле (11.3):

15 20 25 30 35 40 45 50 55	6 13 38 74 106 85 30 10 4	-19,7 -14,7 -9,7 -4,7 0,3 5,3 10,3 15,3 20,3	-2,67 -1,99 -1,31 -0,63 0,05 0,73 1,41 2,09 2,77	0,0113 0,0551 0,1691 0,3271 0,3984 0,3056 0,1476 0,0449 0,0086	3 14 42 82 99 76 37 11 2
					=366

Найдем . Вычислим число степеней свободы учитывaя, что число групп выборки : . Примем уровень значимости равным . По таблице (см. приложение 6) при и находим вероятность ; при вероятность . Пользуясь линейной интерполяцией, получим приближенное значение искомой вероятности, равное . Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.