
- •Вища математика
- •Тематичні індивідуальні завдання та приклади розв’язання типових завдань з курсу „Вища математика”
- •Харків 2009
- •Передмова
- •§1. Елементи лінійної алгебри Завдання 1. В задачах варіантів 125 обчислити визначник четвертого порядку
- •Завдання 2.
- •Розв’язання типового варіанта.
- •Якщо матриця а є невиродженою, то
- •§2. Елементи векторної алгебри Завдання 3.
- •Розв’язання типового варіанта.
- •§3. Аналітична геометрія
- •Розв’язання типового варіанта
- •4. Дано координати точок: а (–1; 4; 2); в(0; 3; 3); с(4; –5; 3) і м(1; –3; 5).
- •§4. Вступ до математичного аналізу
- •Розв’язання типового варіанта.
- •2.Знайти границі:
- •3. Знайти границю
- •§5. Диференціальне числення функції однієї змінної
- •Розв’язання типового варіанта
- •1.Знайти похідні функцій:
- •§6. Функції багатьох змінних
- •§7. Інтегральне числення функції однієї змінної
- •Розв’язання типового варіанта
- •§8. Диференціальні рівняння
- •Розв’язання типового варіанта.
- •Дане рівняння приймає вигляд
- •Відповідне однорідне рівняння
- •Підставляючи , ,в дане рівняння, маємо
- •Розв’язуючи систему, знаходимо
- •§9. Ряди
- •Розв’язання типового варіанта
- •§10. Теорія ймовірностей та математичної статистики
- •Вихідні дані до задач
- •Список літератури
- •Вища математика
- •Тематичні індивідуальні завдання та приклади розв’язання типових завдань з курсу „Вища математика”
- •Харківський державний університет харчування та торгівлі.
Розв’язання типового варіанта
1.
Задано трикутник з координатами вершин
А(–2;
4); В(6;
–2); С(8;
7). Необхідно знайти: 1) довжину сторони
АВ; 2)
рівняння сторін АВ
і АС та
їх кутові коефіцієнти; 3) рівняння медіан,
що проведені з вершин А
і В,
координати центру ваги трикутника; 4)
величину кута А
в радіанах з точністю до двох знаків;
5) рівняння висоти СТ,
проведеної з вершини С
на сторону АВ;
6) координати точки М,
розташованої симетрично точці В
відносно до прямої СТ;
7) Побудувати трикутник АВС
медіани, висоту в системі координат
![]() .
Зробити малюнок.
.
Зробити малюнок.
►1) Відстань між точками A(x1,y1) і B(x2,y2) площини визначається за формулою:
![]() (11.1)
(11.1)
Застосовуючи (11.1), знаходимо довжину сторони АВ:
![]() .
.
2) Рівняння прямої, що проходить через точки A(x1, y1) i B(x2, y2), має вигляд
![]() .
(11.2)
.
(11.2)
Щоб скласти рівняння сторони АВ, підставляємо в (11.2) координати точок А і В:
![]()
![]()
![]() 4y
– 16 = –3x
– 6;
4y
– 16 = –3x
– 6;
3x + 4y – 10= 0 (AB).
Для знаходження кутового коефіцієнта прямої АВ (КАВ), розв’я-жемо отримане рівняння відносно у:
4y =
–3x +
10; y =
![]() .
.
Отже,
KAB=
![]() .
.
Підставляючи в (11.2) координати точок А і С, здобуваємо рівняння прямої АС:
![]()
![]()
10y – 40 = 3x + 6; 3x – 10y + 46 = 0 (AC),
звідки кутовий коефіцієнт
KAC
=
![]() .
.
Нехай точка D – середина відрізку ВС, а точка Е – середина
відрізку АС.
Для визначення координат точок D і Е застосовуємо формули:
![]() ;
y
=
;
y
=
![]() ;
;
xD=
![]() ;yD=
;yD=
![]() ,D
,D
![]() ,
,
xE=
![]()
![]() ;yE=
;yE=![]() ,E
,E
![]() .
.
Підставляючи координати точок А і D в (11.2), маємо рівняння медіани АD:
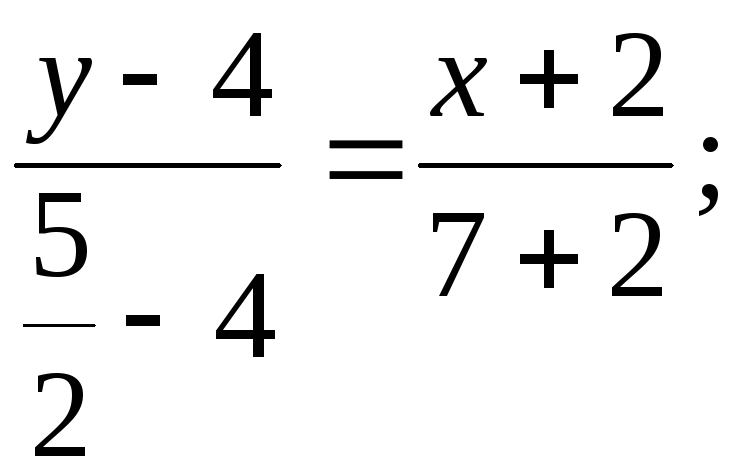
![]()
![]()
6y – 24 = x – 2; x + 6y – 22 = 0 (AD).
Аналогічно знаходимо рівняння медіани ВЕ:
5x + 2y – 26 = 0 (BE).
Центр ваги трикутника знаходиться в точці N перетину його медіан. Щоб знайти координати цієї точки, необхідно розв’язати систему рівнянь прямих АD і ВЕ.
Унаслідок розв’язку системи
![]()
маємо х = 4, у = 3.
Отже, N (4; 3) – точка перетину медіан.
Крім того, відомо, що точка перетину медіан ділить кожну медіану у відношенні 2:1 (починаючи з вершини), тобто
![]() .
.
Тому координати точки N можна знайти також, застосовуючи формули ділення відрізку в даному відношенні:
x=![]()
![]() .
(11.3)
.
(11.3)
Підставляючи в (11.3) координати точок В і Е та вважаючи =2, маємо:
![]()
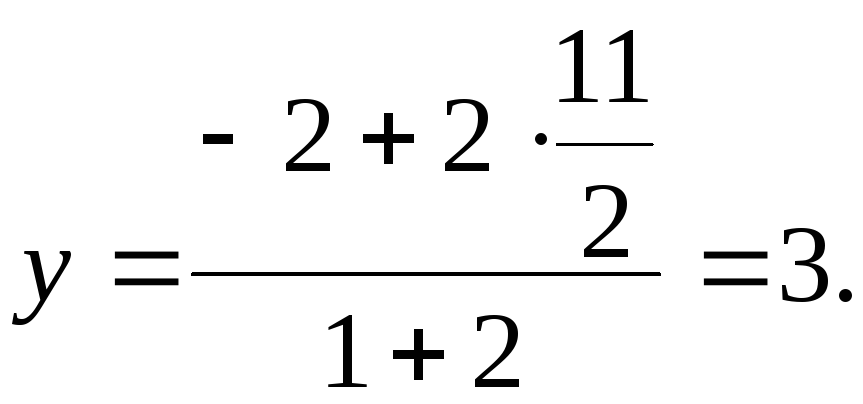
3) Гострий кут між прямими, кутові коефіцієнти яких, відпо-відно, дорівнюють К1 та К2, можна знайти за формулою
![]() .
(11.4)
.
(11.4)
Шуканий кут А утворюється прямими АВ і АС, кутові коефі-цієнти яких знайдено раніше. Отже, застосовуючи формулу (11.4), маємо:
tgA=![]() =
=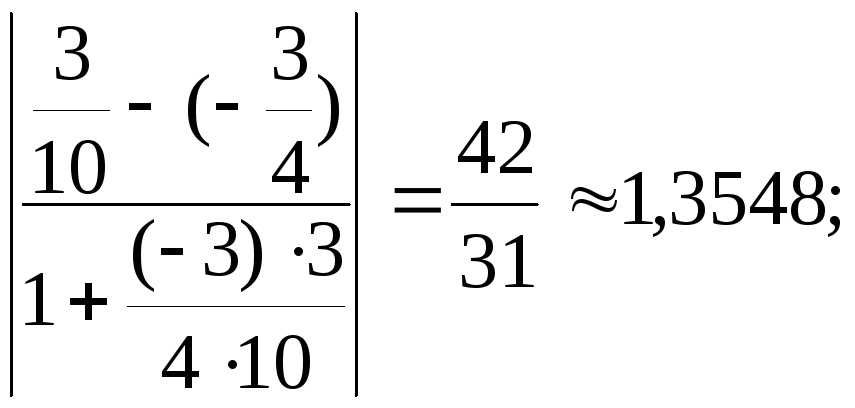
A = arctg 1,354853,480.
Скориставшись таблицями переведення градусної міри в радіанну, знаходимо
A 0,935 рад.
Рівняння прямої, що проходить через дану точку в даному напрямку, має вигляд
y – y1=K(x– x1). (11.5)
Для знаходження кутового
коефіцієнта висоти СТ
скористаємось умовою перпендикулярності
прямих СТ
і АВ:
![]() =
–1. Оскільки
=
–1. Оскільки![]() ,
то
,
то![]()
Підставляючи в (11.5) координати точки С, а також значення знайденого кутового коефіцієнта висоти СТ, маємо:
![]() ;
3y –
21 = 4x –
32; 4x –3
y – 11 =
0 (CT).
;
3y –
21 = 4x –
32; 4x –3
y – 11 =
0 (CT).
Пряма АВ перпендикулярна до прямої СТ, а шукана точка М, симетрична точці В (2; –2) відносно до прямої СТ, належить прямій АВ. Крім того, точка Т є серединою відрізку МВ. Визначимо координати точки Т. Для цього розв’яжемо систему рівнянь, яку утворюють рівняння прямих АВ і СТ.
![]()
6) Враховуючи, що точка Т (2,96; 0,28) – середина відрізку МВ, а також користуючись формулами (11.3), знайдемо координати точки М:
2,96 =
![]() ХM
= 0,28;
ХM
= 0,28;
0,28 =
![]() YM
= 2,56.
YM
= 2,56.
7) Трикутник АВС,
медіани АD
і ВЕ,
точку N
їх перетину, висоту СТ,
що побудовані в системі координат
![]() ,
подано на рис. 1.
,
подано на рис. 1.
![]()
![]()
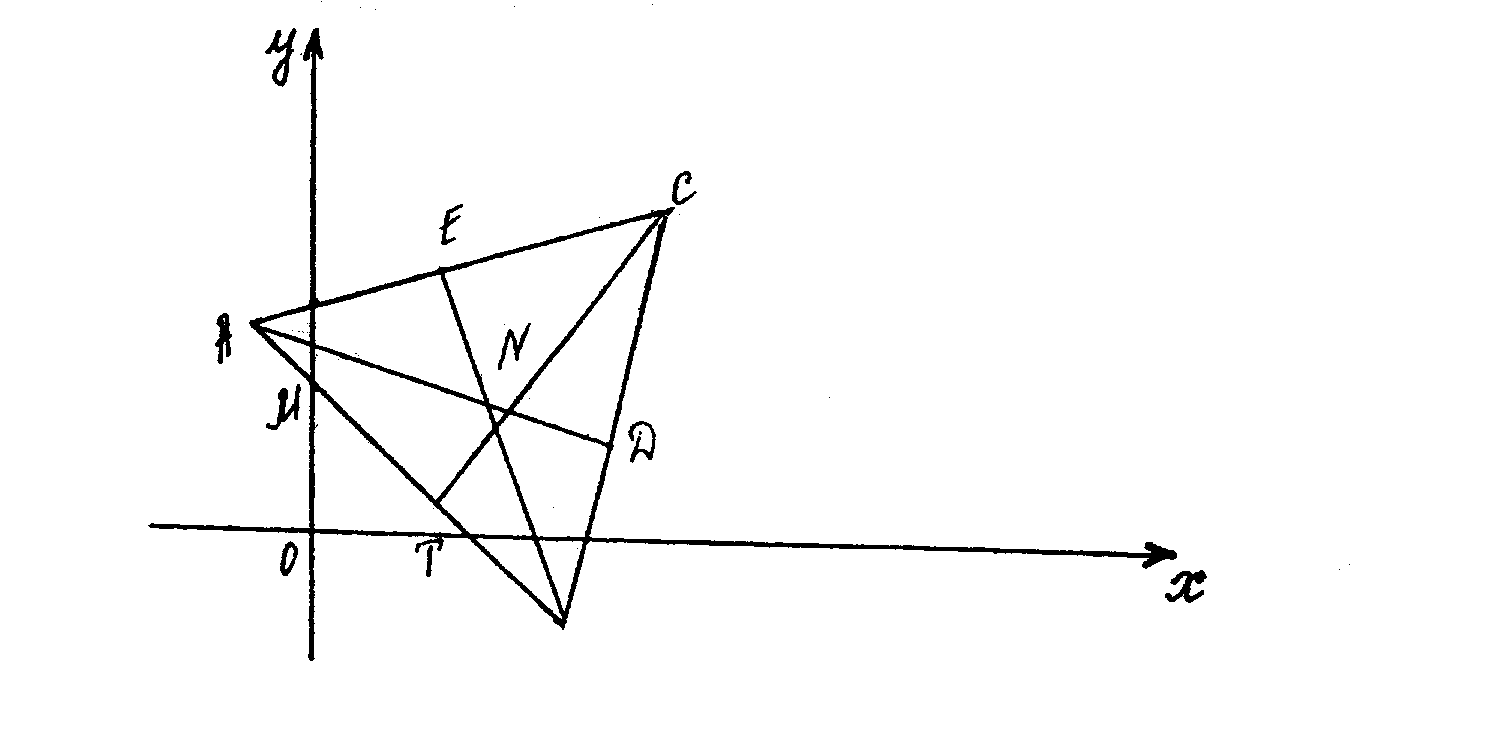
Рис. 1
2. Скласти
канонічне рівняння гіперболи, що
симетрична відносно до осей координат
і проходить через точки
А (8; 2![]() )
і В (–6;
)
і В (–6;
![]() ).
Знайти півосі, фокуси, ексцентриситети
та рівняння асимптоти цієї гіперболи,
а також усі точки перетину гіперболи з
колом, центр якого знаходиться на
початку координат, а радіус R
= 6.
).
Знайти півосі, фокуси, ексцентриситети
та рівняння асимптоти цієї гіперболи,
а також усі точки перетину гіперболи з
колом, центр якого знаходиться на
початку координат, а радіус R
= 6.
► Канонічне рівняння шуканої гіперболи має вигляд
![]() .
(11.6)
.
(11.6)
За умови задачі точки А і В знаходяться на гіперболі, отже координати цих точок задовольняють рівнянню (11.6). Підставляючи в рівняння (11.6) замість поточних координат Х та У координати даних точок, одержуємо систему двох рівнянь відносно до параметрів a і b.
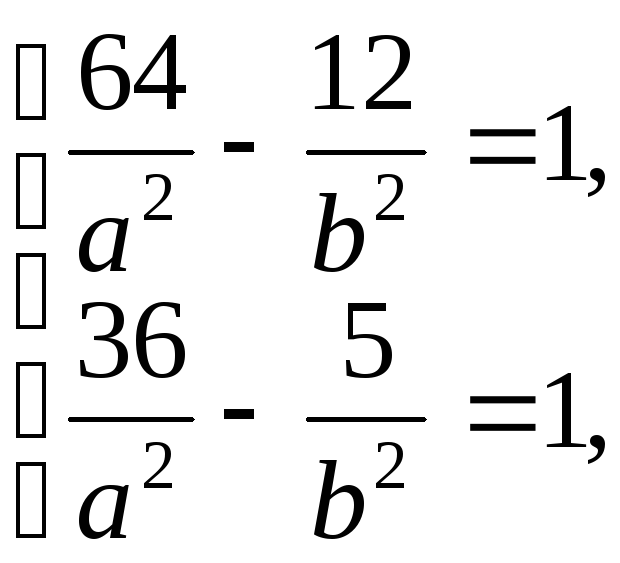 або
або ![]()
Віднімаючи від першого рівняння друге, маємо 28b2 – 7a2 = 0, звідси a2 = 4b2. Після підставляння у перше рівняння маємо: 64b2 – 48b2 = 4b2b2, b2 = 4, тоді a2 = 16.
Шукане рівняння гіперболи має вигляд:
![]() (11.7)
(11.7)
Півосі гіперболи а=4; b=2. Визначаємо фокуси гіперболи F1(–C; 0) i F2(C; 0). Користуючись рівністю c2 = a2 + b2, маємо:
c2
=16+4=20, c =
![]() .
.
Отже,
F1(2![]() ,0)
таF2(–2
,0)
таF2(–2![]() ,0)
– фокуси гіперболи.
,0)
– фокуси гіперболи.
Ексцентриситет гіперболи
визначаємо за формулою
![]() .
.
Рівняння асимптот гіперболи мають вигляд
![]() i
i ![]() .
.
Отже,
![]() i
i![]() шукані рівняння асимптот. Рівняння
кола, центр якого знаходиться на початку
координат, має вигляд
шукані рівняння асимптот. Рівняння
кола, центр якого знаходиться на початку
координат, має вигляд
x2 + y2 = R2.
Враховуючи, що R= 6, маємо
x2 + y2 = 36. (11.8)
Щоб знайти координати точок перетину гіперболи з колом, необхід-но розв’язати сумісно систему рівнянь (11.7) і (11.8).
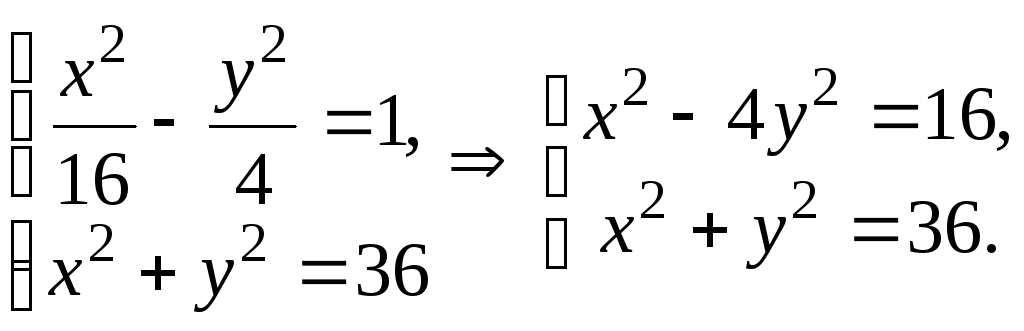
Отже, маємо: 5y2
= 20; y =
2;
x = ![]() .
.
Точки перетину гіперболи з
колом: M1(![]() ;2);M2(–
;2);M2(–![]() ;2);M3(–
;2);M3(–![]() ;2);M4
(
;2);M4
(![]() ;–2).
;–2).
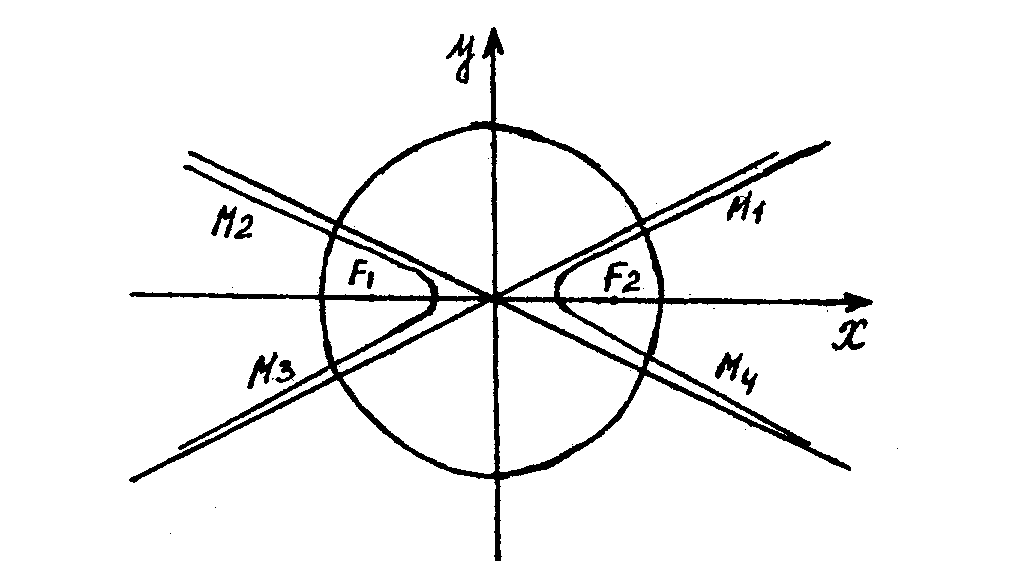
Побудуємо в системі координат ХоУ гіперболу і коло (рис. 2)
![]()
![]()
Рис. 2 ◄
3. Написати рівняння кривої, кожна точка якої знаходиться на однаковій відстані від точки F(4; 3) і прямої у=1. Отримане рівняння привести до простішого виду і побудувати криву.
► Нехай M(x, y) – довільна точка шуканої кривої. Опустимо з неї перпендикуляр до прямої y=1 (Рис.3). Очевидно, абсциса точки В дорівнює абсцисі точки М, а ордината точки В дорівнює 1, тобто B(x, 1). З умови задачі MF = MB. Таким чином, для кожної точки M(x, y) шуканої кривої справедлива рівність
![]()
або
(x – 4)2 + y2 – 6y + 9 = y2 – 2y + 1; (x-4)2=4y-8.
Остаточно,
![]() (11.9)
(11.9)
Геометричним образом отриманого рівняння є парабола з вершиною в точціO1(4, 2). Рівняння параболи зведемо до простішого виду. Для цього нехай х– 4 = Х; у – 2 = У. Тоді рівняння (11.9) перетворюється до виду
Y=![]() .
(11.10)
.
(11.10)
Перенесемо початок координат у точку О1(4, 2), побудуємо нову систему координат ХО1У, вісі якої, відповідно, паралельні осям Ох і Оу.
Рівняння (11.10) є рівнянням параболи з вершиною в точці О1 і віссю симетрії О1У (Рис. 3).
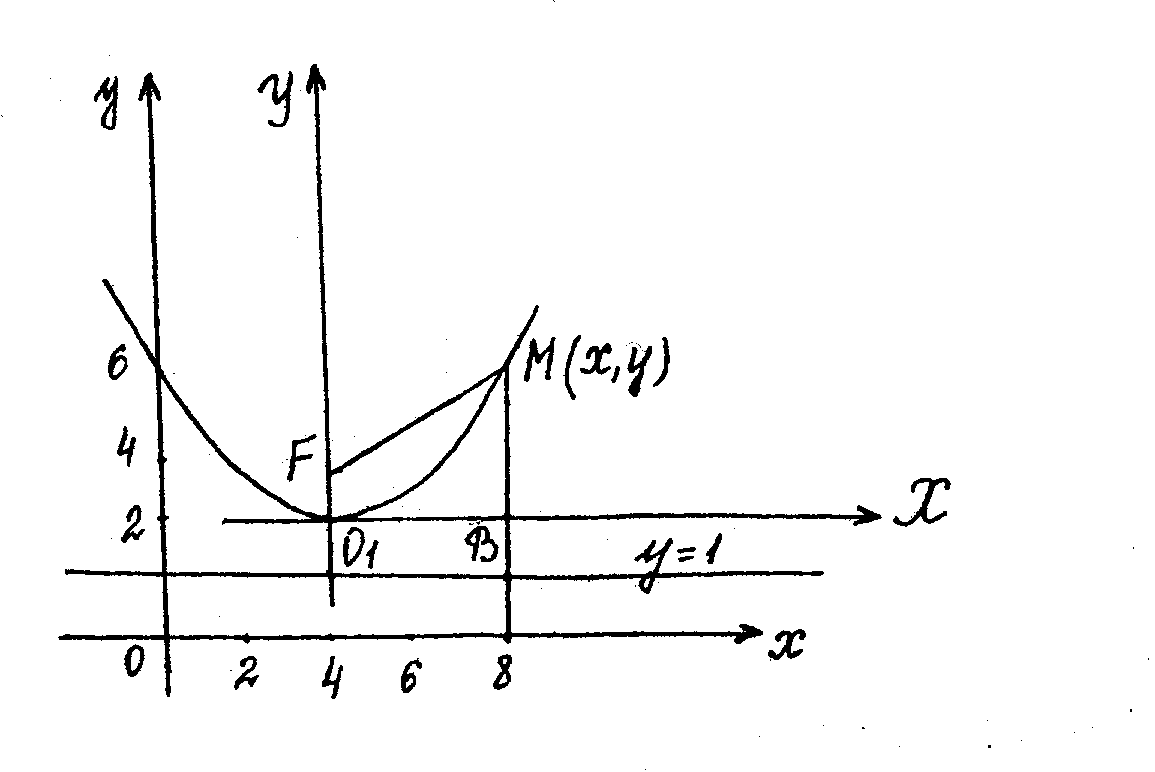
Рис.3 ◄
