9. 10.2 Уравнивание сетей трилатерации коррелатным способом

В сети трилатерации измеренными величинами являются длины сторон. Поэтому при уравнивании должны вычисляться поправки к ним, а затем по уравненным длинам сторон – уравненные значения всех параметров сети.

Наиболее простым способом составления условных уравнений является способ сравнения сумм или разностей углов, вычисленных по измеренным длинам сторон с их значениями, полученными по исходным данным.

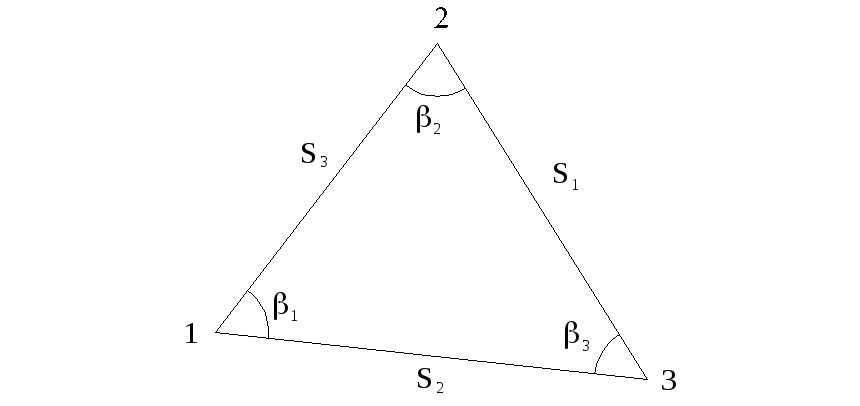
Рисунок 10.2 – Схема для определения углов

Углы удобно вычислять по формулам:

,

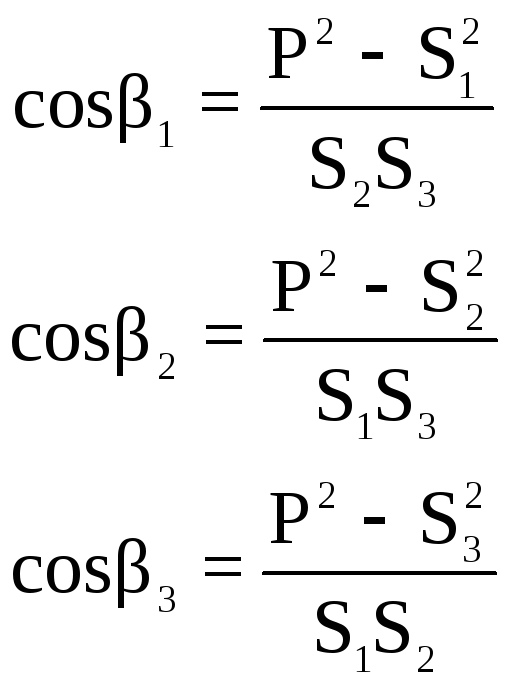где .

Подсчет числа условных уравнений выполняется графическим способом с построением схемы сети по длинам ее сторон. При этом каждой избыточной стороне соответствует одно условное уравнений. Для центральной системы трилатерации можно составить лишь одно условное уравнение:

₁ + ₂ + ₃ + ₄ + ₅ – 360⁰ = 0.

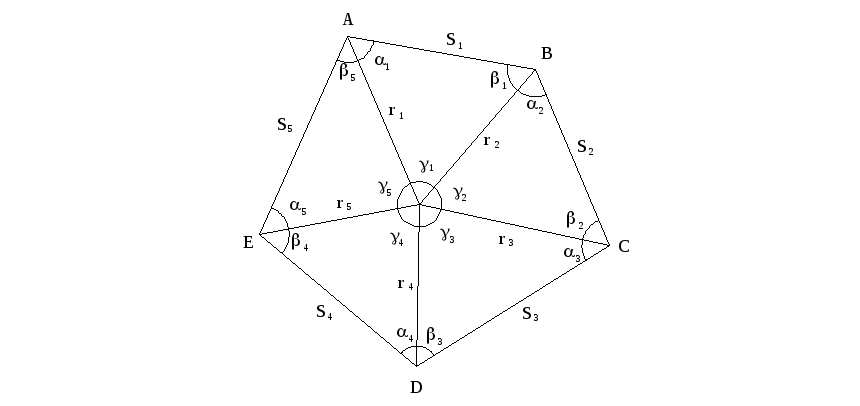
Рисунок 10.3 – Схема центральной системы трилатерации

Обозначим через ’_i углы, вычисленные по измеренным длинам сторон, а поправки к ним – v_i. Тогда:

v_1 + v_2 + v_3 + v_4 + v_5 + w = 0.

где w = ’₁ + ’₂ + ’₃ + ’₄ + ’₅ – 360⁰ – свободный член условного уравнения, выраженный в угловой мере.

Поправки в углы v_i зависимы между собой, поэтому для решения условного уравнения необходимо поправки в углы v_i выразить через поправки в измеренные длины сторон v_Si и v_ri. По теореме косинусов запишем:

S₁² = r₁² + r₂² – 2 r₁ r₂ cos ₁.

Дифференцируя это выражение, получим:

2 S₁ dS₁ = 2 r₁ dr₁ + 2 r₂ dr₂ – 2 r₂ cosγ₁ dr₁ – 2 r₁ cos γ₁ dr₂ + 2 r₁ r₂ sin γ₁ dγ₁

или

S₁ dS₁ = (r₁ – r₂ cosγ₁) dr₁ + (r₂ dr₂– r₁ cos γ₁) dr₂ + r₁ r₂ sin γ₁ dγ₁

Разделим обе части полученного выражения на S₁:

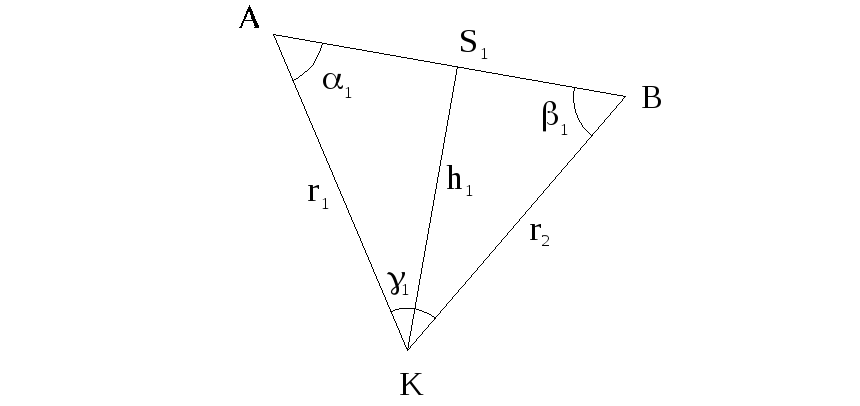
Рисунок 10.4 – Схема

Так как получаем:

Заменив дифференциалы на поправки, получим:

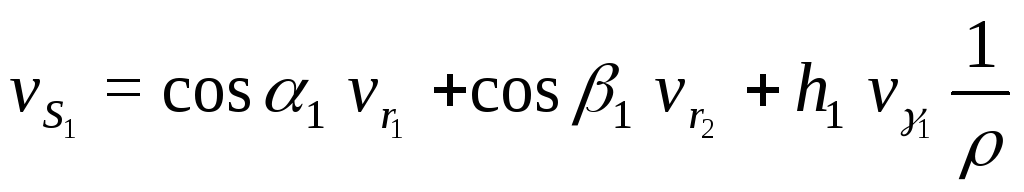
Отсюда:

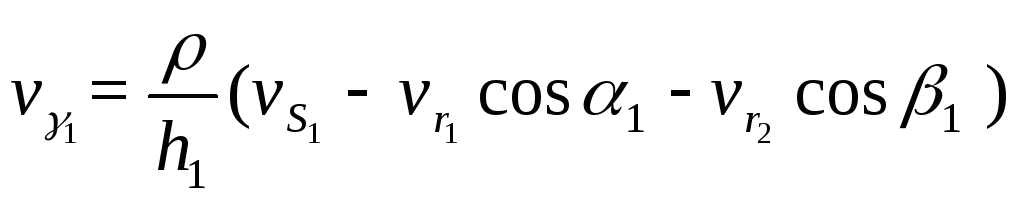
Учитывая, что получаем уравнение:

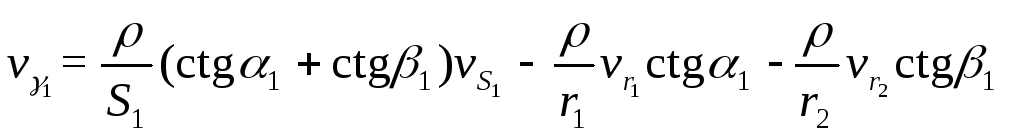
Аналогично для S_i получим:

Подставив эти выражения для поправок в углы γ_i в условное уравнение получим после преобразования:

где

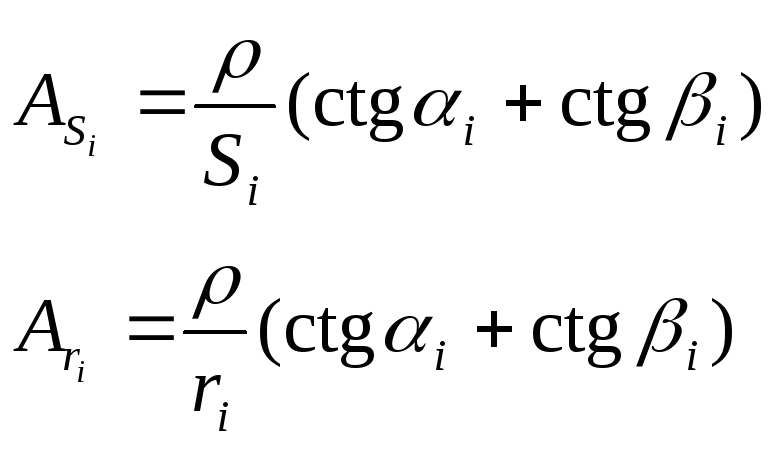
Решение системы условных уравнений выполняется по методу наименьших квадратов, т.е. при условии

где p_S и p_r – веса измеренных длин сторон S и r.

Остальные виды условных уравнений, возникающие в сетях трилатерации, получают аналогично:

- составляется условное уравнение, связывающее углы треугольников;

- решаются треугольники по измеренным длинам сторон;

- вычисляется невязка условного уравнения в угловой мере;

- выражается при помощи формулы 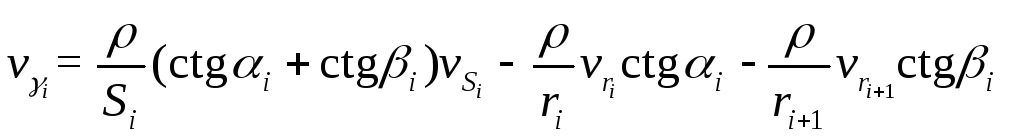поправки в углы через поправки в длины сторон;

- приводятся подобные члены полученных уравнений и окончательно составляются условные уравнения;

- методом наименьших квадратов решается система условных уравнений и вычисляются поправки в измеренные длины сторон.

10.3 Уравнивание сетей трилатерации параметрическим способом

Для составления параметрических уравнений поправок выразим длину линии между точками k и i через координаты начальной и конечной точек:

.

Частные производные по x и y имеют вид:

Следовательно,

Для каждой измеренной стороны имеем:

где - уравненное значение длины стороны между пунктами k и i;

- предварительное значение длины этой же стороны, вычисленное по предварительным координатам точек;

- измеренное значение длины стороны между точками k и i;

- поправка к предварительной длине стороны;

- поправка в измеренную длину стороны.

Следовательно, или

где - свободный член параметрического уравнения.

Таким образом, параметрические уравнения поправок имеют вид:

Если один из пунктов является исходным, то для этого пункта равны 0. Система параметрических уравнений поправок решается при условии , при этом, вначале вычисляются поправки в предварительные координаты и их уравненные значения. Затем вычисляются поправки в измеренные длины сторон v_S. По уравненным длинам сторон осуществляется контроль уравнительных вычислений.

Предварительные координаты пунктов трилатерации могут быть найдены по формулам:

где

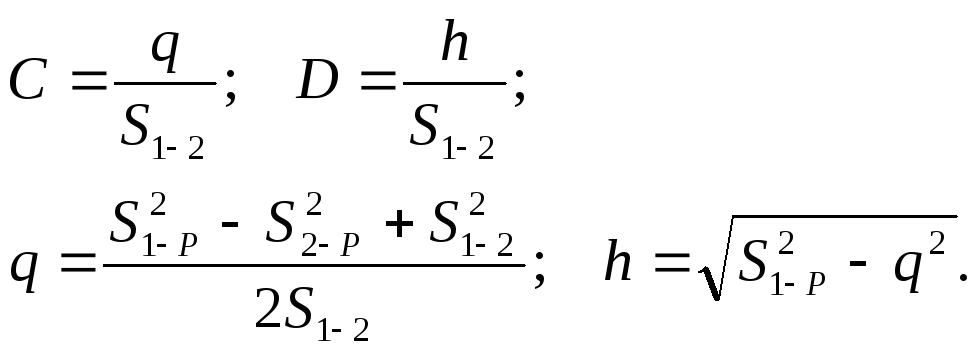
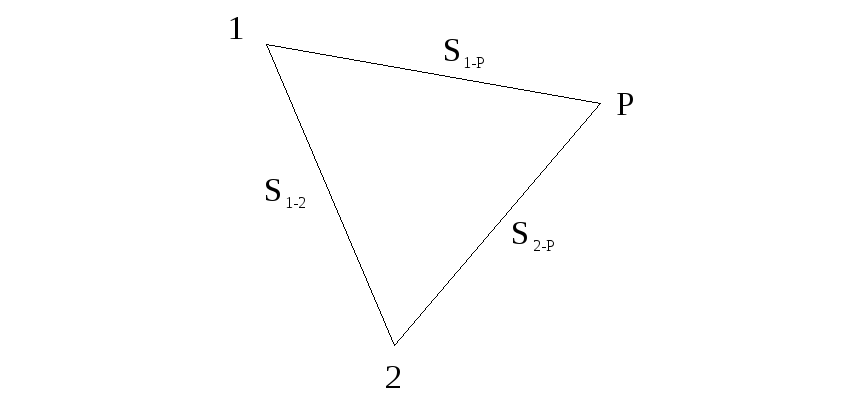
Рисунок 10.5 – Схема для определения предварительных координат пунктов трилатерации