8.2 Определение числа условных уравнений

Для подсчета числа и составления условных уравнений удобно использовать графический прием, заключающийся в следующем. Рассматривая сеть триангуляции как свободную, т.е. имеющую лишь два исходных пункта, строят схему сети, на которой показывают только те углы, которые необходимы для определения всех пунктов, включая и твердые.

Построенная сеть не будет содержать избыточные измерения, а следовательно, не будет иметь условных уравнений. Углы, не использованные для построения этой сети, являются избыточными. Каждому из них будет соответствовать условное уравнение. Вводя последовательно избыточные углы и отмечая их на схеме сети, легко определить все возникающие при этом условия.

В свободных сетях триангуляции число условных уравнений определяется по формуле:

R₁ = N – 2n + 4,

где N – общее число измеренных углов;

п – общее число пунктов сети, включая и твердые (исходные) пункты.

Избыточные исходные данные (базисные стороны, азимуты, дирекционные углы, координаты пунктов) приводят к дополнительным условным уравнениям. Отмечая на схеме те исходные данные, которые не использованы при ее построении, последовательно определяются соответствующие им условные уравнения. При этом каждая избыточная базисная сторона дает одно уравнение базиса, каждый избыточный азимут или дирекционный угол – одно азимутальное уравнение.

Число условных уравнений координат равно удвоенному числу избыточных групп или отдельных твердых пунктов, не связанных друг с другом твердыми сторонами плюс удвоенное число замкнутых цепей треугольников (полигонов). Т.е. в несвободной сети триангуляции число условных уравнений будет равно:

R₂ = N – 2n + q + 4 = R₁ + q,

где q – число условных уравнений, отвечающих избыточным исходным данным.

Число полюсных уравнений определяется по формуле:

Р = L – 2n + 3,

где L – число всех линий в сети триангуляции;

п – число всех пунктов сети.

Число уравнений фигур и горизонтов будет равно:

с = R₁ – p = N – L + 1,

где N – общее число измеренных углов;

L – общее число всех линий в сети триангуляции.

Число уравнений горизонта g равно числу центральных пунктов сети, вокруг которых углы измерены с замыканием горизонта, т.е. на 360⁰. Тогда число уравнений фигур будет равно:

f = c – g = N – L – g + 1 или

f = l – n + 1,

где l – число сплошных линий в сети (т.е. линий, по которым направления измерены в двух крайних точках линии);

п – число всех пунктов в сети.

Вычислитель должен из всех возможных условных уравнений выбрать только необходимые и независимые условные уравнения.

8.3 Уравнивание сетей триангуляции

При уравнивании триангуляции по углам могут возникнуть семь типов условных уравнений:

1. условие фигур;

2. условие суммы углов;

3. условие горизонта;

4. условие полюса;

5. условие твердых дирекционных углов;

6. условие базисов;

7. условие координат.

Совместное решение условных уравнений методом наименьших квадратов является общим, но не самым простым приемом решения задачи. При совместном решении условных уравнений необходимо решить систему нормальных уравнений в сети.

Например, при уравнивании углов в цепочке из 10 треугольников, опирающихся на две пары исходных пунктов будем иметь:

1. 10 условных уравнений фигур;

2. 2 условных уравнения координат;

3. 1 условное базисное уравнение;

4. 1 условное азимутальное уравнение.

Т.е. будем иметь систему нормальных уравнений 14 порядка.

Упрощение процедуры уравнивания достигается применением группового уравнивания. При уравнивании триангуляции наибольшее применение находит двухгрупповой способ.

В общем случае двухгрупповой способ уравнивания не проще совместного решения всех условных уравнений. Но в частных случаях удается существенно сократить вычисления. Наибольший эффект получается при включении в первую группу только условных уравнений фигур с коэффициентами, равными единице. В этом случае решение условных уравнений 1-й группы сводится к распределению невязки каждого уравнения поровну на все входящие в него углы. Упрощаются и все остальные вычисления.

Система условных уравнений поправок

A V + W = 0

преобразуется в систему нормальных уравнений:

(A Q A^T) K + W = 0

где А – матрица коэффициентов условных уравнений, состоящая из п столбцов и k строк;

п – число измеренных углов;

k – число условных уравнений;

Q = P^-1 – обратная весовая матрица (при равноточных измерениях углов Q = E и ее можно не учитывать, т.е. A Q A^T = А А^Т);

W – вектор невязок в условных уравнениях.

При решении нормальных уравнений вычисляются коррелаты:

K = - (A Q A^T)^-1 W.

Поправки в измеренные углы вычисляются по формуле:

V = Q K A^T.

По вычисленным уравненным углам х* = х + v окончательно решаются треугольники и вычисляются уравненные координаты всех определяемых пунктов сети триангуляции. Средняя квадратическая погрешность единицы веса вычисляется по формуле:

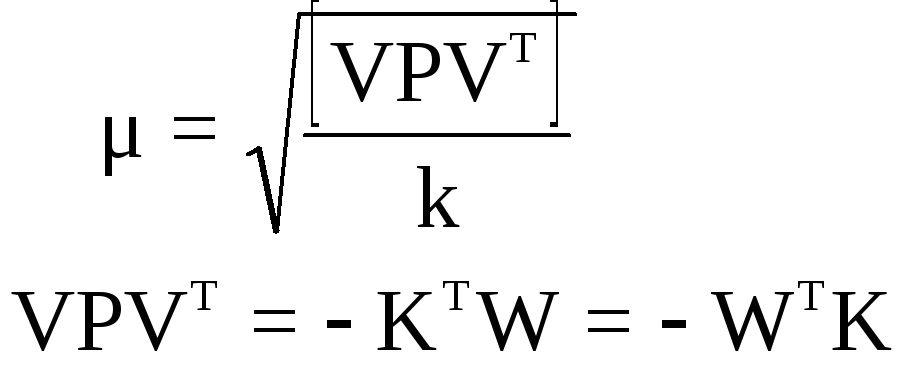
а средняя квадратическая погрешность функции F по формуле:

.