
nasyrov_a_z_nasyrov_z_h_diskretnaya_matematika
.pdf| [AG UGLUBLENIQ; ESLI VE TAKOJ WER[INY S := S n fxg , B := B [ fxg | [AG WOZWRATA.
3) eSLI S = ? I A = ? , TO, W \TOM SLU^AE, B = X I OBHOD GRAFA ZAWER[EN.
dLQ OBHODA GRAFA G(X; ;) W [IRINU OBRAZU@T MNOVESTWO A NERASSMOTRENNYH WER[IN, MNOVESTWO B RASSMOTRENNYH WER[IN I O^EREDX T AKTIWNYH WER[IN. nA STARTE A = X , B = ? , T = ? . aLGORITM OBHODA PREDPOLAGAET WYPOLNENIE SLEDU@]IH [AGOW.
1) eSLI T = ? , A 6= ? , TO WYBIRAEM PROIZWOLXNU@ WER[INU x 2 A I IZMENQEM A := A n fxg , T := T [ fxg . |TOT [AG WYPOLNQETSQ W NA^ALE OBHODA KAVDOJ KOMPONENTY SWQZNOSTI GRAFA G .
|
|
6 |
2) eSLI |
T = ? I x | PERWAQ WER[INA O^EREDI T , TO NAHODIM |
|
WER[INU y |
2 |
A TAKU@, ^TO (x; y) 2 ; I IZMENQEM A := A n fyg , |
T := T [ fyg |
| [AG RAS[IRENIQ; ESLI VE TAKOJ WER[INY y NET, |
|
TO IZMENQEM T := T n fxg , B := B [ fxg | KONEC RAS[IRENIQ IZ |
||
WER[INY x . |
|
|
3) eSLI |
T = ? I A = ? , TO, W \TOM SLU^AE, B = X I OBHOD |
|
GRAFA ZAWER[EN.
zADA^A O KRAT^AJ[IH PUTQH W GRAFE. gRAF G(X; ;) NAZYWAETSQ WZWE[ENNYM, ESLI KAVDOMU EGO REBRU (xi; xj) PRISWOENO ^ISLO l(xi; xj) , KOTOROE MY BUDEM S^ITATX DLINOJ \TOGO REBRA. zADA^A O KRAT^AJ[IH PUTQH SOSTOIT W TOM, ^TOBY NAJTI CEPX NAIMENX[EJ DLINY, SOEDINQ@]U@ DWE DANNYE WER[INY a I b SWQZNOGO GRAFA. aLGORITM RE[ENIQ \TOJ ZADA^I PREDPOLAGAET WYPOLNENIQ SLEDU@- ]IH [AGOW.
1)kAVDOJ WER[INE x PRISWOIM NA^ALXNU@ METKU m(x) PO PRA-
WILU: m(a) = 0 , m(x) = 1 , PRI x 6= a .
2)iZMENENIE METOK. pOKA SU]ESTWUET REBRO (x; y) TAKOE, ^TO m(y) > m(x) + l(x; y) , WYPOLNQETSQ m(y) := m(x) + l(x; y) .
pO HODU RABOTY PUNKTA 2) m(x) < 1 RAWNA DLINE NEKOTOROJ CEPI, SOEDINQ@]EJ WER[INU x S WER[INOJ a , A PO OKON^ANI@ RABOTY [AGOW 1) I 2) m(x) RAWNA DLINE KRAT^AJ[EJ CEPI, SOEDINQ@]EJ WER[INY x I a .
pOSTROENIE KRAT^AJ[EJ CEPI b = x0 ! x1 ! : : : ! xn = a SOSTOIT W NAHOVDENII SLEDU@]EJ POSLE xi WER[INY xi+1 PO FOR-
61
MULE m(xi+1) = m(xi) ; l(xi; xi+1) , DLQ i = 0; 1; : : : ; n ; 1 , POKA NE
POLU^IM xn = a .
uPRAVNENIQ PO TEORII GRAFOW
117.pRIWEDITE PRIMER GRAFA S WER[INAMI x1; x2 ; x3 TAKOGO, ^TO deg x1 = 3 , deg x2 = 4 , deg x3 = 5 . dLQ POSTROENNOGO GRAFA NAJDITE EGO MATRICU SMEVNOSTI.
118.dLQ GRAFA, IZOBRAVENNOGO NA RIS. 18, UKAVITE SPISKI SMEVNYH WER[IN.
119.pUSTX DANY NEOTRICATELXNYE CELYE ^ISLA s1; s2; : : : ; sn TA-
n
KIE, ^TO P si = 2m . pOSTROJTE GRAF S WER[INAMI x1; x2 ; : : : ; xn
i=1
TAK, ^TOBY deg xi = si PRI i = 1; 2; : : : ; n .
120.pOSTROJTE PROSTOJ GRAF S WER[INAMI x1 , x2 , x3 , x4 TAKOJ,
^TO deg x1 = deg x2 = 2 , deg x3 = deg x4 = 3 .
121.sKOLXKO REBER IMEET POLNYJ GRAF Kn ?
122.nAJDITE KOLI^ESTWO REBER GRAFA On + Km;n .
odOKAVITE, ^TO + = .
123.Km Kn Km+n
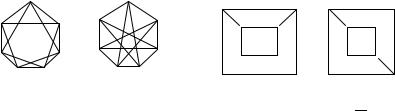
124.sKOLXKIMI SPOSOBAMI MOVNO GRAF G1 , (SM. RIS. 30), IZOMORF-
NO OTOBRAZITX NA GRAF G2 ?
125. dLQ GRAFA G1 , (SM. RIS. 30), NAJDITE DOPOLNITELXNYJ GRAF.
a |
|
a |
G1 a |
a |
a |
G2 a |
b |
b |
b |
b |
b |
b |
Gb |
b |
||
a |
|
|
|
a |
a |
|
|
a |
|
|
G1 |
|
|
|
2 |
|
a |
|
a |
a |
a |
|
b |
b |
|
|
b |
b |
|
||||
|
|
|
|
|
b |
|
rIS. b31 |
b |
|
|
b |
|||||
|
|
|
rIS. 30 |
|
|
|
|
|
|
|
||||||
126.pRIWEDITE PRIMER GRAFA G IZOMORFNOGO GRAFU G.
127.wYQSNITE PLANARNOSTX GRAFA O3 + K2;2 .
128.pRI KAKIH m; n GRAF Km;n QWLQETSQ PLANARNYM?
62
o |
pRI KAKIH n GRAF Kn |
QWLQETSQ PLANARNYM? |
129. |
||
130. rEALIZUJTE GRAF K3;3 |
NA POWERHNOSTI TORA. |
|
o |
rEALIZUJTE NA POWERHNOSTI TORA GRAFY K5 I K6 . |
|
131. |
||
132.kAKOE NAIMENX[EE ^ISLO KOMPONENT SWQZNOSTI MOVET IMETX GRAF, U KOTOROGO 100 WER[IN I 60 REBER?
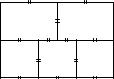
133.rASSTOQNIEM MEVDU WER[INAMI GRAFA NAZYWAETSQ MINIMALXNAQ DLINA CEPI, SOEDINQ@]EJ \TI WER[INY. dIAMETROM SWQZNOGO GRAFA NAZYWAETSQ RASSTOQNIE MEVDU SAMYMI UDALENNYMI EGO WER- [INAMI. nAJDITE DIAMETRY GRAFOW, IZOBRAVENNYH NA RIS. 31.
134.pLOSKIJ SWQZNYJ GRAF IMEET TOLXKO TREUGOLXNYE GRANI. dO-
KAVITE DLQ \TOGO GRAFA RAWENSTWA m = 3n ; 6 I l = 2n ; 4 .
o pLOSKIJ SWQZNYJ GRAF IMEET TOLXKO ^ETYREHUGOLXNYE GRANI.
135.
dOKAVITE DLQ \TOGO GRAFA RAWENSTWA m = 2n ; 4 I l = n ; 2 .
136.pRI KAKIH n QWLQETSQ \JLEROWYM GRAF Kn ?
137.pRI KAKIH m I n QWLQETSQ \JLEROWYM GRAF Km;n ?
138.gRAF G NAZYWAETSQ POLU\JLEROWYM, ESLI IMEETSQ PROSTAQ NEZAMKNUTAQ CEPX, SODERVA]AQ WSE REBRA GRAFA G . dOKAVITE, ^TO SWQZNYJ GRAF QWLQETSQ POLU\JLEROWYM TOGDA I TOLXKO TOGDA, KOGDA ON IMEET ROWNO DWE NE^ETNYE WER[INY, PRI^EM \TI WER[INY SLUVAT KONCAMI PROSTOJ CEPI, SODERVA]EJ WSE REBRA GRAFA.
139.nA RIS. 32 POKAZANA PLANIROWKA DOMA IZ PQTI KOMNAT. iME-
@TSQ |
|
DWERI IZ L@BOJ KOMNATY W L@BU@ SOSED- |
|
N@@ KOMNATU I NA ULICU. wNA^ALE WSE |
|
DWERI OTKRYTY, NO PRI PROHOVDENII ^E- |
|
REZ L@BU@ DWERX, ONA AWTOMATI^ESKI ZA- |
|
KRYWAETSQ. mOVNO LI ODNOMU ^ELOWEKU |
|
ZAKRYTX WSE DWERI? |
rIS. 32 |
140. sKOLXKO IMEETSQ DEREWXEW S PQTX@ I S [ESTX@ WER[INAMI? pOSTROJTE IH.
63
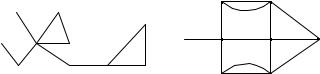
o dOKAVITE, ^TO, ESLI DLQ SWQZNOGO GRAFA WYPOLNENO RAWENSTWO
141.
m = n ; 1 , TO ON QWLQETSQ DEREWOM.
o |
|
|
142. sKOLXKO IMEETSQ KORNEWYH DEREWXEW S PQTX@ WER[INAMI? pO- |
||
STROJTE IH. |
|
|
143. nAJDITE CIKLOMATI^ESKOE ^ISLO GRAFA |
||
A) K3;3 , |
B) Kn , |
W) O4 + K2;5 . |
o |
iZWESTNO, ^TO (G) = 2 . kAKOE NAIBOLX[EE KOLI^ESTWO CIK- |
144. |
LOW MOVET IMETX \TOT GRAF?
145.nAJDITE HROMATI^ESKOE ^ISLO GRAFA K4 + K3 + K2;1 .
146.dOKAVITE, ^TO, ESLI GRAF G IMEET k KOMPONENT SWQZNOSTI
G1; G2; : : : ; Gk , TO (G) = max( (G1); (G2); : : : ; (Gk) .
dOKAVITE, ^TO (G) = 2 TOGDA I TOLXKO TOGDA, KOGDA G | NENULEWOJ GRAF, QWLQ@]IMSQ ^ASTI^NYM DLQ
148. rEALIZUJTE ALGORITM OBHODA W GLUBINU I W [IRINU DLQ GRAFA, IZOBRAVENNOGO NA RIS. 33.
o rEALIZUJTE ALGORITM OBHODA W GLUBINU I W [IRINU DLQ GRAFA,
149.
IZOBRAVENNOGO NA RIS. 34.
2 |
|
3 |
|
|
5k |
-4} |
|
|
|
|
|
|
10 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
-7 |
-8 |
- |
3 |
1 |
7 |
4 |
|
|
6 |
6 |
3 |
|
|
|
|
|
1 + |
- 2 |
|
|
|
6 |
|
5 |
8 |
9 |
|
|
||
|
|
rIS. 33 |
|
|
rIS. 34 |
|
|
|
64

metodi~eskie ukazaniq po re{eni` zada~
zADA^A 1
nAJTI MNOGO^LEN vEGALKINA, REALIZU@]IJ BULEWU FUNKCI@ f(a; b; c; d) = (3 ; 8; 12; 15) , ZADANNU@ STOLBCOM ZNA^ENIJ W STANDARTNOJ TABLICE ISTINNOSTI.
rE[ENIE
sTANDARTNAQ TABLICA ISTINNOSTI DLQ \TOJ FUNKCII, SM. TABL. 9,
IMEET 16 STRO^EK. dLQ NAHOVDENIQ MNOGO- |
|
tABLICA 9 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
^LENA vEGALKINA NAPI[EM FORMULU (3) NA |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
c |
d |
f |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
S. 9, ISPOLXZUQ TOLXKO TE STRO^KI, NA KOTO- |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
0 |
0 |
0 |
0 |
0 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
RYH FUNKCIQ f QWLQETSQ ISTINNOJ. w RE- |
0 |
0 |
0 |
1 |
0 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ZULXTATE POLU^ITSQ FORMULA f(a; b; c; d) = |
0 |
0 |
1 |
0 |
0 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
abcd |
abcd abcd abcd abcd abcd |
0 |
0 |
1 |
1 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
abcd abcd . dALEE, UPROSTIM \TU FORMU- |
0 |
1 |
0 |
0 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||
LU, ISPOLXZUQ SWOJSTWA xy xz = x(y z) |
0 |
1 |
0 |
1 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||
I x |
x |
|
= 1 . sDELAEM SLEDU@]IE PREOBRA- |
0 |
1 |
1 |
0 |
1 |
|||||||||||||||||||||||||||||||||||||||||||
ZOWANIQ: |
f(a; b; c; d) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
abcd abc(d d) |
0 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
abc(d d) acd(b |
b) abcd = abcd abc |
1 |
0 |
0 |
0 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
abc |
|
acd abcd |
= |
abcd ab(c c) acd abcd = |
1 |
0 |
0 |
1 |
0 |
||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
abcd ab acd abcd . dALEE, ZAMENQEM OT- |
1 |
0 |
1 |
0 |
0 |
||||||||||||||||||||||||||||||||||||||||||||||
RICANIQ PEREMENNYH PO FORMULE |
x |
= x 1 , |
1 |
0 |
1 |
1 |
0 |
||||||||||||||||||||||||||||||||||||||||||||
RASKRYWAEM POLU^IW[IESQ SKOBKI I PRIWO- |
1 |
1 |
0 |
0 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||
DIM PODOBNYE ^LENY PO FORMULE x x = 0 : |
|||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
1 |
0 |
1 |
0 |
|||||||||||||||||||||||||||||||||||||||||||||||
f(a; b; c; d) |
= (a 1)(b 1)cd (a 1)b |
1 |
1 |
1 |
0 |
0 |
|||||||||||||||||||||||||||||||||||||||||||||
a(c 1)(d 1) abcd = abcd acd bcd |
1 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||
cd ab b acd ac ad a abcd = = bcd ab ac ad cd a b .
oTWET. f(a; b; c; d) = bcd ab ac ad cd a b .
65

|
dANNAQ FORMULA IMEET SLEDU@]IE PODFORMULY: A = a b , |
|||||||||||||||||
B = a c , C = b ! B , D = A C , E = |
c |
|
, F = a ! E , G = F |
I, |
||||||||||||||
NAKONEC, |
g(a; b; c) = D |
_G . sOSTAWIM TABLICU ISTINNOSTI DLQ WSEH |
||||||||||||||||
\TIH PODFORMUL, SM. TABL. 10, ISPOLXZUQ OPREDELENIQ LOGI^ESKIH |
||||||||||||||||||
OPERACIJ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
tABLICA 10 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
B |
|
C |
D |
|
E |
F |
G |
g |
|
|
|||
|
a b |
a c |
b ! B |
A C |
|
|
|
a ! E |
F |
D _ G |
|
|
||||||
a b c |
|
|
|
c |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
0 |
0 |
|
1 |
0 |
|
1 |
1 |
|
1 |
1 |
0 |
1 |
|
|
|||
0 |
0 |
1 |
|
1 |
1 |
|
1 |
1 |
|
0 |
1 |
0 |
1 |
|
|
|||
0 |
1 |
0 |
|
0 |
0 |
|
0 |
0 |
|
1 |
1 |
0 |
0 |
|
|
|||
0 |
1 |
1 |
|
0 |
1 |
|
1 |
0 |
|
0 |
1 |
0 |
0 |
|
|
|||
1 |
0 |
0 |
|
0 |
1 |
|
1 |
0 |
|
1 |
1 |
0 |
0 |
|
|
|||
1 |
0 |
1 |
|
0 |
0 |
|
1 |
0 |
|
0 |
0 |
1 |
1 |
|
|
|||
1 |
1 |
0 |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
0 |
1 |
|
|
|||
1 |
1 |
1 |
|
1 |
0 |
|
0 |
0 |
|
0 |
0 |
1 |
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wREZULXTATE IMEEM STOLBEC ZNA^ENIJ g(a; b; c) = (0; 1; 5; 6; 7) =
=(1100 0111)T .
pEREHODIM K NAHOVDENI@ MINIMALXNOJ dnf. wNA^ALE NAJDEM WSE PROSTYE KON_@NKTY FUNKCII g , PRIMENQQ PRAWILO SKLEIWANIQ
AB _ AB = A .
nABORY 0; 1; 5;6; 7 , NA KOTORYH g RAWNA 1, ZAPI[EM, SORTIRUQ IH W GRUPPY PO KOLI^ESTWU EDINIC, I NAHODIM WSE WARIANTY DLQ PRIMENENIQ PRAWILA SKLEIWANIQ (SKLEIWA@]IESQ STRO^KI NAHODQTSQ W SOSEDNIH GRUPPAH). w REZULXTATE, SKLEIWANIEM KON_@NKTOW (0) I (1), (1) I (5), (5) I (7), (6) I (7), POLU^IM ZAMENQ@]IE IH KON_@NKTY
(0; 1) = 00; , (1; 5) = ;01 , (5; 7) = 1 ;1 , (6; 7) = 11; . kON_@NKTY
(0), (1), (5), (6) I (7) W REZULXTATE SKLEIWANIQ PROPALI. w ITOGE, OSTALISX ^ETYRE KON_@NKTA: 00; , ;01 , 1 ; 1 I 11; . pRAWILO
66

SKLEIWANIQ PRIMENITX K NIM NEWOZMOVNO I W REZULXTATE POLU^I-
LASX |
|
SOKRA]ENNAQ dnf: g(a; b; c) = (00;) _(;01) _(1 ;1) _(11;) = |
||||||||||||||||||
|
||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ab _ bc _ ac _ ab . |
|
|
|
|
|
|
tABLICA 11 |
|
|
|
||||||||||
(0) |
000 |
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
|
||||
|
(0,1) |
00- |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
(1) |
001 |
|
|
|
|
|
|||||||||||||
|
(1,5) |
-01 |
|
|
|
|
|
|
0 |
1 |
1 |
1 |
0 |
|
||||||
(5) |
101 |
|
|
|
|
|
|
|
||||||||||||
|
00 |
|
|
|
1 |
1 |
|
|
|
|
||||||||||
(5,7) |
1-1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(6) |
110 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
(6,7) |
11- |
|
1 |
|
|
1 |
|
|
1 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(7) |
111 |
|
|
; |
|
|
|
|
|
1 |
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
11; |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
;01 |
|
|
1 |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
pO TABLICE ISTINNOSTI DLQ PROSTYH KON_@NKTOW WIDNO (SM. TABL. 11), ^TO KON_@NKTY ab I ab NELXZQ UDALITX, A IZ DWUH OSTAW- [IHSQ KON_@NKTOW MOVNO ODNOGO UDALITX, T.E. g(a; b; c) IMEET DWE
MINIMALXNYE dnf: g(a; b; c) = ab _ bc _ ab = ab _ ac _ ab .
dLQ POSTROENIQ KONTAKTNOJ SHEMY, FUNKCIEJ PROWODIMOSTI KOTOROJ QWLQETSQ FUNKCIQ g(a; b; c) , WOZXMEM ODNU IZ MINIMALXNYH
dnf, NAPRIMER, g(a; b; c) = |
a |
b _ ac _ ab . |
+ |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
r |
|
|
|
r |
|
|||||||||||||
eSLI PO \TOJ dnf POSTROITX SHEMU, TO ONA |
|
|
|
|
a |
|
|
|
|||||||||||||
|
|
b |
|
|
|
||||||||||||||||
BUDET SOSTOQTX IZ 6 KONTAKTOW, ESLI VE \TU |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
rb |
|
|
|
r |
|
||||||||||||
dnf PREDWARITELXNO PREOBRAZOWATX TAK: |
|
|
|
|
|
|
c |
|
|||||||||||||
|
|
a |
|
|
|
||||||||||||||||
f(a; b; c) = |
a |
b _ a(c _ b) , TO MOVNO POSTRO- |
; |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
r |
|
|
r |
r |
||||||||||||||
ITX SHEMU IZ |
5 |
KONTAKTOW |
, |
IZOBRAVENNU@ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
rIS. 35 |
|
|
|
|||||
NA RIS. 35. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
zADA^A 3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|||||||||||||||||
dOKAZATX RAWENSTWO (A n B)4(A [ C) = A \ (B4C) , GDE A , |
B , |
||||||||||||||||||||
C { PROIZWOLXNYE MNOVESTWA. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
rE[ENIE
dLQ DOKAZATELXSTWA PRIMENIM METOD KRUGOW |JLERA, SM. RIS. 36. iZOBRAZIM DANNYE MNOVESTWA KRUGAMI TAK, ^TOBY ONI RAZBIWALI PLOSKOSTX NA 8 ^ASTEJ. iZ \TO- GO RISUNKA WIDNO, ^TO A n B = M4 [ M5 ,
A [ C = M0 [ M1 [ M2 [ M3 [ M5 [ M7 I
TOGDA MNOVESTWO W LEWOJ ^ASTI RAWENSTWA
67
AB
M6
M4 M2
M7
M5 M3
M1
CM0
rIS. 36

= (M4 [M5)4(M0 [M1 [M2 [M3 [M5 [M7) = = M0 [ M1 [ M2 [ M3 [ M4 [ M7) .
dALEE, IZ RISUNKA WIDNO, ^TO B4C = M1 [ M2 [ M5 [ M6 ,
A \ (B4C) = (M4 [ M5 [ M6 [ M7) \ (M1 [ M2 [ M5 [ M6) = = M5 [M6 . tOGDA RP = M5 [ M6 = M0 [ M1 [ M2 [ M3 [M4 [M7 .
mY WIDIM, ^TO OBA MNOVESTWA SOSTOQT IZ ODNIH I TEH ^ASTEJ, \TO I DOKAZYWAET IH RAWENSTWO.
zADA^A 4
|
|
pUSTX DANY BINARNYE OTNO[ENIQ R1 A P I R2 B P , GDE |
||||||||||||||||||||||||||||||||||||||||||||||||
A = |
f |
a; b; c |
|
|
|
, B = |
|
x; y; z |
g |
, |
P = |
f |
p; q; r; t |
. nAJTI KOMPOZICI@ OT- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
g |
|
|
R; |
1 f |
ESLI |
|
= |
f |
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
, |
|||||||||||||||
NO[ENIJ |
R1 |
|
|
, |
R1 |
(a; q); (b; p);(b; q);(b; r);(c; r); (c; t) |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
R2 = f(y; p); (y; q); (y; r);(y; t); (z; r); (z; t)g . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rE[ENIE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
pOSKOLXKU |
|
|
|
|
POLU^AETSQ IZ DEKARTOWA PROIZWEDENIQ |
A P |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
R1 |
||||||||||||||||||||||||||||||||||||||||||||||
UDALENIEM WSEH PAR, WHODQ]IH W |
R1 , TO R1 |
|
= (A 1 |
P ) n |
R1 |
|
= |
|||||||||||||||||||||||||||||||||||||||||||
= |
|
(a; q); (a; r); (a; t); (b; t); (c; p); (c; q) . oTNO[ENIE R; |
POLU^AET- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SOSTAWLQ@]IH OTNO- |
|||||||||||||||
SQ IZ R2 |
PERESTANOWKOJ KOORDINAT WSEH PAR, |
|||||||||||||||||||||||||||||||||||||||||||||||||
[ENIE R2 ; T.E. R;1 |
= |
|
(p; y); (q; y); (r; y);(t; y); (r; z);(t; z) . kOMPO- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
R; |
1 |
|
|
|
2 |
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|||||||
ZICIQ R1 |
|
= |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
(a; y);(a; z); (b; y); (b; z);(c; y) |
. oB_QSNQETSQ \TOT |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
pOSKOLXKU (a; p) |
|
|
|
|
|
|
|
|
|
|
R; |
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 , A |
(p; y) |
|
, |
||||||||||||||||||||||
OTWET SLEDU@]IM OBRAZOM. |
2 |
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
TO (a; y) |
2 |
|
R1 |
|
|
|
R; |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
. oSTALXNYE PARY POLU^A@TSQ ANALOGI^NO. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
= |
|
(a; y); (a; z); (b; y); (b; z); (c; y) |
|
. |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
oTWET. R1 |
|
R; |
f |
g |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
zADA^A 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
wY^ISLITE ZNA^ENIE P7 ; 4 |
P(3; 2; 2) + A63 |
; A(4)6 ; 5 |
C72 ; C(8)3 . |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rE[ENIE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
wY^ISLQEM ZNA^ENIQ PERESTANOWOK, RAZME]ENIJ I SO^ETANIJ PO |
||||||||||||||||||||||||||||||||||||||||||||||||
FORMULAM, |
|
KOTORYE BYLI POLU^ENY W TRETXEJ GLAWE: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
P7 = 7! = 1 |
2 |
|
3 4 |
5 6 7 = 5040 ; |
|
P (3; 2; 2) = |
(3 + 2 + 2)! |
= 210 ; |
||||||||||||||||||||||||||||||||||||||||||
|
|
3! |
|
2! |
2! |
|||||||||||||||||||||||||||||||||||||||||||||
A3 |
= |
|
|
|
6! |
|
|
|
|
|
|
|
= 120; |
A6 |
|
= 46 = 4096; |
C |
2 |
|
= |
|
|
|
7! |
|
= 210 , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
6 |
|
|
(6 |
; |
3)! |
|
|
|
|
|
|
|
|
|
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
2! (7 ; 2)! |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
C |
3 |
|
= (8 + 3 ; 1)! = 120 . pODSTAWLQEM POLU^ENNYE ZNA^ENIQ W DAN- |
|||||||||||||||||||||||||||||||||||||||||||||||
(8) |
|
(8 |
; |
1)! |
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
6 |
|
|
|
|
|
|
2 |
|
3 |
|
|
|
||||||||||||||||||
NOE WYRAVENIE |
|
|
P7 ; 4 P (3; 3; 2) + A6 ; A(4) |
; 5 C7 ; C(8) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
= |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 5040 ; 4 210 + 120 ; 4096 ; 5 21 ; 120 = ;1 .
oTWET. P7 ; 4 P (3; 2; 2) + A36 ; A6(4) ; 5 C72 ; C(8)3 = ;1 .
zADA^A 6
nAJTI OB]IE FORMULY DLQ POSLEDOWATELXNOSTEJ an |
I bn , ESLI |
|||||||
a0 = 5 , b0 = 2 I |
an+1 = 6an ; 8bn; |
(1) |
||||||
|
|
|
|
|
bn+1 = 2an ; 4bn: |
(2) |
||
|
|
|
|
|
rE[ENIE |
|
||
iZ URAWNENIQ (1) WYRAVAEM bn I PODSTAWLQEM W URAWNENIE (2): |
||||||||
bn = |
1 |
(6an |
an+1); |
(3) |
||||
|
||||||||
8 |
|
|
|
|
|
|||
|
1 |
(6an+1 ; a;n+2) = 2an ; |
4 |
(6an ; an+1): |
(4) |
|||
8 |
8 |
|||||||
iZ (4) POSLE PREOBRAZOWANIJ POLU^AEM: an+2 ; 2an+1 ; 8an = 0: |TO REKURRENTNOE URAWNENIE QWLQETSQ LINEJNYM I ODNORODNYM,
PO\TOMU MOVNO PRIMENITX TEOREMU 1, SM. S. 41.
1.sOSTAWLQEM HARAKTERISTI^ESKOE URAWNENIE t2 ; 2t ; 8 = 0 , KOTOROE IMEET KORNI t1 = 4 I t2 = ;2 . kRATNOSTI k1 I k2 \TIH KORNEJ RAWNY 1, POSKOLXKU t2 ; 2t ; 8 = (t ; 4)1 (t + 2)1 .
2.fORMULA OB]EGO ^LENA DLQ an PO TEOREME 1 WYGLQDIT TAK:
an = P1(n)tn1 + P2(n)tn2 ; STEPENI MNOGO^LENOW P1(n) I P2(n) NA 1 MENX[E KRATNOSTEJ k1 I k2 . oTS@DA SLEDUET, ^TO \TI MNOGO^LENY
QWLQ@TSQ KONSTANTAMI, OBOZNA^IM IH ^EREZ A I B . tAKIM OBRAZOM: an = A 4n + B (;2)n .
3. dLQ NAHOVDENIQ A I B , NAPI[EM POLU^ENNU@ FORMULU DLQ
n = 0 I n = 1 , ESLI U^ESTX, ^TO a0 = 5 , A a1 = 6a0 ; 8b0 = 14 , TO POLU^AETSQ SISTEMA
A + B = 5; |
A = 4; |
||
4 |
A ; 2 |
B = 14; =) |
B = 1: |
4. tAKIM OBRAZOM, an = 4 |
4n + (;2)n . pODSTAWLQQ an W (3), |
||
NAJDEM |
1 |
6(4 4n + (;2)n) ;(4 4n+1 + (;2)n+1 = 4n + (;2)n . |
|
bn = 8 |
|||
oTWET |
|
n |
n |
n |
n |
|
|
4 + (;2) , bn = 4 + (;2) . |
|
||||||
|
. an = 4 |
|
|
||||
|
|
|
zADA^A 7 |
|
|
|
|
rE[ITX REKURRENTNOSTX an+2 + 10an+1 + 25an = 36 , |
(1) |
||||||
PRI USLOWII, ^TO a0 = 0 , a1 = ;4 . 69

rE[ENIE
uRAWNENIE (1) NE QWLQETSQ ODNORODNYM, T.K. EGO PRAWAQ ^ASTX RAWNA 36. ~TOBY IZBAWITXSQ OT NEODNORODNOSTI, ZAPI[EM (1) ZAME-
NIW n NA n + 1 : an+3 + 10an+2 + 25an+1 = 36 . |
(2) |
dALEE, IZ (2) PO^LENNO OTNIMEM (1) I POLU^IM |
|
an+3 + 9an+2 + 15an+1 ; 25an = 0 . |
|
rEKURRENTNOSTX STALA ODNORODNOJ I EE MOVNO RE[ATX PO OB]EJ |
|
SHEME, SOGLASNO TEOREME 1.
1. sOSTAWLQEM I RE[AEM HARAKTERISTI^ESKOE URAWNENIE
; |
|
) |
; |
|
|
n |
|
|
|
25 = 0 = |
t1 = 1; t2 = |
|
5 ; |
k1 = 1; k2 |
= 2 . |
||
2. pI[EM OB]U@ FORMULU an = A + (Bn + C)(;5) . |
|
|||||||
3. zNA^ENIQ A , B I C NAHODIM, RE[AQ SISTEMU |
|
|
||||||
a0 = A + C = 0; |
|
|
|
|
|
=) |
8 |
A = 1; |
8 a1 = A ; 5B ; 5C = ;4; |
; 10a1 ; 25a0 = 76: |
B = 2 |
||||||
< a2 = A + 50B + 25C = 36 |
|
< |
C = ;1: |
|||||
: oTWET. an = 1 + (2n ; 1)(;5)n . |
|
|
|
: |
|
|||
zADA^A 8
nAJDITE MATRICU SMEVNOSTI DLQ GRAFA G(X; ;) , GDE NABOR RE-
BER ; = ((x1; x2)?2; (x1; x3)?2; (x1; x4) ?3; (x2; x3); (x3; x4); (x2; x2))
I MNOVESTWO WER[IN X = fx1; x2; x3; x4g . rE[ENIE
nARISUEM DANNYJ GRAF G , SM. RIS. 37.
x2
x1
|
|
|
|
|
x3 |
|
A = 0 |
0 2 2 3 |
1 |
|
|
|
|
|
|
|
|||
|
|
b |
|
|
b |
||||
|
|
|
|
2 2 1 0 |
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
B |
2 1 0 1 |
C |
|
|
|
|
|
|
|
@ |
3 0 1 0 |
A |
|
|
b |
|
x4 |
b rIS. 37 |
||||
|
|
|
|
|
|||||
eGO MATRICA SMEVNOSTI QWLQETSQ KWADRATNOJ RAZMERA n n , GDE n { KOLI^ESTWO WER[IN GRAFA; W NA[EM SLU^AE n = 4 . |LEMENTAMI \TOJ MATRICY QWLQ@TSQ ^ISLA aij , POKAZYWA@]IE KOLI^ESTWO REBER, SOEDINQ@]IH WER[INY xi I xj . nAPRIMER, DLQ DANNOGO GRAFA a14 = 3 , a23 = 1 , a24 = 0 . kOLI^ESTWO PETELX U^ITYWAETSQ W DWOJNOM KOLI^ESTWE, PO\TOMU a22 = 2 . mATRICA SMEVNOSTI NEORIENTIROWANNOGO GRAFA QWLQETSQ SIMMETRI^ESKOJ, T.E. 8i; j (aij = aji) .
70
