
nasyrov_a_z_nasyrov_z_h_diskretnaya_matematika
.pdfNOE ZNA^ENIE ARGUMENTA, A TAKVE PRIMENQQ K NIM OPERACII SLOVENIQ, UMNOVENIQ, DIFFERENCIROWANIQ I INTEGRIROWANIQ.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
2k + 3 |
|
|
|
|
|
|
|
|
|
|
|
||||
pRIMER 4. nAJTI SUMMU |
S = 1 |
(k + 1)2k |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
k |
|
|
rE[ENIE. rAZLOVIM S NA DWE SUMMY: S1 |
|
= 2 |
X |
2 |
|
= 4 I |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2 = |
X |
|
|
|
|
|
|
|
|
. sUMMU |
S2 |
MOVNO NAJTI S POMO]X@ INTEGRI- |
||||||||||||||||||||||
|
(k + 1)2k |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ROWANIQ FORMULY DLQ A(t) |
W PRIMERE 1 W PREDELAH OT 0 DO 1=2 , |
|||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
POLU^IM |
|
|
(k + 1)2k+1 = ln 2 . uMNOVIW OBE ^ASTI \TOGO RAWENST- |
|||||||||||||||||||||||||||||||
|
k=0 |
|
||||||||||||||||||||||||||||||||
WA NA 2, NAJDEM, ^TO S2 = ln 4 . |
|
|
|
|
|
|
|
|
|
oTWET. S = 4 + ln 4 . |
||||||||||||||||||||||||
|
x7. lINEJNYE ODNORODNYE REKURRENTNOSTI |
|
||||||||||||||||||||||||||||||||
oPREDELENIE 1. pOSLEDOWATELXNOSTX |
|
(un)1 |
ZADANA LINEJNYM |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|||
ODNORODNYM REKURRENTNYM SOOTNO[ENIEM PORQDKA k , ESLI |
|
|||||||||||||||||||||||||||||||||
1) IZWESTNY ZNA^ENIQ u0; u1; : : : ; uk;1 |
|
| NA^ALXNYE DANNYE, |
||||||||||||||||||||||||||||||||
2) un |
= a1un |
; |
1 |
+ a2un |
; |
2 + : : : + akun |
; |
k , DLQ n > k , |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6= 0 . |
||||||
GDE a1; a2; : : : ; ak |
|
| IZWESTNYE KO\FFICIENTY, PRI^EM ak |
||||||||||||||||||||||||||||||||
pRIMER 1. pOSLEDOWATELXNOSTX fIBONA^^I ZADAETSQ TAK: |
|
|||||||||||||||||||||||||||||||||
u0 = u1 |
= 1 , un |
= un |
; |
1 + un |
; |
2 , DLQ |
|
n > 2 . nESKOLXKO PERWYH |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1; 1; 2; 3; 5; 8; 13; 21 . |
||||||||||||
^LENOW \TOJ POSLEDOWATELXNOSTI SLEDU@]IE: |
||||||||||||||||||||||||||||||||||
tEOREMA 1. pUSTX POSLEDOWATELXNOSTX (un)1 |
|
ZADANA REKUR- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
RENTNYM SOOTNO[ENIEM 2), TOGDA FORMULA OB]EGO ^LENA \TOJ PO- |
||||||||||||||||||||||||||||||||||
SLEDOWATELXNOSTI TAKOWA: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
un |
= P1(n)tn + P2(n)tn + : : : + Ps(n)tn , |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
GDE t1; t2; : : : ; ts |
|
| KORNI HARAKTERISTI^ESKOGO URAWNENIQ |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
f(t) = tk ; a1tk;1 ; a2tk;2 |
; |
|
: : : ; ak = 0 , |
|
|
|
|
|
||||||||||||||||||||||
A Pi(n) |
| MNOGO^LENY STEPENI ki |
; |
1 , |
GDE |
|
ki | KRATNOSTX ti |
||||||||||||||||||||||||||||
W KA^ESTWE KORNQ HARAKTERISTI^ESKOGO URAWNENIQ, |
i |
= 1; 2; : : : ; s , |
||||||||||||||||||||||||||||||||
PRI^EM k1 + k2 + : : : + ks |
= k . kO\FFICIENTY \TIH MNOGO^LENOW |
|||||||||||||||||||||||||||||||||
OPREDELQ@TSQ IZ NA^ALXNYH USLOWIJ 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
41

pRIMER 2. nAJTI OB]U@ FORMULU DLQ POSLEDOWATELXNOSTI fIBONA^^I.
|
rE[ENIE. pRIMENIM TEOREMU 1. wNA^ALE SOSTAWIM HARAKTERIS- |
||||||||||||||||||||||||||||||||||||||||
TI^ESKOE URAWNENIE t2 |
|
|
t |
|
|
1 = 0 I NAJDEM EGO KORNI t1 |
= |
|
1+p5 |
I |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
1;p5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
t2 |
= |
|
, KOTORYE IME@T KRATNOSTI k1 |
= k2 = 1 . zNA^IT, FORMU- |
|||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
LA DLQ un IMEET WID un = Atn +Btn |
. iSPOLXZUQ NA^ALXNYE DANNYE |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
1+p5 |
|
|
|
|
|
|
1;p5 |
|
|
|||||
u0 |
= u1 = 1 , OPREDELQEM KONSTANTY A = |
I |
B = |
|
; S |
||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
2p5 |
|
||||||||||||||||||||||||||||||||||||||||
U^ETOM \TOGO POLU^AEM OTWET |
|
|
|
|
|
|
|
|
|
|
|
|
; 2p5 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 + p |
|
! |
n+1 |
|
|
|
|
p |
|
! |
n+1 |
1. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
5 |
|
|
1 |
|
5 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
un = p |
|
|
|
|
|
|
2 |
|
|
|
; |
|
|
;2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
pRIMER 3. nAJTI@FORMULY DLQ POSLEDOWATELXNOSTEJA |
an I bn , |
|||||||||||||||||||||||||||||||||||||||
ESLI a0 = |
; |
1 , b0 = |
; |
1 |
I |
|
|
|
an+1 = 9an ; 12bn; |
|
|
|
|
|
|
(1) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bn+1 = 3an ; 3bn: |
|
|
|
|
|
|
(2) |
|||||||||||||||||||
|
rE[ENIE. iZ URAWNENIQ |
(1) WYRAVAEM |
|
bn I PODSTAWLQEM W URAW- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
bn = |
1 |
|
(9an |
|
|
an+1); |
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
NENIE (2): |
12 |
|
|
; a;n+2) = 3an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
(9an+1 |
; |
3 |
(9an ; an+1): |
(4) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
12 |
12 |
||||||||||||||||||||||||||||||||||
|
iZ (4) POSLE PREOBRAZOWANIJ POLU^AEM an+2 |
; 6an+1 + 9an = 0: |
|||||||||||||||||||||||||||||||||||||||
|
sOSTAWLQEM HARAKTERISTI^ESKOE URAWNENIE: |
|
t2 |
; |
6t + 9 = 0 = |
||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|TO URAWNENIE IMEET KORENX |
|
|
|
|
|
|
) |
|||||||||||||||||||||||||||
(t ; 3) = 0 . |
|
t1 = 3 , |
|
EGO KRATNOSTX |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
= (An + B)3 |
n |
|
|
|
|
|
|
|
|||||||||||||||||||||
k1 |
= 2 , TOGDA an = P1 |
(n)t |
|
|
. dLQ NAHOVDENIQ A I |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
B , NAPI[EM POLU^ENNU@ FORMULU DLQ n = 0 I n = 1 , ESLI U^ESTX,
|
|
|
; |
|
|
0 |
|
|
; |
|
|
|
|
|
|
|
|
|
^TO a0 = |
|
1 , A a1 |
= 9a0 |
|
|
12b0 |
= 3 , TO POLU^AETSQ SISTEMA: |
|
||||||||||
|
(A |
0 + B)3 = |
;1; |
|
= |
|
A = 2; |
|
|
|
|
|||||||
(A + B)31 = 3; |
|
|
|
) |
B = ;1: |
|
|
|
||||||||||
tAKIM OBRAZOM, an = (2n ; |
1)3n . pODSTAWLQQ |
an W (3), NAJDEM |
||||||||||||||||
bn = |
1 |
(9(2n |
; |
1)3n |
; |
(2n |
+ 1)3n+1) = (n |
; |
1)3n . |
n |
|
n |
||||||
|
|
|
|
|
|
|
||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, bn = (n ; 1)3 . |
||
|
|
|
|
|
|
|
|
|
|
oTWET |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
. an = (2n ; 1)3 |
|
|||||
uPRAVNENIQ PO KOMBINATORIKE
57. w MEN@ STOLOWOJ IMEETSQ 4 NAIMENOWANIQ ZAKUSKI, 2 | PERWOGO BL@DA, 3 | WTOROGO, 3 | TRETXEGO BL@DA I 2 WARIANTA DESERTA. sKOLXKIMI SPOSOBAMI MOVNO SOSTAWITX OBED, WYBIRAQ PO ODNOMU BL@DU KAVDOGO TIPA?
42
58.sKOLXKO DELITELEJ IMEET ^ISLO 37 54 ? nAJDITE SUMMU WSEH \TIH DELITELEJ.
59.wY^ISLITE ZNA^ENIE P6 ; A47 ; A5(3) .
60.sKOLXKIMI SPOSOBAMI 7 ^ELOWEK MOGUT WSTATX W O^EREDX?
61.sKOLXKIMI SPOSOBAMI MOVNO RASSADITX 6 GOSTEJ ZA KRUGLYM STOLOM? oDINAKOWYMI S^ITA@TSQ TE SPOSOBY, KOTORYE POLU^A@TSQ WRA]ENIEM.
o sKOLXKIMI SPOSOBAMI MOVNO RAKRASITX GRANI KUBA W [ESTX
62.
RAZNYH CWETOW, ESLI KAVDU@ GRANX KRASQT TOLXKO ODNIM CWETOM, A RAZLI^NYE GRANI | W RAZNYE CWETA?
o |
sKOLXKO IMEETSQ PERESTANOWOK ^ISEL |
1; 2; : : : ; n , W KOTORYH |
63. |
||
^ISLA 1 I 2 RASPOLOVENY RQDOM? |
|
|
64. |
sKOLXKO IMEETSQ TREHZNA^NYH ^ISEL, |
U KOTORYH WSE CIFRY |
RAZLI^NY?
o sKOLXKO IMEETSQ ^ETNYH PQTIZNA^NYH ^ISEL, U KOTORYH WSE
65.
CIFRY RAZLI^NY?
66.sKOLXKO TREHZNA^NYH ^ISEL MOVNO NAPISATX S POMO]X@ CIFR 1; 2; 3; 4 ? nAJDITE SUMMU WSEH \TIH ^ISEL.
67.sKOLXKIMI SPOSOBAMI MOVNO RASPREDELITX n RAZLI^NYH [A- ROW PO k RAZLI^NYM URNAM?
68.sKOLXKO IMEETSQ PODMNOVESTW U n -MNOVESTWA?
o sKOLXKO FUNKCIJ : , GDE = , = ? sKOLXKO
69. f A ! B jAj m jBj n
SREDI NIH IN_EKTIWNYH I BIEKTIWNYH FUNKCIJ?
o sKOLXKO RAZLI^NYH \LEMENTARNYH KON_@NKCIJ MOVNO OBRAZO-
70.
WATX IZ PEREMENNYH x1; x2; : : : ; xn ?
71. sKOLXKO RAZLI^NYH PERESTANOWOK MOVNO OBRAZOWATX IZ BUKW SLOWA "MATEMATIKA"?
o sKOLXKIMI SPOSOBAMI MOVNO PERESTAWLQTX BUKWY W SLOWE "KO-
72.
FEWARKA" TAK, ^TOBY GLASNYE I SOGLASNYE BUKWY ^EREDOWALISX?
43
73.iMEETSQ 5 QBLOK, 2 GRU[I, 3 APELXSINA. sKOLXKIMI SPOSOBAMI MOVNO DAWATX REBENKU PO ODNOMU FRUKTU W TE^ENIE 10 DNEJ?
74.sKOLXKIMI SPOSOBAMI MOGUT 3 RAZBOJNIKA PODELITX MEVDU SOBOJ 9 RAZLI^NYH PREDMETOW TAK, ^TOBY PERWOMU RAZBOJNIKU DOSTALOSX 4 PREDMETA, WTOROMU { 3, TRETXEMU { 2 PREDMETA?
75.s KAKIM KO\FFICIENTOM WHODIT ab2c3 W RAZLOVENIE MNOGO^LE-
NA (a + b + c + d)6 ?
76.nAJDITE KO\FFICIENT PRI x8 U MNOGO^LENA (1 ; x2 + x3)9 .
77. nAJDITE KO\FFICIENT PRI t5 W RAZLOVENII (1 + 2t ; 3t2)8 .
78.
o nAJDITE NAIBOLX[IJ KO\FFICIENT W RAZLOVENII MNOGO^LENA
(1 + x)10 .
79. nAPI[ITE RAZLOVENIE MNOGO^LENA (x1 + x2 + : : : + xk)2 .
o |
nAPI[ITE RAZLOVENIE MNOGO^LENA (x1 + x2 + : : : + xk)3 . |
80. |
1 |
|
2 |
|
|
|
k |
81. dOKAVITE, ^TO Cnk = n |
|
n ; 1 |
|
: : : |
|
n ; k + 1 . |
82.wY^ISLITE C1412 + C53 ; P (3; 0;2) .
83.dOKAVITE, ^TO Cnk + 2Cnk+1 + Cnk+2 = Cnk+2+2 .
o |
nAJDITE k , ESLI C |
k |
= C |
k+4 |
. |
84. |
10 |
10 |
|||
|
|
|
|
85.sKOLXKO IMEETSQ ^ETYREHZNA^NYH ^ISEL, U KOTORYH CIFRY SLEWA NAPRAWO WOZRASTA@T?
86.sKOLXKO WSEGO POLU^ITSQ PARALLELOGRAMMOW, ESLI SERI@ IZ ^E- TYREH PARALLELXNYH PRQMYH PERESE^X SERIEJ IZ PQTI PARALLELXNYH PRQMYH?
87. dOKAVITE, ^TO Ck = |
n |
|
n + 1 |
|
: : : |
|
n + k ; 1 . nAJDITE C1 , |
||
|
(n) |
1 |
2 |
|
k |
(100) |
|||
|
|
|
|
|
|
|
|
||
C2 |
, C3 . |
|
|
|
|
|
|
|
|
(100) |
(10) |
|
|
|
|
|
|
|
|
88.w KIOSKE IME@TSQ OTKRYTKI 10 WIDOW. sKOLXKIMI SPOSOBAMI MOVNO WYBRATX 12 OTKRYTOK?
89.sKOLXKIMI SPOSOBAMI MOVNO RASPREDELITX k ODINAKOWYH [A- ROW PO n RAZLI^NYM URNAM?
44

o sKOLXKIMI SPOSOBAMI MOVNO RAZMESTITX W RQD BELYH I
90. p q
^ERNYH [ARA TAK, ^TOBY NIKAKIE DWA ^ERNYH [ARA NE RASPOLAGALISX RQDOM?
91. sKOLXKO RE[ENIJ IMEET URAWNENIE x1 + x2 + x3 = 10 W NATURALXNYH ^ISLAH?
o sKOLXKIMI SPOSOBAMI MOVNO RASPREDELITX ODINAKOWYH [A-
92. k
ROW PO n RAZLI^NYM URNAM TAK, ^TOBY NE BYLO PUSTYH URN?
93.nAJDITE KOLI^ESTWO SLAGAEMYH POSLE PRIWEDENIQ PODOBNYH ^LENOW W RAZLOVENII MNOGO^LENA (x1 + x2 + x3 + x4)5 .
94.nAJDITE KOLI^ESTWO NATURALXNYH ^ISEL, NE PREWOSHODQ]IH 1000, KOTORYE NE DELQTSQ NI NA 3, NI NA 5, NI NA 7.
o nAJDITE KOLI^ESTWO NATURALXNYH ^ISEL, NE PREWOSHODQ]IH
95.
1000, KOTORYE NE DELQTSQ NI NA 6, NI NA 10, NI NA 15.
96.sKOLXKO ^ISEL OT 0 DO 999 NE IME@T NI ODNOJ CIFRY 1 W SWOEJ DESQTI^NOJ ZAPISI?
97.sKOLXKIMI SPOSOBAMI MOVNO POLOVITX 5 RAZLI^NYH [AROW W 3 RAZLI^NYH Q]IKA TAK, ^TOBY NE BYLO PUSTYH Q]IKOW?
98.sKOLXKO IMEETSQ LATINSKIH PRQMOUGOLXNIKOW 3 4 , S PERWOJ STROKOJ (1 2 3 4) I WTOROJ STROKOJ (4 3 2 1) ?
o sKOLXKO IMEETSQ LATINSKIH PRQMOUGOLXNIKOW 3 5 , S PERWOJ
99.
STROKOJ (1 2 3 4 5) I WTOROJ STROKOJ (2 1 4 5 3) ?
100. nAJDITE A(t) DLQ POSLEDOWATELXNOSTI (uk)1 , ESLI
k=0
uk = 1 PRI 0 6 k 6 n I uk = 0 PRI k > n .
101. nAJDITE E(t) DLQ POSLEDOWATELXNOSTI
A) P0; P1 ; : : : ; Pk; : : : , B) A0n; A1n; : : : ; Ann; 0; 0; : : : .
102. nAJDITE A(t) I E(t) DLQ POSLEDOWATELXNOSTI
A0(n); A1(n) ; : : : ; A(kn); : : : .
103. nAJDITE A( 12 ) DLQ POSLEDOWATELXNOSTI uk = C(kn) .
104. nAJDITE A(t) DLQ POSLEDOWATELXNOSTI (uk)1 , ESLI
k=0
45
A) uk = k , B) uk = k2 .
onAJDITE ( ) DLQ POSLEDOWATELXNOSTI
105.A t
onAJDITE ( ) DLQ POSLEDOWATELXNOSTI
106.E t
A) uk = k , |
B) uk = k2 . |
|
|
||||
nAJDITE SLEDU@]IE SUMMY (107 { 112). |
|||||||
107. |
C0 |
+ 1 C1 |
+ 1 C |
2 + : : : + |
1 |
Cn . |
|
n + 1 |
|||||||
|
n |
2 n |
3 |
n |
n |
||
o |
Cn0 |
; Cn1 + Cn2 + : : : + (;1)nCnn . |
|||||
108. |
|||||||
o |
C1 |
+ 2C2 |
+ 3C3 + : : : + nCn . |
|
|||
109. |
|
||||||
|
n |
n |
n |
n |
|
||
uk = k(k ; 1) .
(uk)1k=0 , ESLI
110. |
1 |
|
|
|
|
|
k |
k |
. |
|
|
(2k + 3)C(n)t |
|
||||||
|
k=0 |
|
|
|
|
|
|
|
|
|
P |
|
|
2k |
|
|
|
||
111. |
1 |
|
|
|
|
||||
k=1 |
(k + 2)k! . |
|
|
||||||
|
|
|
|||||||
|
X |
|
|
|
|
|
|
|
|
112. |
1 |
|
|
tk |
|
|
|
|
|
k=4 |
k |
; |
3 . |
|
|
|
|||
|
|
|
|
||||||
|
X |
|
|
|
|
|
|
||
rE[ITE SLEDU@]IE REKURRENTNOSTI (113 { 116). |
|||||||||
113. |
u1 = 2 , u2 = 3 ; un = 2un;1 ; un;2 . |
||||||||
114. |
a1 = 14 , b1 = ;6 ; an+1 = 3an + bn , bn+1 = ;an + bn . |
||||||||
o |
a0 = 1 , b0 = 0 ; an+1 = an + bn+1 , bn+1 = an ; 2bn . |
||||||||
115. |
|||||||||
116. |
a1 = b1 = 0 ; an+1 = bn + 10 , bn+1 = an + 6 . |
||||||||
46
g l a w a 4
grafy
x1. pONQTIE GRAFA. mATRICA SMEVNOSTI I EE SWOJSTWA
oPREDELENIE 1. gRAFOM G NAZYWAETSQ PARA (X; ;) , W KOTOROJ
X = fx1 ; x2; : : : ; xng { MNOVESTWO WER[IN, A ; = (g1; g2; : : : ; gm) {
NABOR REBER GRAFA, PRI^EM KAVDOE REBRO gi = (xk; xl) | NEUPORQDO^ENNAQ PARA WER[IN, NAZYWAEMYH KONCAMI REBRA gi . oDNO I TO VE REBRO MOVET WHODITX W NABOR ; NESKOLXKO RAZ, T.E. DOPUSKA@TSQ KRATNYE REBRA.
rEBRO WIDA (xk; xk) NAZYWAETSQ PETLEJ. gRAF BEZ PETELX I KRATNYH REBER NAZYWAETSQ PROSTYM.
|
pRIMER |
1. nA RIS. 18 PRIWEDE- |
x2 |
|
b x1 b |
|
|||
|
|
|
|
|
|||||
NA GEOMETRI^ESKAQ REALIZACIQ GRAFA |
|
|
|
|
|||||
G(X; ;) , GDE X = fx1; x2; x3; x4g , A |
|
x3 |
|
|
x4 |
|
|||
|
|
b rIS. 18b |
|
||||||
; = ((x1; x1); (x1; x2) ? 2; (x2; x3)) . |
|
|
|
||||||
|
oPREDELENIE 2. oRIENTIROWANNYM GRAFOM |
;! |
NAZYWAETSQ PA- |
||||||
|
G |
||||||||
RA |
(X; ;) , |
W KOTOROJ |
X = fx1 ; x2 |
; : : : ; xng |
{ |
MNOVESTWO WER[IN |
|||
|
|
|
|
|
|||||
GRAFA, A ; |
= (g1 ; g2; : : : ; gm) { NABOR DUG, |
PRI^EM KAVDAQ DUGA |
|||||||
gi =< xk; xl > | UPORQDO^ENNAQ PARA WER[IN, xk |
{ NA^ALO, A xl |
{ |
|||||||
KONEC DUGI gi . oDNA I TA VE DUGA MOVET WSTRE^ATXSQ W NABORE |
; |
||||||||
NESKOLXKO RAZ. |
|
|
|
|
|
|
|
||
w DANNOM POSOBII BUDUT RASSMATRIWATXSQ TOLXKO NEORIENTIROWANNYE GRAFY. mNOGIE SWOJSTWA NEORIENTIROWANNYH GRAFOW PERENOSQTSQ NA ORIENTIROWANNYJ SLU^AJ. wMESTE S TEM, ORIENTIROWANNYE GRAFY OBLADA@T CELYM RQDOM WAVNYH HARAKTERISTIK, SWOJSTWENNYH TOLXKO IM, POZNAKOMITXSQ SO SWOJSTWAMI ORIENTIROWANNYH GRAFOW MOVNO W PRIWEDENNOJ LITERATURE.
47
oPREDELENIE 3. sTEPENX@ WER[INY x GRAFA G(X; ;) NAZYWAETSQ KOLI^ESTWO REBER IZ ; , IME@]IH x SWOIM KONCOM, PRI \TOM PETLQ U^ITYWAETSQ DWAVDY. oBOZNA^AETSQ STEPENX TAK: deg x .
eSLI deg x = 0 , TO WER[INA x NAZYWAETSQ IZOLIROWANNOJ; ESLI deg x = 1 , TO x | TUPIKOWAQ (KONCEWAQ, WISQ^AQ) WER[INA.
wER[INY xk I xl | SMEVNYE, ESLI REBRO (xk; xl) 2 ; , REBRA NAZYWA@TSQ SMEVNYMI, ESLI ONI IME@T OB]U@ WER[INU.
tEOREMA 1 ("O RUKOPOVATIQH"). sUMMA STEPENEJ WSEH WER[IN
n
P deg xi = 2m .
i=1
dOKAZATELXSTWO. pRI SUMMIROWANII STEPENEJ WSEH WER[IN L@- BOE REBRO U^ITYWAETSQ W KAVDOM IZ SWOIH DWUH KONCOW, PO\TOMU POLU^AETSQ UDWOENNOE ^ISLO REBER.
eSTX RAZNYE SPOSOBY PREDSTAWLENIQ GRAFOW W |wm. eSLI GRAF IMEET NEBOLX[OE ^ISLO REBER, TO UDOBNO ZADATX GRAF S POMO]X@ SPISKOW SMEVNYH WER[IN: DLQ KAVDOJ WER[INY x UKAZYWA@T WSE WER[INY, SMEVNYE S x . tAKVE, MOVNO ZADAWATX GRAF S POMO]X@ MATRICY SMEVNOSTI.
oPREDELENIE 4. mATRICEJ SMEVNOSTI GRAFA G NAZYWAETSQ MATRICA A = (aij) RAZMERA n n , W KOTOROJ \LEMENT aij RAWEN KOLI- ^ESTWU REBER, SOEDINQ@]IH WER[INY xi I xj . pETLI, PRI \TOM, U^ITYWA@TSQ DWAVDY.
sWOJSTWO 1. mATRICA SMEVNOSTI QWLQETSQ SIMMETRI^NOJ, T.E.
AT = A .
sWOJSTWO 2. sUMMA \LEMENTOW i -TOJ STROKI MATRICY RAWNQETSQ deg xi .
sWOJSTWO 3. sUMMA WSEH \LEMENTOW MATRICY SMEVNOSTI RAWNA UDWOENNOMU ^ISLU REBER GRAFA.
x2. pODGRAF. ~ASTI^NYJ, NULEWOJ, POLNYJ,
DOPOLNITELXNYJ GRAF. sOEDINENIE GRAFOW
oPREDELENIE 1. gRAF G0(X0; ;0) NAZYWAETSQ PODGRAFOM GRAFA
G(X; ;) , ESLI X0 X , A ;0 ; .
oPREDELENIE 2. gRAF, POLU^AEMYJ IZ G(X; ;) UDALENIEM NEKOTORYH REBER BEZ IZMENENIQ MNOVESTWA WER[IN X , NAZYWAETSQ
48
^ASTI^NYM DLQ GRAFA G .
oPREDELENIE 3. gRAF, WSE n WER[IN KOTOROGO QWLQ@TSQ IZOLIROWANNYMI, NAZYWAETSQ NULEWYM I OBOZNA^AETSQ On .
o^EWIDNO, ^TO NULEWOJ GRAF QWLQETSQ ^ASTI^NYM DLQ L@BOGO GRAFA S TEM VE MNOVESTWOM WER[IN.
oPREDELENIE 4. pROSTOJ GRAF, L@BYE DWE WER[INY KOTOROGO QWLQ@TSQ SMEVNYMI, NAZYWAETSQ POLNYM. pOLNYJ GRAF S
NAMI OBOZNA^AETSQ Kn ILI Fn .
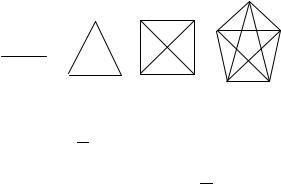
nA RIS. 19 DANY IZOBRAVENIQ GRAFOW K2 , K3 , K4 , K5 . w MATRICE SMEVNOSTI POLNOGO GRAFA WSE \LEMENTY RAWNY 1, KROME \LEMENTOW, RASPOLOVENNYH NA GLAWNOJ DIAGONALI I RAWNYH 0. o^EWIDNO, ^TO L@BOJ PROSTOJ GRAF QWLQETSQ ^ASTI^NYM DLQ POLNOGO GRAFA S TEM VE MNOVESTWOM WER[IN.
|
c |
c |
c |
c |
c |
c |
c |
c c |
c c |
c |
c |
|
c |
|
rIS. 19 |
|
|
|
|
|
oPREDELENIE 5. dOPOLNITELXNYM K PROSTOMU GRAFU Q(X; ;) NA-
ZYWAETSQ PROSTOJ GRAF Q(X; ;) TAKOJ, ^TO ;\; = ? , A G(X; ;[;)
{ POLNYJ.
tAKIM OBRAZOM, DOPOLNITELXNYJ GRAF G IMEET TE REBRA IZ POLNOGO GRAFA, KOTORYH NET W GRAFE G .
|
|
oPREDELENIE 6. sOEDINENIEM NEPERESEKA@]IHSQ GRAFOW G(X; ;) |
|||
I G0(X0; ;0) , X \ X0 |
= ? , NAZYWAETSQ GRAF, OBOZNA^AEMYJ G + G0 |
||||
I RAWNYJ |
(X [ X0; ; |
[ ;0 [ f(x; x0)j x 2 X; x0 2 X0g) . |
|||
|
|
|
|||
|
|
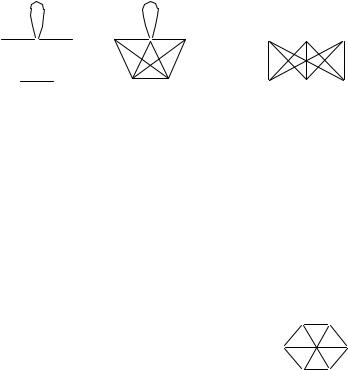
nA RIS. 20 IZOBRAVENY GRAFY G , G0 I RQDOM PRIWEDENO IZOB- |
|||
RAVENIE GRAFA G + G0 . |
|||||
|
|
sOEDINENIE O |
+ O00 OBOZNA^AETSQ ^EREZ Km;n , WER[INY IZ |
||
|
|
|
m0 |
|
n |
O |
m0 |
BUDEM USLOWNO NAZYWATX "DOMIKAMI", A IZ O00 { "KOLODCAMI"; |
|||
|
|
|
|
n |
|
NA RIS. 21 DANO IZOBRAVENIE GRAFA K3;3 .
49
G |
c |
c |
c |
c |
c |
c |
x1 bx2 bx3 |
|
b |
|||
G0 |
|
c |
c |
c |
c |
|
y1 |
b |
y2 |
by3 |
|
b |
|
|
|
rIS. 20 |
|
|
|
rIS. 21 |
|
|
|||
x3. iZOMORFIZM GRAFOW. rEALIZACIQ GRAFOW W |
R |
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
oPREDELENIE 1. gRAF G(X; ;) NAZYWAETSQ IZOMORFNYM GRAFU |
||||||||||||
G0(X0; ;0) , OBOZNA^AETSQ |
G ' G0 , ESLI SU]ESTWUET BIEKTIWNOE OTO- |
|||||||||||
BRAVENIE |
f : X |
! X0 TAKOE, ^TO a(xi; xj) = a(f(xi); f(xj)) , T.E. |
||||||||||
KOLI^ESTWO REBER, SOEDINQ@]IH L@BYE WER[INY xi |
I xj W GRAFE |
|||||||||||
G , RAWNO KOLI^ESTWU REBER, SOEDINQ@]IH SOOTWETSTWU@]IE WER- |
||||||||||||
[INY W GRAFE G0 . |
|
|
|
|
|
|
|
|
|
|||
pRIMER 1. gRAF, IZOBRAVENNYJ NA RIS. |
|
z5 |
z4 |
|
|
|||||||
21 IZOMORFEN GRAFU, IZOBRAVENIE KOTORO- |
|
|
|
|||||||||
|
|
|
b |
b |
|
|||||||
GO DANO NA RIS. 22. bIEKTIWNOE OTOBRAVE- |
|
|
|
|
||||||||
z6 |
b |
|
z3 b |
|||||||||
NIE f MOVNO ZADATX, NAPRIMER, TAKIM OB- |
|
|||||||||||
RAZOM: f(x1) = z1 , f(x2) = z3 , f(x3) = z5 , |
|
z1 |
z2 |
b |
|
|||||||
f(x4) = z2 , |
f(x5) = z4 , f(x6) = z6 . |
|
|
rIS. b22 |
|
|||||||
pRIMER 2. dOKAZATX, |
^TO GRAFY |
G1 I |
G2 |
NA RISUNKE 23 NE |
||||||||
IZOMORFNY. |
|
|
|
|
|
|
|
|
|
|
|
|
rE[ENIE. dLQ NEIZOMORFNOSTI GRAFOW DOSTATO^NO UKAZATX HARAKTERISTIKU, PO KOTOROJ ONI OTLI^A@TSQ DRUG OT DRUGA. w DANNOM SLU^AE GRAF G1 IMEET CIKL, SOSTOQ]IJ TOLXKO IZ WER[IN STEPENI 3, A GRAF G2 TAKOGO CIKLA NE IMEET. zNA^IT, \TI GRAFY NE IZOMORFNY.
oPREDELENIE 2. gOWORQT, ^TO GRAF G DOPUSKAET REALIZACI@ W PROSTRANSTWE Rn , ESLI EGO WER[INAM MOVNO SOPOSTAWITX TO^KI IZ Rn , A REBRAM SOPOSTAWITX NEPRERYWNYE KRIWYE, SOEDINQ@]IE SOOTWETSTWU@]IE TO^KI, TAK ^TOBY \TI KRIWYE NE IMELI WNUTRENNIH TO^EK PERESE^ENIQ S DRUGIMI KRIWYMI. rEALIZACIEJ GRAFA W Rn NAZYWAETSQ IZOBRAVENIE, POLU^ENNOE PRI \TOM SOPOSTAWLENII.
50
