
Решения
.docЗадача 2.
Имеются изделия четырех сортов.
![]() первого сорта .
первого сорта .
![]() второго сорта .
второго сорта .
![]() третьего сорта.
третьего сорта.
![]() четвертого сорта.
четвертого сорта.
Для контроля на удачу выбирается 6 изделий . Определить вероятность того что среди них окажется
![]() первосортное
первосортное
![]() второсортных
второсортных
![]() третьего сорта
третьего сорта
![]() четвертого сорта.
четвертого сорта.
Решение:
Для решения используется гипергеометрическое распределение.
Суммарное число изделий
![]()
Суммарное число изделий в выборке
![]()
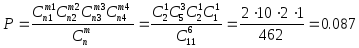
Задача 5.
В отрезке единичной длины на удачу
появляется точка К. Определить вероятность
того что расстояние от точки до обоих
концов отрезка превосходит величину
![]() .
.
Решение:
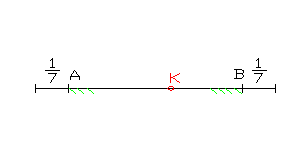
![]() весь отрезок единичной длины
весь отрезок единичной длины
![]() при условии равновероятного попадания
в любую точку.
при условии равновероятного попадания
в любую точку.
Задача 8.
В двух партиях 81 и 37 % доброкачественных деталей соответственно . На удачу выбирается по одному изделию из каждой партии . Какова вероятность обнаружить среди них .
1. хотя бы одно бракованное.
Решение.
Пусть
![]() - событие выбора качественного изделия
из первой партии.
- событие выбора качественного изделия
из первой партии.
![]() - событие выбора качественного изделия
из второй партии.
- событие выбора качественного изделия
из второй партии.
Тогда искомое событие
![]() где
где
![]() - не
- не
![]()
![]()
![]()
![]()
![]()
Вероятность события
![]()
2. Два бракованных.
Решение:
Искомое событие
![]()
Вероятность события
![]()
3. Одно доброкачественное и одно бракованное.
Решение:
Искомое событие
![]()
Вероятность события
![]()
Задача 11.
Задание:
Урна содержит 9 занумерованных шаров с номерами от 1 до 9 . Шары извлекаются по одному без возвращения . определить вероятность событий:
 .
Номера шаров в порядке поступления
образуют последовательность 1, 2, 3 ...
.
Номера шаров в порядке поступления
образуют последовательность 1, 2, 3 ...
Решение:
Вероятность правильного выбора первого
шара
![]() второго шара
второго шара
![]() и так далее так как в урне всегда
присутствует только один шар с нужным
номером . Общая вероятность равна
и так далее так как в урне всегда
присутствует только один шар с нужным
номером . Общая вероятность равна
![]()
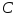 .
нет ни одного совпадения номера шара с
порядком извлечения.
.
нет ни одного совпадения номера шара с
порядком извлечения.
Решение:
Рассмотрим вероятность события когда шар извлекается в соответствии с номером.
Так при первом выборе вероятность выбрать шар с нужным номером (нужный это соответствующий порядку извлечения) равна
![]()
где
![]() -число
шаров в совокупности. Так как выбирается
один шар из
-число
шаров в совокупности. Так как выбирается
один шар из
![]() .
.
Но при выборе второго шара нужно учесть вероятность того что нужный шар мог быть взят при первом выборе и суммарная вероятность для шара быть не выбранным в прошлый раз и выбранным в этот равна:
![]()
соответственно для третьего раза:
![]()
и так далее .Соответственно для любого номера шара вероятность быть не выбранным равна
![]()
Полная вероятность для урны с
![]() шарами:
шарами:
![]()
При
![]() равном 9:
равном 9:
![]()
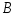 .
Хотя бы один раз совпадает номер шара
и порядковый номер извлечения (событие
B).
.
Хотя бы один раз совпадает номер шара
и порядковый номер извлечения (событие
B).
Решение:
Противоположным является событие в
котором размещение не содержит элементов
которые находятся на своих местах , а
это также 1 вариант в множестве размещений
![]()
![]()
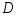 .
Найти предельные значения вероятностей
при числе шаров
.
Найти предельные значения вероятностей
при числе шаров
Решение:
при
![]()
![]()
![]()
![]()
Задача 14.
Задание.
В альбоме из
![]() марок
марок
![]() чистых марок и
чистых марок и
![]() гашеных . Из них на удачу выбирается 2
марки (любых) и подвергаются спец гашению
после чего возвращаются обратно. Затем
вновь наудачу извлекается 3 марки .
Определить вероятность того что все 3
марки чистые.
гашеных . Из них на удачу выбирается 2
марки (любых) и подвергаются спец гашению
после чего возвращаются обратно. Затем
вновь наудачу извлекается 3 марки .
Определить вероятность того что все 3
марки чистые.
Решение:
Пусть выбор для спец гашения одной
чистой марки это событие
![]()
двух чистых марок это событие
![]()
ни одной чистой марки это событие
![]()
Пусть выбор 3 чистых марок при наличии
![]() чистых марок это событие
чистых марок это событие
![]()
Тогда событие выбора 3 чистых марок
![]() равно :
равно :
![]()
![]()
для вычисления вероятностей используется гипергеометрическое распределение :
при первом выборе:
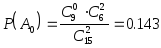

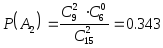
при втором выборе:
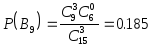
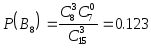
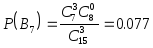
![]()
Задача 17.
Задание:
Вероятность выигрыша в лотерею равна 0.4 .Куплено 13 билетов .Найти наиболее вероятное число выигрышных билетов и соответствующую вероятность.
Решение:
Допустим имеется
![]() билетов и из них
билетов и из них
![]() выигрышных. Всего существует
выигрышных. Всего существует
![]() размещений этих билетов .Вероятность
обнаружить какое либо из этих размещений
равна
размещений этих билетов .Вероятность
обнаружить какое либо из этих размещений
равна
![]() где
где
![]() -вероятность
позитивного исхода а
-вероятность
позитивного исхода а
![]() -вероятность
негативного исхода. и полная вероятность
обнаружить
-вероятность
негативного исхода. и полная вероятность
обнаружить
![]() выигрышных билета равна в пачке из
выигрышных билета равна в пачке из
![]() билетов
билетов
![]()
отсюда можно вычислить вероятности:
![]()
![]()
![]()
Задача 20.
Задание:
Вероятность наступления некоторого
события в серии из
![]() независимых экспериментов равна 0.6
.Определить вероятность того что число
наступлений события
независимых экспериментов равна 0.6
.Определить вероятность того что число
наступлений события
![]() удовлетворяет неравенствам:
удовлетворяет неравенствам:
Решение:
 n
от 40 до 50.
n
от 40 до 50.
В прошлой задаче была получена формула
для нахождения вероятности обнаружить
![]() позитивных результата в наборе из
позитивных результата в наборе из
![]() проб. Здесь
проб. Здесь
![]() .
Вероятность зафиксировать от 40 до 50
событий равна:
.
Вероятность зафиксировать от 40 до 50
событий равна:
![]()
 n
до 40
n
до 40
![]()
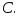 n
до 50
n
до 50
![]()
Задача 23.
Задание:
По данному закону распределения случайной
величины найти характеристическую
функцию
![]() математическое
ожидание
математическое
ожидание
![]() и дисперсию
и дисперсию
![]() случайной величины
случайной величины
![]()
Решение:
1. Математическое ожидание.
По определению:
![]()
2. Дисперсия.
По определению:
![]()
![]()
3. Характеристическая функция.
![]()
Задача 26.
Задание:
Случайная величина
![]() имеет плотность распределения
имеет плотность распределения
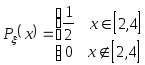 другая случайная величина связана с
другая случайная величина связана с
![]() функциональной
зависимостью
функциональной
зависимостью
![]() . Определить математическое ожидание
. Определить математическое ожидание
![]() и дисперсию
и дисперсию
![]() случайной величины
случайной величины
Решение:
1. Математическое ожидание.
По определению:
![]()
2. Дисперсия.
По определению:
![]()
Задача 29.
Задание:
По данной плотности
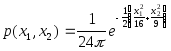 распределения двумерной случайной
величины найти плотность распределения
случайной величины однозначно связанной
с соотношениями
распределения двумерной случайной
величины найти плотность распределения
случайной величины однозначно связанной
с соотношениями
![]()
![]()
Решение:
Пусть искомое распределение
![]() тогда должно выполнятся условие:
тогда должно выполнятся условие:
![]()
то есть:
![]()
где
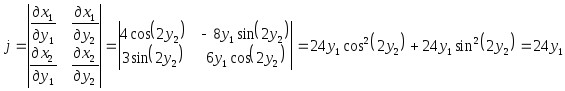
тогда:
![]()
что вполне аналогично ковариантной замене координат.
Задача 32.
Условие:
Случайная величина
![]() может с одинаковой вероятностью принимать
одно из двух значений :
может с одинаковой вероятностью принимать
одно из двух значений :
![]() или
или
![]() .Выяснить
удовлетворяет ли последовательность
попарно независимых случайных величин
.Выяснить
удовлетворяет ли последовательность
попарно независимых случайных величин
![]() закону больших чисел.
закону больших чисел.
Решение:
1) для
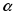 равного
равного
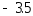 .
.
![]()
математическое ожидание
![]()
следовательно необходимо доказать:
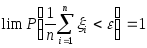
будем рассматривать функцию
![]() как случайную величину
как случайную величину
![]() .
По условию каждое значение принимается
с равной вероятностью. В пределе величину
можно рассматривать как непрерывную.
Величина очевидно удовлетворяет условию:
.
По условию каждое значение принимается
с равной вероятностью. В пределе величину
можно рассматривать как непрерывную.
Величина очевидно удовлетворяет условию:
![]()
обе эти ограничивающие последовательности
сходятся к 0 следовательно в пределе
![]() может принимать только значение 0 с
вероятностью 1. То есть система
удовлетворяет закону больших чисел.
может принимать только значение 0 с
вероятностью 1. То есть система
удовлетворяет закону больших чисел.
1) для
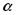 равного
равного
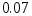 .
.
![]()
математическое ожидание
![]()
следовательно необходимо доказать:

будем рассматривать функцию
![]() как случайную величину
как случайную величину
![]() .
По условию каждое значение принимается
с равной вероятностью. В пределе величину
можно рассматривать как непрерывную.
Величина очевидно удовлетворяет условию:
.
По условию каждое значение принимается
с равной вероятностью. В пределе величину
можно рассматривать как непрерывную.
Величина очевидно удовлетворяет условию:
![]()
обе эти ограничивающие последовательности
расходятся следовательно в пределе
![]() распределена по бесконечному интервалу
и принимает значение 0 с вероятностью
0.
распределена по бесконечному интервалу
и принимает значение 0 с вероятностью
0.
Задача 35.
Условие:
Известно что случайная величина
распределена по биномиальному закону
![]() неизвестным считается параметр
неизвестным считается параметр
![]() используя метод наибольшего правдоподобия
найти по реализации выборки
используя метод наибольшего правдоподобия
найти по реализации выборки
![]() значение оценки
значение оценки
![]() неизвестного параметра
неизвестного параметра
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решение:
функция правдоподобия имеет вид:
![]()
где
![]()
критическая точка уравнения правдоподобия:
![]()
