ТерВер

100

P X 2 10 0,8 2 0,2 3 0,0512; P X 3 10 0,8 3 0,2 2 0,2048;

P X 4 5 0,8 4 0,2 0,4096; P X 5 1 0,8 5 0,32768.

Таким образом, ряд распределения имеет вид:

Математическое ожидание и дисперсию находим по формулам для биномиального распределения:

M X np 5 0,8 4 , D X npq 5 0,8 0,2 0,8 .

2.Стрелок проводит по мишени три выстрела. Вероятность попадания

вмишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий. Найти среднее значение числа попаданий.

Решение. Число попаданий является дискретной случайной величиной X. Каждому значению xn случайной величины X отвечает определенная

вероятность pn .

Закон распределения дискретной случайной величины в данном случае можно задать рядом распределения. В данной задаче случайная величина X принимает значения 0, 1, 2, 3. По формуле Бернулли

pn (k) P X k Cnk pk qn k ,

найдем вероятности возможных значений случайной величины:

p3 0 0,7 3 0,343,

p3 1 C31 0,3 0,7 2 0,441, p3 2 C32 0,3 2 0,7 0,189, p3 3 0,3 3 0,027.

101

Расположив значения случайной величины X в возрастающем порядке, получим ряд распределения:

n1

означает вероятность того, что случайная величина X примет хотя бы одно значение из числа возможных, а это событие достоверное, поэтому

4

Pn 1.

n 1

Таким образом, случайная величина X имеет биномиальное распределение. Математическое ожидание такой случайной величины равно

M X np 3 0,3 0,9.

3. Страховая компания заключает однотипные договоры, причем, страховая премия (сумма, выплачиваемая страхуемым при заключении договора) составляет 4 тысячи рублей. При наступлении страхового случая компания должна выплатить 20000 рублей. Известно, что страховой случай наступает в 4 % случаев. Фирме удалось застраховать 200 клиентов. Необходимо определить:

а) каков средний доход фирмы и среднеквадратическое отклонение фирмы?

б) какова вероятность того, что доход фирмы будет находиться в пределах от 710000 до 750000 рублей?

Решение. Обозначим через X случайную величину, равную количеству клиентов, которым страховая компания будет делать выплаты по страховому случаю. Так как страховой случай наступает в 4 % случаев, то вероятность того, что он наступит при работе с одним конкретным клиентом, равна 0,04. Поэтому случайная величина X имеет биномиальный закон распределения с параметрами n 200 и p 0,04 , то есть X B200;0,04 .

Обозначим через Y случайную величину, равную доходу фирмы. Согласно условию задачи, случайная величина Y связана с X следующим образом:

Y 200 4000 20000 X .

102

а) Воспользуемся свойствами математического ожидания и дисперсии для нахождения M Y и D Y :

M Y M 800000 20000 X 800000 20000 M X ,

D Y D 800000 20000 X 200002 D X 4 108 D X .

Для биномиального закона распределения известно, что

M X n p 200 0,04 8, D X np 1 p 200 0,04 0,96 7,68 .

Получаем,

M Y 800000 20000 8 640000, D Y 4 108 7,68 3072 106 .

Таким образом, среднее квадратическое отклонение

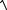
3072 106 55426 рублей.

б) Вероятность вычисляем по формуле

P a X b F b F a .

Получим

P 710000 Y 750000 P 2,5 X 4,5 P X 3 P X 4

C2003 0,04 3 0,96 200 3 C2004 0,04 4 0,96 200 4 0,0825.

Заметим, что при большом числе испытаний вычисления проводить очень сложно, поэтому для нахождения вероятностей P X 3 и P X 4 можно использовать приближенную формулу Пуассона (2.17)

Pn k k e k!

где np 200 0,04 8 . Получим,

103

Как мы видим, вероятность оказалась очень мала.

4. Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины Х – числа выпадений четного суммарного числа очков на двух игральных костях.

Решение. Введем в рассмотрение случайное событие

А = {на двух костях при одном броске выпало в сумме четное число очков}.

Используя классическое определение вероятности найдем

Р(А)= mn ,

где n – число всевозможных исходов испытания находим по правилу умножения:

n = 6∙6 = 36,

m – число благоприятствующих событию А исходов – равно m 3 6 18 . Таким образом, вероятность успеха в одном испытании равна

p P A 12 .

Задача решается с применением схемы испытаний Бернулли. Одним испытанием здесь будет бросание двух игральных костей один раз. Число таких испытаний n = 2. Случайная величина Х принимает значения 0, 1, 2 с вероятностями

Искомое биноминальное распределение случайной величины Х можно представить в виде ряда распределения:

104

5. Определить математическое ожидание случайной величины Х – числа бросков монеты до первого появления герба.

Решение. Здесь мы имеем геометрическое распределение. Ряд распределения имеет вид:

Тогда М ( Х ) 0,51 2.

6. Автобусы некоторого маршрута идут с интервалом 5 минут. Найти вероятность того, что пришедшему на остановку пассажиру придется ожидать автобуса не более 2 минут.

Решение. Время ожидания является случайной величиной, равномерно распределенной на отрезке [0, 5]. Тогда, согласно (5.5)

И по (5.7) P(0 x 2) 52 0, 4.

7. Пусть дана случайная величина X N1, 4 . Вычислить вероятность

P 0 X 3 .

Решение. Здесь a 1, 2. Согласно формуле (5.13) имеем

0 1 0 0,5 0,34 0,19 0,53.

Значения функции 0 x смотрим в таблице.

8. Волжский автомобильный завод запускает в производство новый двигатель. Конструкторы двигателя считают, что среднее число км пробега для автомобиля с новым двигателем составляет 160000 км со стандартным

0 1,5 0 0,5 0,4531.

Теперь найдем границы, в которых будет находиться текущая цена акции. По правилу трех сигм текущая цена акции будет находиться в интервале a 3 ; a 3 15 3 0,2; 15 3 0,2 14,4; 15,6 .

Задачи для самостоятельного решения

1.Сдача экзамена по математике проводится до получения положительного результата. Шансы сдать экзамен остаются неизменными и составляют 20 %. Найти математическое ожидание числа попыток сдачи экзамена.

2.Написать биномиальный закон распределения дискретной случайной величины – числа появлений «герба» при двух бросаниях монеты.

106

3.В партии из 10 деталей – 8 стандартных. Наудачу отобраны 2 детали. Составить закон распределения числа стандартных деталей среди отобранных.

4.Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины – числа выпадений четного числа очков на двух игральных костях.

5.Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятности того, что в пути будет повреждено изделий: а) ровно 3 изделия; б) менее трех; в) более трех; г) хотя бы одно.

6.Из двух орудий поочередно ведется стрельба по цели до первого попадания одним из орудий. Вероятность попадания в цель первым орудием равна 0,3, вторым – 0,7. Начинает стрельбу первое орудие. Составить законы распределения дискретных случайных величин – числа израсходованных снарядов соответственно первым и вторым орудием.

7.Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) менее двух; в) более двух; г) хотя бы одну.

8.На станцию обслуживания заявки поступают случайно в

соответствии с распределением Пуассона при 2 . Мощность станции позволяет обслуживать не более двух заявок в единицу времени. Найти вероятность того, что в течение данной единицы времени: а) станция не справится с потоком заявок и образуется очередь; б) станция обслуживания будет простаивать или работать не на полную мощность; в) на станции обслуживания очередь не образуется.

9.Случайная точка A имеет в круге радиуса R равномерное распределение. Найти математическое ожидание и дисперсию расстояния точки до центра круга.

10.Стержень длиной 24 см ломают на две части; будем считать, что точка излома распределена равномерно по всей длине стержня. Чему равна средняя длина большей части стержня?

11.Отрезок длиной 12 см случайным образом разрезается на 2 части. Точка разреза равномерно распределена на всей длине отрезка. Чему равна средняя длина малой части отрезка?

12.Случайная величина равномерно распределена на отрезке 2,6 .

Выписать плотность распределения. Найти функцию распределения. Найти вероятность попадания случайной величины на отрезок 2,5 и на отрезок

5,7 .

13. Время безотказной работы ЭВМ распределено по показательному закону с параметром = 0,05 (отказа в час), т.е. имеет функцию плотности

Решение определенной задачи требует безотказной работы машины в течение 15 минут. Если за время решения задачи произошел сбой, то ошибка обнаруживается только по окончании решения, и задача решается заново. Найти: а) вероятность того, что за время решения задачи не произойдет ни одного сбоя; б) среднее время, за которое будет решена задача.

14. Длительность времени безотказной работы элемента имеет показательное распределение F t 1 e0,03t . Найти вероятность того, что

за время длительностью t 100 ч: а) элемент откажет; б) элемент не откажет. 15. Испытывают два независимо работающих элемента. Длительность времени безотказной работы первого имеет показательное распределение

откажут; в) только один элемент откажет; г) хотя бы один элемент откажет.

16.Найти дисперсию и среднее квадратическое отклонение

17.Найти дисперсию и среднее квадратическое отклонение

18. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 10 и 2. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале 12, 14 .

19. Автомат штампует детали. Контролируется длина детали X , которая распределена нормально с математическим ожиданием, равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.

Указание. Из равенства P 32 X 68 1 найти .

20. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением 10 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.

Указание. Так как измерения без систематических ошибок, считаем математическое ожидание равным нулю.

симметричного относительно математического ожидания, в который с вероятностью 0,9973 попадет X в результате испытания.

Указание. Использовать «правило трех сигм».

22.Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от проектного не превышает 10 мм.

Случайные отклонения контролируемого размера от проектного подчинены нормальному закону со средним квадратическим отклонением 5 мм и математическим ожиданием a 0. Сколько процентов годных деталей производит автомат?

23.В рекламных целях торговая фирма вкладывает в каждую десятую единицу товара денежный приз размером 1 тыс. руб. Составить закон распределения случайной величины – размера выигрыша при пяти сделанных покупках.

Ответы. 1) 5;

2)

P Y k 0,553 0,21k 1; 7) а) 0,224; б) 0,1992; в) 0,5768; г) 0,95; 8) а) 0,32;

значениями 0, 1, 2, 3, 4, 5.

Контрольные вопросы

1. Перечислите основные виды дискретных законов распределения. Как они задаются?

2. Перечислите основные виды непрерывных законов распределения. Как они задаются?

3. По какой формуле вычисляется вероятность попадания случайной величины в интервал , ?

4.Как вычисляются математическое ожидание и дисперсия случайной величины, распределенной по биномиальному закону?

5.Если случайная величина распределена по закону Пуассона, то чему равны ее математическое ожидание и дисперсия?

6.Приведите формулы для вычисления математического ожидания и дисперсии равномерно распределенной случайной величины.

7.Приведите формулы для вычисления математического ожидания и дисперсии нормально распределенной случайной величины.

8.Чему равно математическое ожидание случайной величины, распределенной по показательному закону?

9.Сформулируйте «правило трех сигм».

10.Дайте определение функции надежности.