
ТерВер
.pdf90
|
|
|
т1 |
|
|
т1 |
|
|
||
|
(т 1) |
|
|
е |
|
|
е |
( 1). |
||
|
|
|
|
|
|
|||||
|
|
(т 1)! |
т1 (т 1)! |
|
|
|||||
т1 |
|
|
||||||||
Тогда D X 2 2 .
Таким образом, обнаружено интересное свойство распределения Пуассона: математическое ожидание равно дисперсии (и равно единственному параметру , определяющему распределение).
Основные виды непрерывных распределений
Равномерный закон распределения.
Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение, т.е.
c, при x [a, b], f (x)
0, при x [a, b].
Найдем значение с, которое принимает f(x) при x [a,b]. Из условия
|
|
b |
b |
|
1 |
|
|
нормировки следует, что |
|
f (x)dx cdx c(b a) 1, откуда |
c |
. |
|||
|
|||||||
b a |
|||||||
|
|
a |
a |
|
|
||
|
|
|
|
|
|||
Таким образом, |
|
|
|
|
|
||
|
1 |
, при x [a, b], |
|
|
|
||
|
|
|
|
|
|
||
|
a |
|
|
|
|||
f (x) b |
|
|
(5.5) |
||||
|
|
при x [a, b]. |
|
|
|
||
0, |
|
|
|
|
|||
График плотности f (x) для равномерного распределения непрерывной
случайной величины X изображен на рис. 5.1.
Функцию распределения непрерывной случайной величины X, распределенной по равномерному закону достаточно легко найти и она имеет следующий вид:
|
|
0, |
|
при x a, |
|
|
|
|
x |
|
a |
|
|
|
|
|
|
x |
|
|
|
||
F (x) |
f (t)dt |
|
|
, при a x |
b, |
(5.6) |
|
|
a |
||||||
|
|
b |
при x b. |
|
|||
|
|
1, |
|
|
|||
|
|
|
|
|
|
|
|

91
График F(x) изображен на рис. 5.2.
f(х)
1/(b – a)
O |
a |
b |
x |
Рис. 5.1
 F(х)
F(х)
1
O |
a |
|
|
|
b |
x |
|
|
Рис. 5.2 |
|
|
||
Если случайная |
величина |
X распределена |
равномерно на отрезке |
|||
a,b , тогда пишут X Ua, b (либо X Ra,b ). |
|
|||||
Вероятность попадания равномерно распределенной случайной |
||||||
величины на интервал , a b равна |
|
|||||
|
|
|
1 |
|
|
|
P x |
|
|
||||
|
dx b a . |
(5.7) |
||||
b a |
||||||
|
|
|
|
|
|
|
92
Определим математическое ожидание и дисперсию равномерно распределенной случайной величины X. Согласно формуле (3.20),
|
|
|
a |
|
|
|
b |
|
x |
|
|
|
|
|
|
|
|
|
|
a b |
|
|
|
|
|
|||||||
M ( X ) |
|
x 0dx |
|
|
dx |
x 0dx |
. |
|
|
(5.8) |
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
b a |
|
|
b |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Согласно формуле (3.13), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
b |
|
|
|
a b |
2 |
|
|
dx |
|
|
1 |
|
|
|
1 |
|
|
a b |
3 |
|
b |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
D( X ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
a |
|
|
|
|
2 |
|
b a |
|
|
b a 3 |
|
|
|
2 |
|
|
a |
|
|||||||||||||
|
1 |
|
|
|
(b a)3 |
|
|
(a b)3 |
|
|
|
(b a)2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
(5.9) |
||||||
3(b a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
8 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нормальный закон распределения.
Нормальный закон (закон Гаусса) играет исключительную роль в теории вероятностей. Главная особенность закона Гаусса состоит в том, что он является предельным законом, к которому приближаются при определенных условиях, другие законы распределения. Нормальный закон наиболее часто встречается на практике.
Множество явлений в практической жизни можно описать с помощью модели нормального распределения, например, распределение высоты деревьев, веса людей, дневной температуры и т.д. Нормальное распределение используется и для решения проблем в экономической жизни. Это, например, распределение числа дневных продаж в магазине, числа посетителей магазина в неделю, числа работников в некоторой отрасли, объем выпуска продукции на предприятии и т.д.
Нормальное распределение иногда называют законом ошибок. Случайный эффект различных величин и обсуждаемых источников определяют как «ошибки». Например, отклонения в размерах деталей от номинального объясняется многими причинами, каждая из которых влияет на размер детали; так что отклонение, которое фактически регистрируется при измерениях, является суммой большого числа отклонений, ошибок.
12 ноября 1733 г. Абрахам де Муавр (1667–1754), родившийся во Франции, опубликовал маленький памфлет о нормальном распределении и распространил его среди близких друзей. Памфлет был вскоре забыт. И лишь столетие спустя маркиз де Лаплас (1749–1827) и К. Ф. Гаусс (1777–1855) одновременно объявили об открытии ими закона нормального распределения независимо от работ Муавра. И с этих пор нормальное распределение часто называют законом Лапласа – Гаусса.
93
Непрерывная случайная величина X распределена по нормальному закону с параметрами a и > 0, если ее плотность распределения имеет вид
|
|
|
|
|
|
|
(x a)2 |
|
|
f (x) |
|
1 |
|
|
e |
22 |
, x R. |
(5.10) |
|
|
|
|
|
|
|
||||
|
2 |
|
|
Обозначается X Na, 2 .
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Выясним, какой вид имеет эта кривая, для чего исследуем функцию (5.10).
1) Область определения этой функции есть интервал , .
2) |
f x 0 при |
|
|
любом |
x (следовательно, |
весь график |
расположен |
||||||||||||||||||||||||
выше оси Ох). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) |
lim |
f (x) 0, |
|
то есть ось Ох служит горизонтальной асимптотой |
|||||||||||||||||||||||||||
|
|x| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
графика при x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
(x a)2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
при x a ; f |
|
||||||||||||
4) |
Производная |
f (x) |
3 |
|
|
|
|
e |
|
|
|
|
|
|
0 |
(x) 0 при |
|||||||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
x a , f |
|
при x a . Следовательно, a, |
|
|
|
|
|
– точка максимума. |
|||||||||||||||||||||||
(x) 0 |
|
|
|
|
|
||||||||||||||||||||||||||
|
f x a f a x , |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||
5) |
то |
|
|
есть |
|
график |
симметричен относительно |
||||||||||||||||||||||||
прямой x a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6) Производная второго порядка |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(x a)2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
(x a)2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
1 |
|
|
|
|
|
|
0 при x a , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
f |
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то есть точки |
a , |
|
|
|
|
|
|
|
являются точками перегиба. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
2 e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
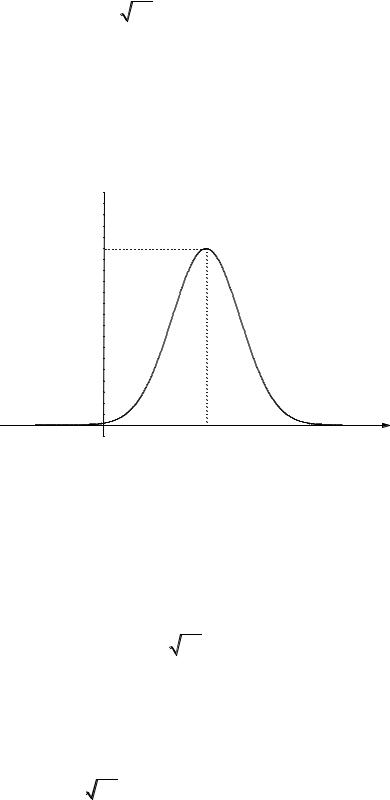
График функции (5.10) изображен на рис. 5.3. |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
Функция |
распределения |
|
F (x) f (t)dt |
непрерывной |
случайной |
||||||||||||||||||||||||||
величины X Na, 2 имеет вид:
94
|
|
|
|
|
x |
|
(t a)2 |
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
22 |
|
|
||||
F (x) |
|
|
|
dt . |
(5.11) |
||||
|
|
|
|
e |
|
||||
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Этот интеграл не выражается через элементарные функции. Поэтому для вычисления значений F x приходится пользоваться таблицами. Они
составлены для случая, когда a 0, а 1.
Если a = 0 и 1, то нормальное распределение с такими параметрами называется стандартным или нормированным.
 f(х)
f(х)
1/ (2 )1/2
|
|
a |
x |
|
|
|
Рис. 5.3 |
|
|
Функция |
распределения |
случайной |
величины |
X N0,1, |
распределенной по стандартному закону, имеет вид
(x)
и называется функцией Лапласа.
равенство x 1 x .
1 |
|
x |
e |
t2 |
||
|
|
|
||||
|
|
2 |
dt |
|||
|
|
|
||||
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что для этой нее выполняется
|
|
|
|
|
|
|
x e |
t2 |
|
||
|
|
|
(x) |
1 |
|
|
dt (x) |
1 |
|
||
Функция |
0 |
|
2 |
называется нормированной |
|||||||
|
|
|
|
||||||||
|
|
|
|
2 |
2 |
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
функцией Лапласа. Нормированная функция Лапласа является нечетной, т.е.
0 x 0 x .
Значения этой функции можно найти по таблице в приложении.

95
Функцию распределения для произвольных параметров (5.11) можно
выразить через функцию Лапласа, если сделать замену:
|
|
|
|
|
|
|
t a 2 |
|
|
|
|
x a |
|
t2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
2 |
2 |
|
1 |
|
|
|
x a |
|
|||||
F (х) |
|
|
|
e |
|
|
dx |
|
|
|
е |
2 dt |
|
|
, т.е. |
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t x a , тогда
x a |
|
1 |
|
x a |
|
|||||
F (x) |
|
|
|
|
0 |
|
|
. |
(5.12) |
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
||||
На языке случайных величин этот факт можно сформулировать следующим образом: если случайная величина X Na, 2 , то случайная
величина Y X a N0,1.
Для вычисления математического ожидания и дисперсии нормально распределенной случайной величины воспользуемся интегралом Пуассона
|
e |
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 dz |
|
|
2 . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x a)2 |
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
z2 |
||||||||
|
M X |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
z a e |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
xe |
|
|
|
dx |
z |
|
|
|
|
|
|
|
|
|
|
|
2 dz |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
ze |
|
|
a |
|
|
|
e |
|
|
|
a |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 dz |
|
|
2 |
dz 0 |
|
|
|
|
2 a |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(первое слагаемое равно 0, так как подынтегральная функция нечетна, а пределы интегрирования симметричны относительно нуля). Аналогично находим
|
|
|
|
|
|
|
|
|
(x a)2 |
|
|
2 |
|
z2 |
|
|
z2 |
|
|
||||
D X |
|
1 |
|
x a |
2 |
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
z ze |
|
|
|
||||||||||||
|
|
|
|
|
e |
|
dx |
|
|
|
|
|
2 dz u z,dv ze |
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

96
|
2 |
|
|
|
|
z |
2 |
|
|
|
|
z |
2 |
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
z e |
|
|
|
|
e |
|
|
|
|
0 |
2 2 . |
|||||||||
|
|
|
|
|
2 |
|
|
|
2 dz |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, параметры нормального распределения а и равны соответственно математическому ожиданию и среднему квадратическому отклонению исследуемой случайной величины.
Вероятность попадания случайной величины X Na, 2 на заданный участок , вычисляется по формуле
P X
|
a |
|
a |
|
||
f t dt F F |
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
a |
0 |
|
a |
(5.13) |
||
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
||
На практике часто приходиться вычислять вероятность попадания нормально распределенной случайной величины в интервал, симметричный относительно центра рассеяния a:
P |
|
X a |
|
P a X a 0 |
|
|
0 |
|
|
|
2 0 |
|
|
(5.14) |
|||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. Случайная величина Х имеет нормальное распределение с параметрами а = 3, σ = 2. Найти вероятность того, что она примет значение из интервала (4, 8).
Решение. Воспользуемся формулой (5.13):
|
8 3 |
|
|
4 3 |
|
|
||
P 4 x 8 F 8 F 4 |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|||||
|
|
|
|
|
|
|
||
2,5 0,5 0,9938 0,6915 0,3023.
Найдем вероятность того, что нормально распределенная случайная величина Х примет значение из интервала a 3 , a 3 :
P а 3 X а 3 3 3 0,9986 0,0014 0,9973.
97
Следовательно, вероятность того, что значение случайной величины окажется вне этого интервала, равна 0,0027, то есть составляет 0,27 % и может считаться пренебрежимо малой. Таким образом, на практике можно считать, что все возможные значения нормально распределенной случайной величины лежат в интервале (а – 3σ, а + 3σ).
Полученный результат позволяет сформулировать следующее правило,
которое называется правилом «трех сигм»: если случайная величина распределена нормально, то модуль ее отклонения от х = а не превосходит
3σ.
Показательный закон распределения.
Непрерывная случайная величина X имеет показательный закон распределения, если ее плотность вероятности имеет вид
|
x |
, при x 0, |
|
e |
|
(5.15) |
|
f (x) |
|
при x 0, |
|
0, |
|
|
|
|
|
|
|
где 0 параметр распределения. В этом случае пишем X E .
В отличие от нормального распределения, показательный закон определяется только одним параметром . В этом его преимущество, так как обычно параметры распределения заранее не известны и их приходится оценивать приближенно.
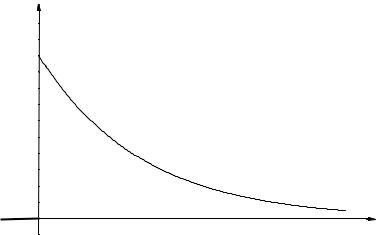
График плотности f(x) приведен на рис. 5.4.
f(х)
O |
x |
|
Рис. 5.4
Найдем функцию распределения показательного закона:
|
|
|
98 |
|
|
x |
0 |
|
x |
|
|
F (x) f (t)dt 0 dt e tdt 1 e x. |
|
||||
|
|
|
0 |
|
|
Следовательно, |
|
|
|
|
|
|
e |
x |
, |
при x 0, |
|
1 |
|
(5.16) |
|||
F (x) |
|
|
|
при x 0. |
|
0, |
|
|
|
||
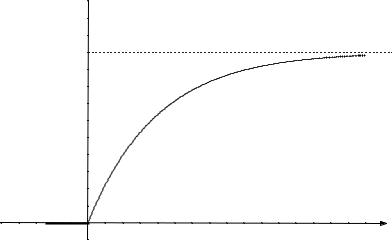
График F(x) представлен на рис. 5.5.
 F(х)
F(х)
1
O |
x |
Рис. 5.5
Теперь можно найти вероятность попадания распределенной случайной величины в интервал (а, b):
P a X b e a e b .
Значения функции e x можно найти из таблиц. Математическое ожидание M(X) и дисперсия D(X)
распределения равны
показательно
(5.17)
показательного
M ( X ) |
1 |
, |
D( X ) |
1 |
. |
(5.18) |
|
|
|||||
|
|
|
2 |
|
||
Пусть элемент (то есть некоторое устройство) |
начинает работать в |
|||||
момент времени t0 = 0 и должен проработать в течение периода времени t. Обозначим за Т непрерывную случайную величину – время безотказной
99
работы элемента, тогда функция F(t) = p(T < t) определяет вероятность отказа за время t. Следовательно, вероятность безотказной работы за это же время равна
(5.19)
Эта функция называется функцией надежности.
Часто длительность безотказной работы элемента имеет показательное распределение, то есть
F t 1 e t .
Следовательно, функция надежности в этом случае имеет вид:
R t 1 F t 1 1 e t e t .
Показательным законом надежности называют функцию надежности,
определяемую равенством
R t e t , |
(5.20) |
где λ – интенсивность отказов.
Пример. Пусть время безотказной работы элемента распределено по показательному закону с плотностью распределения f t 0,1e0,1t при
t 0 . Найти вероятность того, что элемент проработает безотказно в течение 10 часов.
Решение. Так как 0,1, то по (5.20) получаем
R 10 e0,110 e1 0,368.
Примеры решения задач к главе 5
1. Составить ряд распределения случайной величины Х – числа попаданий при 5 выстрелах, если вероятность попадания при одном выстреле равна 0,8. Найти ее математическое ожидание и дисперсию.
Решение. Это будет биномиальное распределение. Вычислим вероятности по формуле (5.2):
P X 0 1 0,2 5 0,00032; P X 1 5 0,8 0,2 4 0,0064;
