LR2

Теория электрических и радиотехнических цепей

ЛАБОРАТОРНАЯ РАБОТА № 3

ИССЛЕДОВАНИЕ ДИСКРЕТИЗАЦИИ НЕПРЕРЫВНЫХ СИГНАЛОВ

ЦЕЛЬ И СОДЕРЖАНИЕ

Цель – изучение основ дискретизации и восстановления непрерывных сигналов по теореме В. А. Котельникова.

Содержание лабораторной работы:

-изучение теоретического обоснования и примеров дискретизации непрерывных сигналов в соответствии с теоремой В. А. Котельникова;

-выполнение индивидуального задания и оформление отчета;

-защита отчета по лабораторной работе.

Теоретическое обоснование

В настоящее время все радиоэлектронные системы, включая системы телефонии, радиовещания и телевидения, переходят на цифровой режим работы. В основе преобразования различных непрерывных (аналоговых) сигналов для их обработки в цифровой форме лежит процедура дискретизации. В связи с этим вводятся следующие понятия:

-непрерывный (аналоговый) сигнал – это сигнал x t , который является непрерывным как во времени, так и по значению;

-дискретный сигнал x k tд , где k = 0, ±1, ±2, ±3, … – это сигнал, кото-

рый получается в результате дискретизации значений аналогового сигнала x t ; - дискретизация – это определение значений аналогового сигнала в дис-

кретные моменты времени.

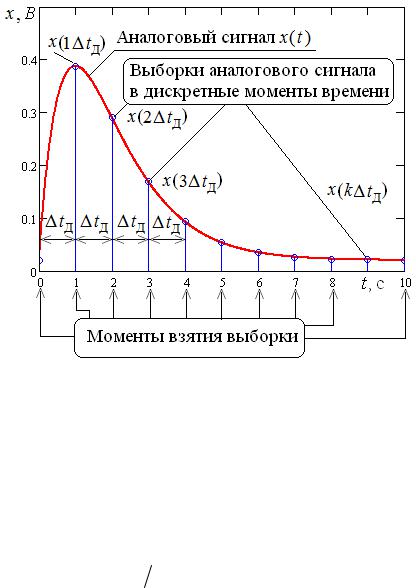
Пример аналогового сигнала, подвергшегося дискретизации, показан на рисунке 2.1. Отметим, что после дискретизации, представленной на рисунке 2.1, аналоговый сигнал представлен только в дискретные моменты времени, причем значения сигнала в эти моменты равны соответствующим значениям исходного

аналогового сигнала.

1

Теория электрических и радиотехнических цепей

Рисунок 2.1 – Пример аналогового сигнала, подвергшегося дискретизации

Как правило, при дискретизации отсчеты аналогового сигнала берутся через равные промежутки времени tд (рисунок 2.1), называемые периодом дискрети-

зации (или интервалом, шагом дискретизации – sample time).

Величина, обратная периоду дискретизации, называется частотой дискретизации (sampling frequency): fД 1 tД . Соответствующая ей круговая частота оп-

ределяется следующим образом: Д 2 tД .

Таким образом, дискретный сигнал непрерывен по амплитуде, но определяется только в дискретных точках во времени.

Ясно, что в общем случае представление аналогового сигнала набором дискретных отсчетов приводит к потере информации, так как остается неизвестным поведении сигнала в промежутках между отсчетами (выборками). Однако существует класс аналоговых сигналов, для которых такой потери информации не происходит и которые могут быть точно восстановлены по значениям своих дискретных отсчетов. К этому классу относятся сигналы, подчиняющиеся теореме, сформулированной в 1933 году выдающимся отечественным ученым Владимиром Александровичем Котельниковым: «Любой сигнал s t , спектр которого не со-

2

Теория электрических и радиотехнических цепей

Формирование непрерывного сигнала по его дискретным отсчетам поясняет рисунок 2.2. Пунктиром показаны графики отдельных слагаемых формулы (2.3), сплошной линией – восстановленный аналоговый сигнал.

Рисунок 2.2 – Восстановление аналогового сигнала по его дискретным отсчетам

Рисунок 2.2 наглядно демонстрирует главное свойство сигнала с ограниченным спектром – его бесконечность во времени. Хотя отличны от нуля лишь несколько отсчетов показанного сигнала, аналоговый сигнал оказывается бесконечно колеблющимся между нулевыми отсчетами (на рисунке это отсчеты с номерами –2, –1, 4, 5, 6) его значения отличны от нуля. Эти колебания нигде не заканчиваются, хотя их амплитуда стремится к нулю.

Таким образом, для полного восстановления непрерывного сигнала x t по

набору его дискретных отсчетов x k tд необходимо просуммировать беско-

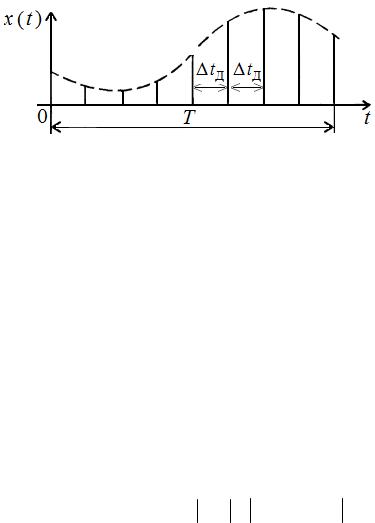
нечное множество членов ряда (2.3). Однако если функция с ограниченным спектром x(t) рассматривается на конечном интервале времени T (рисунок 2.3), то точное разложение (2.3) можно заменить следующим приближённым разложением:

4

Теория электрических и радиотехнических цепей

Рисунок 2.3 – Функция с ограниченным спектром x(t) рассматривается на конечном интервале времени T

Конечное число дискретных отсчетов n, ед., укладывающихся на конечном интервале времени T, рассчитывается по формуле

Параметр B 2 fBT в формуле (2.6) называют базой сигнала. Очевидно, что погрешность восстановления сигнала при ограничении числа его отсчётов n будет тем больше, чем меньшее число слагаемых учитывается при суммировании в формуле (2.5).

Оценим качественно погрешность (t) xε t x t . Поскольку все сла-

гаемые ряда (2.5) обращаются при t i tд в нуль во всех точках, за исключением,

слагаемого с номером k = i, то в этих сечениях значения совпадают с x(t), т. е. погрешность (k tд) равна нулю; очевидно, погрешность достигнет наибольшей величины внутри промежутка между отсчётами. Кроме того, величина погрешности нарастает к краям рассматриваемого интервала времени T (рисунок 2.4). Таким образом, приходим к выводу, что первой причиной погрешности восстановления функции с ограниченным спектром x(t по совокупности её дискретных от-

5

Теория электрических и радиотехнических цепей

счетов) определенных на конечном интервале времени T (формула (2.5)) является то, что число таких дискретных отсчетов конечно.

Рисунок 2.4 – Изменение погрешности (t) xε t x t в пределах интервала времени T

Другая причина погрешностей обусловлена тем, что спектры реальных непрерывных (аналоговых) сигналов не обращаются в нуль за пределами верхней граничной частоты аналогового сигнала fB, Гц. Хотя основная энергия сигналов расположена на частотах от –fB до fB, некоторая часть энергии приходится на частоты выше граничной. С учетом этого, относительная среднеквадратическая погрешность восстановления исходного непрерывного сигнала x t по набору его

дискретных отсчетов x k tд определяется соотношением

где E – та часть энергии, которая оказывается за пределами полосы частот от

–fB до fB и не учитывается при восстановлении сигнала, В2с; Е – полная энергия сигнала x(t), В2с;

x2 – квадрат нормы сигнала x(t), В2с.

Таким образом, при заданной погрешности (2.7) можно определить необходимую граничную частоту fB, а, следовательно, и интервалы между отсчётами

6

Теория электрических и радиотехнических цепей

грешности за счёт неучитываемой части спектра сигнала будут тем больше, чем медленнее убывает спектр сигнала за пределами граничной частоты fB.

Третьей причиной погрешностей восстановления функции с ограниченным спектром x(t по совокупности её дискретных отсчетов) определенных на конечном интервале времени T являются неидеальные характеристики фильтра нижних частот (ФНЧ), формирующего функции k t , образующие базис Котельникова на приемной стороне канала связи. Как известно из лекционного курса, колебания, имеющие форму базисной функции Котельникова вида (2.4), можно получить на выходе идеального ФНЧ с граничной частотой fB при действии на его входе дельта-импульса δ(t). Амплитудно-частотная характеристика (АЧХ) идеального ФНЧ равномерна (рисунок 2.5):

где H – комплексная передаточная функция идеального ФНЧ.

Рисунок 2.5 – Идеальные и реальные частотные характеристики ФНЧ, формирующего функции k t , образующие базис Котельникова на приемной стороне канала связи

В свою очередь, фазочастотная характеристика (ФЧХ) – линейна (рисунок

2.5):

Arg H t ,

7

Как известно из курса теории электрических и радиотехнических цепей, импульсная характеристика фильтра hδ(t) может быть определена на основе обратного интегрального преобразования Фурье от комплексной передаточной функции H фильтра:

hδ t 21 H e j tdt .

Для рассматриваемого случая идеального ФНЧ импульсная характеристика фильтра hδ(t) определяется соотношением вида

рисунке 2.5), используемых на приемной стороне канала связи, отличаются от идеальных (сплошные кривые на рисунке 2.5). Это приводит к отклонениям реальных функций k t (пунктирная кривая на рисунке 2.6), образующих базис Котельникова на приемной стороне канала связи, от идеальных (сплошная кривая на рисунке 2.6) и, как следствие, к появлению дополнительных погрешностей восстановления сигнала x(t) по набору его дискретных отсчетов x k tд , k = 0, 1, 2, … , n – 1, определенных на конечном интервале времени T.

Рисунок 2.6 – Идеальные и реальные базисные функции Котельникова

Таким образом, для применения теоремы В. А. Котельникова на практике необходимо определить верхнюю граничную частота аналогового сигнала fB, Гц.

8

Теория электрических и радиотехнических цепей

Методика определения верхней граничной частоты сигнала fB с использованием двух подходов (информационного и энергетического) была рассмотрена на первом лабораторном занятии «Исследования числовых параметров сигналов».

Воспользуемся результатами примера, рассмотренного на первом лабораторном занятии, связанными с анализом числовых параметров сигнала представляющего собой прямоугольный импульс высотой A и длительностью τ и рассмотрим методику его дискретизации и восстановления по теореме В. А. Котельникова.

АППАРАТУРА И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ

Аппаратура. Для выполнения лабораторной работы необходим персональный компьютер со следующими характеристиками: процессор Pentium/Celeron с тактовой частотой 300 МГц и выше, оперативная память не менее 128 Мбайт и более, свободное дисковое пространство не менее 100 MB Мбайт, устройство для чтения компакт-дисков, монитор типа Super VGA (число цветов 256).

Программное обеспечение. Для выполнения лабораторной работы необходима операционная система WINDOWS 2000/ XP Professional, библиотека Microsoft .NET Framework версии 1.1 или выше, программа MathCAD 10 и выше.

УКАЗАНИЯ ПО ТЕХНИКЕ БЕЗОПАСНОСТИ

При выполнении лабораторной работы запрещается:

-самостоятельно производить ремонт персонального компьютера, а также установку и удаление имеющегося программного обеспечения;

-нарушать общепринятые правила техники безопасности при работе с электрооборудованием, в частности, касаться электрических розеток металлическими предметами и т.д.;

-принимать пищу, напитки и сорить на рабочем месте пользователя персонального компьютера.

9

Теория электрических и радиотехнических цепей

Вслучае неисправности персонального компьютера необходимо немед-

ленно сообщить об этом обслуживающему персоналу лаборатории (системному администратору, оператору).

МЕТОДИКА И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Методику выполнения работы рассмотрим на следующем примере.

Задан непрерывный сигнал s t , представляющий собой прямоугольный импульс высотой A = 1 В и длительностью τ = 1 мс = 10–3 с. Аналитическое описание сигнала представлено формулой

Требуется определить:

-верхнюю граничную частоту спектра fВ, Гц, и базу сигнала s t , исполь-

зуя энергетический подход;

-период tд, с, и частоту fД, Гц, дискретизации непрерывного сигнала

s t , удовлетворяющие теореме В. А. Котельникова;

-n – количество отсчетов дискретного сигнала (k = 0, 1, 2, … , n – 1);

-дискретный сигнал s k tд , полученный в результате дискретизации

непрерывного сигнала s t ;

-функции k t , составляющие базис Котельникова при восстановле-

нии исходного непрерывного сигнала s t по набору его дискретных отсчетов

s k tд (построить графики для нескольких первых базисных функций, напри-

мер, для k = 0, 1, 2, ...);

- несколько первых слагаемых, стоящих под знаком суммы в правой части формулы (2.3) и представляющих собой произведение k-го дискретного отсчета

10