1 вопрос: Виды уравнения прямой.

1. Ax +By+C=0 –Уравнение общего вида

2. У=kх+B –Уравнение с угловым коэффициентом

3. У-у₁=K(x-x₁) –Уравнение пучка прямых.

4. -Уравнение прямой проходящей через две заданные точки.

5. –Уравнение прямой в отрезках

2 вопрос: Деление отрезка в данном отношении. Определение площади треугольника по координатам его вершин.

2.1 ; ;;Если , тоX= x₁+x₂/2; У = у₁+у₂/2:

2.2 . -площадь треугольника по координатам вершины

3 вопрос: Угол между прямыми. Условие параллельности и перпендикулярности прямой.

3.1. Если уравнения прямой заданы в общем виде:A₁x+B₁y+C₁= 0,  A₂x+B₂y+C₂= 0 - угол между ними определяется по формуле:.

3.2. Условие параллельности:K₁=K₂; Условие перпендикулярности:

4 вопрос: Расстояние от точки до прямой

4.1.

5 вопрос: Уравнение окружности и эллипса.

1. (x – a)²+ (y – b)²= R²-уравнение окружности.

2. -Уравнение эллипса.

6 вопрос: Уравнение параболы и гиперболы.

6.1. - Уравнение параболы.

6.2. - Уравнение гиперболы.

7 вопрос: Общий вид уравнения линии второго порядка и его анализ.

Ax²+Bxy+Cy²+Dx+Ey+F=0 –общий вид уравнения линии второго порядка.

8 вопрос: Числовые последовательности. Предел последовательности. Свойства сходящихся последовательностей.

8.1. Числовой последовательностьюназывается числовая функция, заданная на множестве натуральных чисел или на множествепервых натуральных чисел.

8.2. Число А называется пределом числовой последовательности , если для любого, даже сколь угодно малого положительного числа, найдётся такой номерN, что для всех членов последовательности с номерамиn>Nверно неравенство.

8.3.1. Сходящаяся последовательность имеет только один предел;

2. Сходящаяся последовательность ограничена;

3. Если , то;

4.При любых постоянных и;

5.   ;

6. Если ,и, то;

7.Если , то;

8. Если и, то;

9. Если , то.

9 вопрос: Числовые множества . Грани числовых множеств. Абсолютная величина числа. Определение понятия непрерывной переменной.

9.1. Подмножествомпонимается совокупность (собрание, набор) некоторых объектов. Объекты, которые образуют множество, называются элементами, или точками этого множества.

9.2 Множество действительных чисел А называется ограниченным сверху, если существует такое действительное число М такое, что каждый элемент х множества А удовлетворяет неравенству x≤ M

При этом число М называется верхней гранью множества А.

Наименьшая из всех верхних граней ограниченного сверху множества AR называется точной верхней гранью.

Множество, ограниченное сверху и снизу называется ограниченным.

9.3. Абсолютной величиной (или модулем) действительного числа x называется само число x.

9.4.Переменная являетсянепрерывной переменной, если она может принимать бесконечное число значений в пределах определенного интервала.

10 вопрос: Понятие функции. Способы задания функции. Характерные особенности функции. Неявно заданная функция. Обратная функция.

10.1. Если каждому элементу х множества Х (х Х) ставится в соответствие вполне определённый элемент у множества У(уУ), то говорят, что на множестве Х заданнафункция у=f(x).

10.2. Способы задания функции:

А) Аналитический способ.

Б) Табличный

В) Графически

Г) Словесный способ

10.3. Характерные особенности функции:

1) Чётность и нечётность

2) Монотонность.

3) Ограниченность

4) Периодичность

10.4. Функция у аргумента х называется неявной, если она заданная уравнениемF= (x,y) = 0, не разрешённым относительно зависимой переменной. Пример: неявно задаёт две функции:

10.5.Функция х=, определённая на множестве У с областью значений Х называетсяобратной.

Например для функции обратной будет функция.

Вопрос 11: Предел функции в точке и в бесконечности. Левый и правый предел функции.

11.1.Число А называетсяпределом функции у=f(x),при х стремящемся кбесконечности, если для любого, даже сколь малого положительного числа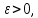найдётся такое положительное числоS>0, что для всех Х таких, чтоверно неравенство:

Число А называется пределом функции у=f(x),при х стремящемся кX₀, если для любого, даже сколь малого положительного числанайдётся такое положительное число>0, что для всех Х неравныхи удовлетворяющих условию: выполняется неравенство:

11.2. Предел, к которому стремится функция, когда х стремится к а, принимая только значения, меньшие (большие) а, называетсялевым (правым) пределом функциив точке а.

Вопрос 12: Основные теоремы о пределах функции.

1.Функция не может иметь более одного предела.

2.Предел алгебраической суммы конечного числа функции равен такой же сумме пределов этих функций т.е.

3.Предел произведения конечного числа функций равен произведению пределов этих функций. т.е.

.

4. Предел частного двух функций равен частному пределов этих функций. т.е.

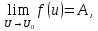
5.Если , то предел сложной функции

6.Если в некоторой окрестности точки X_0, f(x) <то

Вопрос 13: Замечательные пределы.

- Первый замечательный предел.

- Второй замечательный предел.

-Логарифмический предел.

- Степенной предел.

Вопрос 14: Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых функций.

14.1. Функцияy=f(x)называетсябесконечно малойприx→aили приx→∞, еслиили, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Функция f(x) называетсябесконечно большой величиной прих →х₀,если для любого, даже сколь угодно большего положительного числанайдётся такое положительное число δ>0, что для всех Х не равныхX₀и удовлетворяющих условию: будет верно неравенство:

14.2. Отношение бесконечно малых величин образует так называемуюнеопределённость.

Вопрос 15: Сравнение бесконечно больших функций. Связь между бесконечно малыми и бесконечно большими функциями.

15.1. 1), т.е. предел отношения функций существует и равен бесконечности. В этом случае говорят, что p(x)бесконечно большая функцияболее высокого порядка.

2) , т.е. предел отношения функций существует и равен С - некоторой константе. В этом случае говорят, что p(x) и q(x)бесконечно большие функцииодного порядка.

3) , т.е. предел отношения функций существует и равен нулю. В этом случае говорят, что q(x) бесконечно большая функция более высокого порядка.

4) Если данный предел: не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.

15.2.1) Еслиf(x) — бесконечно большая функция приx→x0, то— бесконечно малая функция приx→x0.

2) Если α(x) — бесконечно малая функция приx→x0   и   "xО (x0)α(x) ≠ 0,   то- бесконечно большая функция приx→x0.

Вопрос 16: Непрерывность функции в точке. Непрерывность сложной функции. Классификация точек разрыва.

16.1. Функция f(x), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т.е.

16.2. Если функция u(x) непрерывна в точке х0, а функция f(u) непрерывна в соответствующей точке u0 = f(x0), то сложная функция f(u(x)) непрерывна в точке х0.

16.3. При нарушении условия f(x0 − 0) = f(x0 + 0) = f(x0) точка x0 называется точкой разрыва функции f(x).

1) Если в точке x₀ существуют односторонние пределы f(x₀ − 0), f (x₀ + 0) и f(x₀-0)=f(x₀+0) ≠f(x₀) то точка х₀ называется точкой устранимого разрыва функции f(x)

2) Если в точке x₀ существуют односторонние пределыf(x₀− 0),f(x₀+ 0) иf(x₀− 0) ≠f(x₀+ 0), то точкаx₀называетсяточкой разрыва с конечным скачкомфункцииf(x)

3) Если в точке x₀хотя бы один из односторонних пределовf(x₀− 0),f(x₀+ 0) равенбесконечности или не существует, тоx₀называетсяточкой разрыва 2–го рода.