
- •1 Понятие языка программирования (неформально)
- •2 Эволюция языков программирования
- •3 Классификация языков программирования
- •4 Среда программирования
- •4.1 Понятие среды программирования
- •4.2 Техника разработки программ
- •4.3 Классификация ошибок в программе
- •4.4 Отладка
- •5. Основные виды языков программирования
- •6 Лямбда-исчисление как формализация функциональных языков
- •7 Лямбда-исчисление как формальная система
- •7.1 Свободные и связанные переменные
- •7.2 Подстановки
- •7.3 Конверсия
- •7.4 Равенство лямбда-термов
- •7.5 Экстенсиональность
- •7.6 Редукция лямбда-термов
- •7.7 Редукционные стратегии
- •8 Комбинаторы
- •9 Лямбда-исчисление как язык программирования
- •9.1 Представление данных в лямбда-исчислении
- •9.1.1 Булевские значения и условия
- •9.1.2 Пары и кортежи
- •9.1.3 Натуральные числа
- •9.2 Рекурсивные функции
- •9.3 Именованные выражения
- •10 Типы
- •10.1 Типизированное лямбда-исчисление
- •10.1.1 Базовые типы
- •10.1.2 Типизации по Черчу и Карри
- •10.1.3 Формальные правила типизации
- •10.2 Полиморфизм
- •10.2.1 let-полиморфизм
- •10.2.2 Наиболее общие типы
- •10.3 Сильная нормализация
- •11 Отложенные вычисления
- •12 Классы типов
- •13 Монады
Применение функции f к аргументу х мы будем обозначать как f х. Будем считать, что применение функции к аргументу ассоциативно влево, т.е. f х у означает (f(x))(y). В качестве сокращения для выражений вида λx. λy.Е будем использовать запись λху.Е (аналогично для большего числа аргументов). Будем считать, что «область действия» лямбда-выражения простирается вправо насколько возможно, т.е., например, λх.х у означает λх.(ху), а не (λх.х) у.
Существует операция каррирования, позволяющая записывать функции многих переменных в обычной лямбда-нотации. Она заключается в том, чтобы вы-
ражения вида λх у.х + у рассматривать как функцию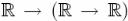 , т.е. еслиего применить к одному аргументу, результатом будет функция, которая принимает другой аргумент. Таким образом:
, т.е. еслиего применить к одному аргументу, результатом будет функция, которая принимает другой аргумент. Таким образом:
(λх у.х + у) 1 2 = (λу.1 + у) 2 = 1 + 2.
Переменные в лямбда-выражениях могут быть свободными и связанными. В выражении вида х2 + х переменная х является свободной; его значение зависит от значения переменной x и в общем случае ее нельзя переименовать. В подвыражении переменная может быть свободной, в то время как во всем выражении она может быть связана какой-либо операцией связывания переменной, такой как операция суммирования. Та часть выражения, которая находится «внутри» операции связывания, называется областью видимости переменной.
В лямбда исчислении выражения λх.Е[х] и λу.Е[у] считаются эквивалентными (это называется α-эквивалентностью, и процесс преобразования между такими парами называют α-преобразованием). При этом, необходимо наложить условие, что у не является свободной переменной в Е[х].
7 Лямбда-исчисление как формальная система
Лямбда-исчисление основано на формальной нотации лямбда-терма, составляемого из переменных и некоторого фиксированного набора констант с использованием операции применения функции и лямбда-абстрагирования. Это означает, что все лямбда-выражения можно разделить на четыре категории:
1. Переменные: обозначаются произвольными строками, составленными из букв и цифр.
15
2.Константы: также обозначаются строками; отличие от переменных будем определять из контекста.
3.Комбинации:, т.е. применения функции S к аргументу Т; и S и Т
могут быть произвольными лямбда-термами. Комбинация записывается как
ST.
4. Абстракции произвольного лямбда-терма S по переменной х, обо значаемые как λx.S.
Лямбда-терм определяется рекурсивно и его грамматику можно представить в виде следующей формы Бэкуса-Наура:
Ехр = Var | Const | Exp Exp | λ Var . Ехр
В соответствие с этой грамматикой лямбда-термы представляются в виде синтаксических деревьев, а не в виде последовательности символов. Отсюда следует, что соглашения об ассоциативности операции применения функции, эквивалентность выражений вида λxy.S и λx. λy.S, неоднозначность в именах констант и переменных проистекают только из необходимости представления лямбдатермов в удобном человеку виде, и не являются частью формальной системы.
7.1 Свободные и связанные переменные
Формализуем интуитивное представление о свободных и связанных переменных. Множество свободных переменных FV(S) лямбда-терма S можно определить рекурсивно следующим образом:
FV(x) = |
{х} |
FV(c) = |
Ø |
FV(ST) = |
FV(S) U FV(T) |
FV(λx.S) = |
FV(S) \ {x} |
Аналогично множество связанных переменных BV(S) определяется следующими формулами:
BV(x) = Ø
BV(c) = Ø
16

BV(ST) = BV(S) U BV(T)
BV(λx.S) = BV(S) U {x}
Здесь предполагается, что с — некоторая константа.
Пример. Для терма S = (λх у.х) (λx.z х) можно показать, что FV(S) = {z} и BV(S) = {x,y}.
7.2 Подстановки
Интуитивно ясно, что применение терма λx.S как функции к аргументу Т дает в результате терм S, в котором все свободные вхождения переменной х заменены на Т.
Будем обозначать операцию подстановки терма S вместо переменной х в другом терме Т как Т[х := S]. Правила подстановки можно определить рекурсивно. При этом необходимо наложить дополнительные ограничения, позволяющие избегать конфликта в именах переменных.
7.3 Конверсия
Лямбда-исчислене основано на трех операциях конверсии, которые позволяют переходить от одного терма к другому, эквивалентному ему. Эти конверсии обозначают греческими буквами а, (β и η). Они определяются следующим образом:
β-конверсия соответствует вычислению значения функции от аргумента, α- конверсия является вспомогательным механизмом для того, чтобы изменять имена связанных переменных, η-конверсия используется в основном при рас-
17

смотрении лямбда-исчисления с точки зрения логики.
7.4 Равенство лямбда-термов
Используя введенные правила конверсии, можно формально определить понятие равенства лямбда-термов. Два терма равны, если от одного из них можно перейти к другому с помощью конечной последовательности конверсии. Определим понятие равенства следующими выражениями, в которых горизонтальные линии следует понимать как «если утверждение над чертой выполняется, то выполняется и утверждение под ней»:
Следует отличать понятие равенства, определяемое этими формулами, от понятия синтаксической эквивалентности, которую будем обозначать специальным символом ≡. Например, λх.х ≠ λу.у, но λх.х = λу.у. Можно рассматривать синтаксическую эквивалентность термов с точностью до α-конверсий. Такую эквивалентность обозначают символом ≡а. Это отношение определяется так же, как равенство лямбда-термов, за тем исключением, что из всех конверсий допустимы только α -конверсии. Таким образом, λх.х ≡а λу.у.
7.5 Экстенсиональность
η-конверсия в лямбда-исчислении выражает собой принцип экстенсиональности. В общефилософском смысле два свойства называются экстенсионально эк-
18
