Mat_Analiz_Prokhorov

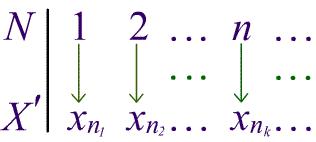
Установление такого отображения означает перечисление элементов счетного множества, записанного в форме последовательности. Эту мысль выразим предложением: множество X счетно тогда и только тогда, когда его можно представить в виде последовательности с попарно различными элементами.

Определим понятие подпоследовательности как подмножества последовательности, оставшегося после отбрасывания некоторых ее элементов.

Пусть дана последовательность

Перечислим номера тех ее элементов, которые остались после отбрасывания части членов последовательности. Пусть n1 - наименьший номер из оставшихся неотброшенными элементов, n2 - второй по порядку номер из оставшихся неотброшенными элементов и так далее. Пусть nk - это k-й по порядку номер из оставшихся неотброшенными элементов последовательности. Продолжим процедуру перечисления оставшихся неотброшенными элементов до бесконечности. Тогда последовательность

xn1, xn2, ..., xnk, ...

состоит из всех элементов, оставшихся после процесса отбрасывания и расположенных в порядке возрастания их номеров. Она называется подпоследовательностью исходной последовательности (1).

Рис. 2. Подпоследовательность исходной последовательности

21

2. Бесконечные подмножества счетного множества

Используем понятие подпоследовательности для доказательства следующей теоремы.

Теорема 1. Всякое бесконечное подмножество счетного множества является счетным множеством.

Доказательство. Пусть X - счетное множество. Его можно представить в виде последовательности попарно различных элементов

X = {x1, x2, ..., xn, ...}.

Предположим, что X - бесконечное подмножество множества X. Следовательно, X можно представить в виде подпоследовательности

X = {xn1, xn2, ..., xnk, ...}.

Поскольку подпоследовательность X в свою очередь является последовательностью попарно различных элементов, то X - счетное множество, что доказывает теорему 1.

Теорема 1 показывает, что счетные множества - наиболее "бедные" из бесконечных множеств. Невозможно придумать бесконечное множество, содержащееся в счетном множестве X, но не равномощное X.

3. Счетное объединение счетных множеств

Теорема 1 рассматривает бесконечные подмножества счетного множества и утверждает, что они остаются счетными. Попытаемся теперь объединить счетные множества и покажем, что счетное объединение не приведет к появлению более мощного множества.

Теорема 2. Объединение счетного множества счетных множеств является счетным множеством.

Доказательство. Пусть каждое из множеств X1, X2, ..., Xn, ... является счетным. Образуем множество

22

X = X1 X2 ... Xn ... = n = 1 Xn

и докажем, что X является счетным.

Каждое из счетных множеств представимо в виде последовательности попарно различных элементов. Поскольку каждое из объединяемых множеств имеет свой индекс, будем индексировать элементы последовательности двумя номерами: первый индекс отмечает номер объединяемого множества, второй индекс отмечает порядковый номер элемента последовательности

X1 = {x11, x12, ..., x1n, ...},

X2 = {x21, x22, ..., x2n, ...},

...........................................,

Xn = {xn1, xn2, ..., xnn, ...},

........................................... .

Множество X состоит из элементов, входящих в бесконечную матрицу с бесконечным числом строк и столбцов

23

(2)

Смысл доказательства заключается в изобретении способа перечисления элементов матрицы (2) в виде последовательности. Предложим один из таких способов. Начнем перечисление с элемента x11, находящегося в первой строки и первом столбце. Затем перечислим элементы, сумма индексов которых равна 3, то есть x12 и x21. Следом за этим перечислим элементы, сумма индексов которых равна 4, то есть x13, x22 и x31. И так далее. На очередном k-м шаге перечислим элементы, сумма индексов которых равна k + 1, то есть x1k, x2(k 1), ..., x(k 1)2, xk1. Будем продолжать процесс перечисления бесконечно. В итоге получится последовательность

x11, x12, x21, x13, x22, x31, ..., x1k, x2(k 1), ..., x(k 1)2, xk1, ...

которая содержит счетное множество элементов.

Рис. 3. Подпоследовательность Каждый элемент бесконечной таблицы (2) на некотором этапе действий появится в строке (3). Следовательно, строка (3) содержит

все элементы таблицы (2). Для того, чтобы выписать множество X, следует из последовательности (3) исключить повторяющиеся элементы, то есть отбросить элементы, появляюшиеся в (3) второй раз, третий и так далее. Оставшееся множество бесконечно как

24

объединение бесконечных множеств и поэтому по теореме1 оно является счетным как подмножество счетного множества (3), что доказывает теорему (2).

Применим теорему 2 для доказательства счетности множества рациональных чисел. Будем обозначать множество всех целых чисел через , а множество всех рациональных чисел - через .

Напомним, что рациональным числом называется отношение двух целых чисел. Значит, множество всех рациональных чисел

состоит из несократимых дробей m/n, где m и n - целые числа. Очевидно, n 0. Поскольку знак дроби зависит от комбинации знаков числителя и знаменателя, можно всегда считать, например, что n > 0, тогда как числитель m принимает значения положительные, отрицательные и нуль. Таким образом,

Теорема 3. Множество всех рациональных чисел счетно.

Доказательство. Прежде всего заметим, что множество всех целых чисел счетно как объединение счетного множества , равномощного ему множества отрицательных целых чисел и множества {0}, состоящего только из нуля.

Зафиксируем n и обозначим

Множество n равномощно множеству и поэтому оно счетно. Теперь по теореме 2 следует, что множество

= Qn

n 1

25

счетно как счетное объединение счетных множеств, что доказывает теорему 3.

4. Несчетность множества действительных чисел

Покажем, что в отличие от множества рациональных чисел множество действительных чисел не является счетным. Так как , то является более "мощным", чем .

Теорема 4. Множество несчетно.

Доказательство. Покажем, что множество 0 = [0, 1) несчетно. Всякое число a 0 изображается бесконечной десятичной дробью с целой частью a0, равной нулю. Проведем доказательство от противного. Предположим, что множество 0 счетно. Тогда

его можно перечислить в виде элементов последовательности a1, a2, ..., an, .... Каждое число an представимо бесконечной десятичной дробью без 9 в периоде. Запишем такие представления, снабдив цифры десятичного разложения двумя индексами: первый отмечает номер числа в последовательности, второй индекс отмечает порядковый номер цифры в десятичной дроби

Создадим новую бесконечную десятичную дробь без 9 в периоде, которой нет в перечне (4). Для этого выберем какую-либо цифру, отличную от 11 и от 9, и обозначим ее через 1. Далее выберем какую-либо цифру, отличную от 22 и от 9, и обозначим ее

через 2. И так далее. На n-м шаге выберем какую-либо цифру, отличную от nn и от 9, и обозначим ее через n. Продолжим процесс неограниченно.

В итоге получится бесконечная десятичная дробь

26

b = 0. 1 2... n...

без 9 в периоде. Число b не равно a1, так как первая цифра 1 десятичной дроби b не равна первой цифре 11 десятичной дроби a1 в первой строчке (4). Аналогично число b не равно a2, так как вторая цифра 2 десятичной дроби b не равна второй цифре 22 десятичной дроби a2 во второй строчке (4). И так далее. На n-м шаге заключаем, что число b не равно an, так как n-я цифра n десятичной дроби b не равна n-й цифре nn десятичной дроби an в n-й строчке (4). Продолжим неограниченно сравнение b с

числами в последовательности (4) и убедимся, что b не равно ни одному из чисел в (4). Таким образом, действительное число b 0 не перечислено в последователности (4), что противоречит допущению о счетности множества 0.

Полученное противоречие доказывает, что множество 0 несчетно. Аналогично все множества m = [m, m + 1), m , несчетны. Следовательно, и множество = m m несчетно, иначе бы его бесконечные подмножества m оказались бы счетными. Теорема 4 доказана.

Определение 3. Говорят, что множество имеет мощность continuum.

27

Лекция 3

1. Лемма об элементарном переходе к пределу в неравенствах 2. Границы и грани множества 3. Теорема существования верхней грани

4. Соотношение между гранями множества

1. Лемма об элементарном переходе к пределу в неравенствах

Мы построим вскоре строгую теорию последовательностей, в которой, в частности, сформулируем и докажем теорему о переходе к пределу в неравенствах. Однако предварительно мы должны вывести свойство полноты множества действительных чисел, а при этом нам необходимо воспользоваться элементарным правилом предельного перехода в неравенстве. Приведем это правило в следующей лемме.

Лемма 1. Пусть действительное число a для всех натуральных n удовлетворяет неравенству

(1) a 101 n .

Тогда a 0.

Пусть функции f и g дифферецируемы в точке x0. Тогда функции f + g, f g, fg и f/g дифференцируемы в точке x0 и справедливы формулы

Прокомментируем утверждение леммы 1. Интуитивно угадываем, что 1/10nстремится к 0 при n . Будь в нашем распоряжении теорема о переходе к пределу в неравенствах, мы применили бы ее к неравенству (1) и получили требуемое утверждение. Однако такая общая теорема не создана, как и весь аппарат теории пределов, поэтому приходится доказывать лемму 1 доступными на этом этапе средствами.

Доказательство леммы 1. Число a представимо бесконечной десятичной дробью

28

(2) a = a0 + 0. 1 2... n... .

Целое число a0 не может быть положительным, так как в противном случае справедливо неравенство a a0 1, противоречащее условию леммы для n = 1.

Если принять, что a0 < 0, то утверждение леммы 1 становится очевидным.

Предположим, что a0 = 0. Теперь цифра 1 не может быть положительной, так как в противном случае справедливо неравенство a 0. 1 0.1, противоречащее условию леммы 1 при n = 2. Следовательно, 1 = 0.

Если a0 = 0 и 1 = 0, то цифра 2 не может быть положительной, так как в противном случае справедливо неравенство a 0.0 2 0.01, противоречащее условию леммы 1 при n = 3. Следовательно, 2 = 0.

Предположим, что существует наименьшее натуральное число k такое, что цифра k положительна. Тогда справедливо неравенство

a 0.00...0 k 0.00...01,

противоречащее условию леммы 1 при n = k + 1. Полученное противоречие опровергает предположение, что k > 0. Таким образом, если в представлении (2) a0 = 0, то все цифры k, k , равны нулю, а это означает, что a = 0. Лемма 1 доказана.

2. Границы и грани множества

Важными примерами множеств на числовой оси служат отрезки [a, b], [a, b] = {x : a x b},

интервалы (a, b),

(a, b) = {x : a < x < b},

29

а также промежуточные множества [a, b) и (a, b], которые можно назвать полуотрезками или полуинтервалами, [a, b) = {x : a x < b},

(a, b] = {x : a < x b}.

Во всех четырех примерах точки a и b являются граничными. Приведем более точные определения.

Определение 1. Число M называется верхней границей множества X , если для всех x X выполняется неравенство x M.

Определение 1 верхней границы - первое в ряду многочисленных вводимых понятий математического анализа. В целях придания им унифицированной логической структуры будем в дальнейшем использовать два наиболее употребительных квантора, дающих

количественную характеристику области истинности предиката: квантор всеобщности x, означающий "для всех x", и квантор существования x, означающий "существует x" или "для некоторого x".

Таким образом, согласно определению 1, M - верхняя граница множества X, если

x X x M.

Определение 2. Число m называется нижней границей множества X , если

x X x m.

Определение 3. Множество X называется ограниченным сверху, если X имеет верхнюю границу, то есть если

30