mat.analiz_1

до одиниці, а процес вимірювання ОМ потрібно продовжити. Для цього відрізок ОЕ поділимо на 10 рівних частин, і знову можливі два випадки:

1)101 відрізка ОЕ відкладається у відрізку М1М ціле число α1 разів без

остачі. В цьому випадку процес вимірювання відрізка ОМ вважають завершеним, а точці М ставиться у відповідність раціональне число α0 ,α1, яке можна подати у вигляді нескінченного періодичного десяткового дробу: α0 ,α1000... =α0 ,α1(0).

2)101 відрізка ОЕ відкладається у відрізку М1М ціле число α1 разів з остачею М2 М, меншою від 101 ОЕ. Тут кажуть, що раціональне число

α0 ,α1 є результатом вимірювання відрізка ОМ з недостачею з точністю до 101 , а процес вимірювання ОМ можна продовжити.

Продовжуючи аналогічно міркування, прийдемо до висновку:

Висновок:

1)описаний вище процес вимірювання відрізка ОМ завершиться

на п му кроці, і точці М поставимо у відповідність раціональне

число α0 ,α1α2...αп , яке можна подати у вигляді нескінченного десяткового дробу α0 ,α1α2...αп000... =α0 ,α1α2...αп(0);

2)описаний вище процес вимірювання відрізка ОМ продовжиться необмежено, і ми отримаємо нескінченну послідовність раціональних чисел:

які є результатом вимірювання відрізка ОМ з недостачею з

Кожне з чисел послідовності (3.9) можна отримати обриванням

40

на відповідному десятковому знакові нескінченного десяткового дробу а =α0 ,α1α2...αп... (3.10)

Отже, кожній точці М числової осі ставиться у відповідність цілком конкретний нескінченний десятковий дріб (3.10)

Означення 3.11. Число а називають координатою точки М і позначають М(а), а числову пряму називають координатною прямою (віссю).

У таблиці наведено деякі підмножини множини дійсних чисел, які називають числовими проміжками:

41

ІІ спосіб. Використаємо геометричний зміст модуля. Нам потрібно знайти такі точки A(x) числової прямої, відстань від яких до точки

Приклад 4. Розв’язати нерівність x + 2 > 4 .

Розв’язання.

І спосіб. Використаємо означення модуля числа.

Остаточно маємо, що x (−∞;−6) (2;+∞)

ІІ спосіб. Використаємо геометричний зміст модуля. Нам потрібно знайти такі точки A(x) числової прямої, відстань від яких до точки

f (x) > a, a > 0 f (x)> a,

f (x)< −a

43

або

Означення 4.4. Множину А називають необмеженою зверху, якщо для довільного числа a R існує число x A таке, що x > a .

Скорочений запис:

Запишіть означення необмеженої знизу ї необмеженої множин!

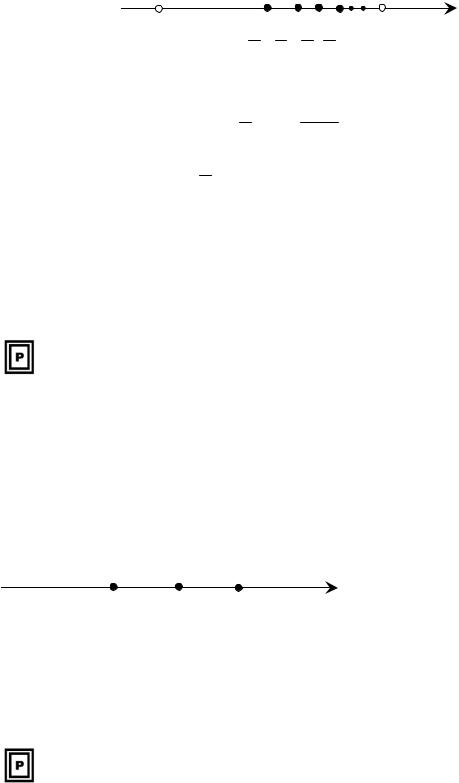
45

Очевидно, що n N: 12 ≤1 − n 1+1 <1, тому вказана множина є обмеженою, а числа 12 і 1 є відповідно нижньою і верхньою межами.

Варто зауважити, що якщо обмежена зверху множина має верхню межу, то вона їх має безліч. Наприклад, числа 2,1; 2,999; 3, 5,

10, … є верхніми межами променя (−∞,2).

Означення 4.7. Найменшу з усіх верхніх меж непорожньої, обмеженої зверху множини А називають точною верхньою

межею цієї множини і позначають sup A.

В перекладі з латинської мови «supremum» означає «найбільший».

Умова 10 вказує на обмеженість зверху множини А, а умова 20 вказує на те, що меншого від а числа, яке обмежує зверху множину А, немає (рис.4.2).

Означення 4.8. Найбільшу з усіх нижніх меж непорожньої, обмеженої знизу множини А називають точною нижньою межею цієї множини і позначають inf A .

В перекладі з латинської мови «infimum» означає «найменший»

46

правильна, отже перша умова виконується.

X1 + X 2 +...+ X n := {x R x = x1 + x2 +... + xn , x1 X1, x2 X 2 ,...xn X n }

Різницею X −Y множин Х і Y називається множина:

X −Y :={z z = x − y, x X , y Y}.

Означення 4.10. Добутком λX числа λ на числову множину Х називається множина:

λX :={ y y =λx, x X }.

Добутком XY двох числових множин Х і Y називається множина всіх чисел z , які можна подати у вигляді:

XY :={z z = xy, x X , y Y }.

47

десятковий знак через α2 . Міркуючи аналогічно, ми визначимо десяткові знаки деякого числа a = α0 ,α1α2 ...αn ... (4.8)

Покажемо, що число а є точною верхньою межею множини А, тобто: 1) а є верхньою межею множини А і 2) а є найменшою з усіх верхніх меж.

Перше твердження доводимо методом від супротивного. Припустимо, що в множині А існує число x = x0 , x1x2 ... xn ... таке, що

x > a . Отже, згідно з означенням 3.4 порівняння дійсних чисел,

оскільки в числі а за αk вибиралася найбільша цифра з десяткових знаків xk тих чисел х, у яких ціла частина і перші k −1 знаків після коми відповідно дорівнюють α0 ; α1; ...; αk −1 . Отже, x ≤ a .

Щоб довести друге твердження, потрібно показати, що для довільного числа x' A і x'< a знайдеться число x" A таке, що x"> x'. Отже, нехай x' = x'0 , x'1 x'2... x'n .... З умови x '< a і означення 3.4 порівняння дійсних чисел знайдеться номер т такий, що x'0 =α0 ,

побудовою чисел, і x"> x', що й потрібно було довести.

Отже, a = α0 ,α1α2 ...αn ... є точною верхньою межею множини А.

Аналогічно дана теорема доводиться і для випадку, коли x A і x ≤ 0 .

Принцип Вейєрштрасса виражає неперервність множини дійсних чисел.

Означення 4.11. Послідовність відрізків

49