
mat.analiz_1
.pdf
План:
1.Числові послідовності, способи задання і операції над ними.
2.Границя числової послідовності. Необхідна умова збіжності.
3.Основні властивості збіжних числових послідовностей.
Мета лекції: дати означення числової послідовності і границі числової послідовності, виділити клас збіжних числових послідовностей і вивчити їх властивості. Показати, що границя числової послідовності характеризує поведінку її членів з достатньо
великими номерами.
 Числові послідовності, способи задання і операції над ними.
Числові послідовності, способи задання і операції над ними.
Означення 7.1. Сукупність чисел y1 , y2 , y3 , ...., yn , .... (7.1), які є значенням функції y = f (n) натурального аргументу і які записано в порядку зростання аргументу, називають числовою послідовністю. Числа y1 , y2 , y3 , ...., yn , .... називають членами послідовності відповідно першим, другим і т.д., yn називається n м або загальним членом послідовності.
Позначають y1 , y2 , y3 , ...., yn , .... , або {yn }, або (yn ), або yn = f (n), n =1, 2 ,.... .
Оскільки числова послідовність є окремим випадком функціональної залежності, то способи задання числової послідовності ті ж самі, що й функції, а саме: числова послідовність вважається заданою, якщо вказано закон або правило, за яким кожному натуральному числу n ставиться у відповідність дійсне число yn .
а) Задання послідовності за допомогою формули.
 Приклади:
Приклади:
90

1.yn = n2 ; 1; 4; 9; 16; ...; n2 ; ...;
2.yn = (−1)n ; −1; 1; −1; 1;... ,
3.(1 ); 1; 1; 1; 1; ... ,
4.yn = sin 1n ; sin1; sin 12 ; sin 13;...;sin 1n ;...
б) Задання послідовності рекурентним способом, за яким задається декілька перших членів і правило утворення n го члена за допомогою попередніх членів.
 Приклади:
Приклади:
5. y1 = 2 ; yn |
= 5 yn−1 , тобто 2;10; 50; 250; 750; ...; |
|
||||
6. |
[18,с.44] |
послідовність |
(xn ) |
задана |
рекурентно: |
|
y1 |
= y2 =1, |
yn+2 |
= 5 yn+1 −6 yn , n ≥1. |
Знайти |
формулу |
загального |
члена цієї послідовності.
Розв’язання. Знайдемо всі послідовності вигляду (qn ), q R , які задовольняють рівність:
|
|
|
|
|
|
|
|
|
an+2 = 5an+1 − 6an ; n ≥1. |
|
||||
Підставимо |
|
|
a |
|
= qn , a |
= qn+1 , a |
|
= qn+2 |
отримаємо |
|||||
|
|
|
|
|
|
|
n |
n+1 |
|
n+2 |
|
|
||
q |
n+2 |
−5q |
n+1 |
+ 6q |
n |
= 0 q |
2 |
−5q + 6 = 0 |
q = 2, |
|
||||
|
|
|
|
q1 |
= 3. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Отже, |
послідовності (2n ) і |
(3n ) |
задовольняють рекурентному |
|||||||||
співвідношенню. Знайдемо значення сталих c1 і c2 , при яких
послідовність |
|
(a |
n |
), |
де |
a |
n |
= c 2n + c |
2 |
3n , |
|
також задовольняє |
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
рекурентному співвідношенню і a1 = a2 =1: |
|
|
|
|
|||||||||||||||
|
1 |
c |
|
|
1 |
|
=1, |
|
|
2c |
+3c |
= |
1, |
|
c |
=1, |
|||
2 |
|
|
+3 c |
|
|
|
|
1 |
= −1. |
||||||||||
|
2 |
2 |
1 |
|
|
2 |
2 |
=1, |
{2c1 |
+3c2 |
= |
0, |
c |
||||||
|
|
c |
|
|
+3 |
c |
|
|
1 |
2 |
|
|
|
|
|
2 |
3 |
||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, формула загального члена набирає вигляду:
yn = 2n −3n−1, n ≥1.
91
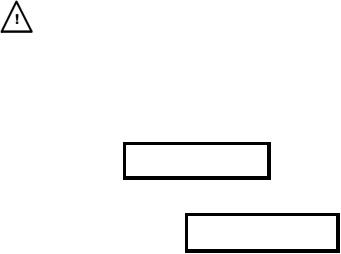
7. Послідовність |
|
|
(yn ) |
|
|
задана |
|
рекурентно: |
y1 = 2; |
y2 |
= 3; |
|||||||||||||||
yn+2 = 6 yn+1 −9 yn |
|
при n ≥1. Знайти формулу загального члена. |
|
|
||||||||||||||||||||||
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Знайдемо |
|
|
всі |
|
|
послідовності |
вигляду |
(qn ), q R , |
які |
|||||||||||||||||
задовольняють рівність: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
an+2 = 6an+1 −9an ; n N . |
|
|
|
|
|
|
|||||||
Підставимо |
|
|
a |
|
= qn , |
|
|
a |
= qn+1 , |
a |
n+2 |
= qn+2 , |
|
отримаємо |
||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
n+1 |
|
|
|
|
|
|
|
|
|
|
|
|||
qn+2 = 6qn+1 −9qn q |
2 − 6q + 9 = 0 q = q |
2 |
= 3. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Легко |
перевірити |
|
безпосередньою |
|
|
підстановкою, |
що |
|||||||||||||||||||
послідовності |
(3n ) |
|
|
і |
|
(n3n ), а значить і |
|
(c13n + c2n3n ), c1,c2 R , |
||||||||||||||||||
задовольняють рекурентній формулі. Знайдемо сталі c1 і c2 : |
|
|
||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
c1 = |
1, |
|
|
|
a |
= 2, |
|
3 c |
|
|
+ |
3 |
|
1 c = 2, |
|
3c +3c |
|
= 2, |
|
|
|
|
|
||||||||
{a1 = 3, |
|
|
2 |
|
1 |
|
|
2 |
|
2 |
3, |
{6c1 |
+152c |
|
= |
3, c = −1. |
|
|
||||||||
|
2 |
|
3 |
|
c |
|
|
+3 |
|
2 c = |
|
1 |
|
2 |
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже, формула загального члена набирає вигляду |
|
|
|
|
|
|||||||||||||||||||||
yn = (1− n3)3n = (3 −n)3n−1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Зауваження. Якщо послідовність (yn ) задана рекурентною |
|||||||||||||||||||||||||
формулою: |
|
|
|
|
|
y1 = a; y2 = b; yn+2 + pyn+1 + qyn |
= 0, n N , |
то |
||||||||||||||||||
формула загального члена знаходиться за алгоритмом: |
|
|
||||||||||||||||||||||||
а) |
якщо рівняння |
λ2 + pλ + q = 0 має різні і дійсні корені λ |
і |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
λ2 , то |
|
|
|
|
|
|
|
|
|
|
|
, c1 і c2 – деякі сталі; |
|
|
|
|
|
|||||||||
б) |
якщо рівняння |
λ2 + pλ + q = 0 має рівні дійсні корені |
λ |
і |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
λ |
= λ, |
то |
|
|
yn = |
(c1 + c2n)λn , |
c |
і c |
|
|
– |
деякі |
сталі, |
які |
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
знаходяться з умовами y1 = a, |
y2 = b . |
|
|
|
|
|
|
|
|
|
||||||||||||||||
92
8. (Числа Фібоначчі) (yn ): y1 = y2 =1, yn+2 = yn+1 + yn , n N , тобто
1; 1; 2; 3; 5; 8; 13; 21; 34; ...
Виходячи з зауваження, знайдемо розв’язок квадратного рівняння:
λ |
= |
1− |
5 |
, |
|||
|
|
|
|||||
λ2 −λ −1 = 0 |
1 |
2 |
5 |
Загальний член yn набере вигляду: |
|||
λ |
= |
1+ |
. |
||||
|
|
||||||
|
2 |
2 |
|
|
|
||
|
|
|
|
|
|||
y |
|
= c |
|
|
1+ |
5 |
n |
+c |
|
1− |
5 |
n |
, де c і |
c |
– деякі сталі, які знайдемо з |
||||||||||||||||
n |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
1 |
2 |
|
2 |
|
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
умови: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 5 |
|
|
|
1− 5 |
|
|
|
c |
|
1 |
|
|
|||||
|
|
|
|
|
|
{yy1 ==1,1, |
c1 |
|
|
+ c2 |
|
|
|
=1, |
= |
, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
51 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
1+ 5 |
|
|
1− 5 |
|
|
c |
= − |
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ c2 |
|
|
|
=1, |
|
2 |
|
|
5 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
c1 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже,
Останню формулу називають формулою Біне.
Арифметичні операції над числовими послідовностями.
Нехай маємо дві числові послідовності:
|
|
|
|
|
|
x1 , x2 , x3 ,..., xn ,..., |
|
(7.2) |
|
|
|
|
|
|
|
y1 , y2 , y3 , ...., yn , .... . |
(7.1) |
||
Тоді суму, добуток і частку числової послідовності означають |
|||||||||
через рівності: |
|
|
|
|
|
|
|
||
(xn )+ (yn ):= (xn + yn ), |
|
|
|||||||
(xn ) (yn ):= (xn yn ), |
|
|
|||||||
|
(xn ) |
|
|
|
|
xn |
|
|
|
|
|
:= |
|
|
yn |
≠ 0, n N . |
|||
|
|
|
|||||||
|
(yn ) |
|
|
|
при умові, що |
||||
|
|
yn |
|
|
|||||
Означення 7.2. Якщо |
|
n1 , n2 , n3 , ...., nk , .... |
|
деяка нескінченна |
|||||
підмножина множини натуральних чисел N , то послідовність
93

yn |
, yn |
2 |
, yn , ...., yn |
k |
, .... |
називають |
підпослідовністю |
1 |
|
3 |
|
|
|
послідовності 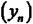 .
.
 Пр иклади:
Пр иклади:
9. (n): 1; 2; 3; 4; 5; 6; 7; 8;...
↓ |
↓ |
↓ |
↓ |
2; |
4; |
6; |
8;.... |
Отже, (2n) є підпослідовністю послідовності (n) .
10. |
|
1 |
1; |
1 |
; |
1 |
1 |
|
1 |
; |
1 |
; _ |
1 |
|
|
(n): |
2 |
3; |
4 ; |
|
5 |
6 |
7 ;... |
|
|||||||
|
|
↓ |
|
|
|
↓ |
|
|
↓ |
|
|
|
↓ |
|
. |
|
|
1; |
|
|
__ .1 |
; ____ . |
1 |
; |
|
|
1 |
;... |
|||
|
|
|
|
|
|
3 |
|
|
5 |
|
|
|
7 |
|
|
Отже, ( |
1 |
|
) |
є підпослідовністю послідовності (1). |
|||||||||||
|
|
||||||||||||||
|
|
2n −1 |
|
|
|
|
|
|
|
|
|
|
n |
||
Означення 7.3. Числова послідовність називається обмеженою зверху, якщо існує число М, що для будь якого n N виконується нерівність yn ≤ M .
|
|
df |
|
|
|
|
|
|
|
|
|
|
|
xn ≤ M ); |
|
((xn ) −обмежена зверху) ( M , n |
N : |
||||||||||||||
|
|
df |
|
|
|
|
|
|
|
|
|
|
|
xn ≥ K ); |
|
((xn ) −обмежена знизу) ( K, |
n N : |
||||||||||||||
|
df |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
((xn ) −обмежена ) ( H , n N : |
|
xn |
|
|
≤ H ). |
||||||||||
|
|
||||||||||||||
Приклад: |
|
|
|
|
5 |
|
|
|
|
|
|
||||
11. Довести, що послідовність (x ), |
x |
= |
|
, є обмеж еною. |
|||||||||||
6n + 2 |
|||||||||||||||
|
n |
|
n |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Доведення. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n ≥1, |
≥ 6 1 + 2 = 8, |
|
|||||||||||||
6n + 2 |
|
||||||||||||||
|
1 |
≤ |
1 |
, __ |
|
5 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||
6n + 2 |
|
|
|
|
|
|
|||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5 |
≤ |
5. |
|
|
|
|
|
|
|
|
|
|
||
6n + 2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
||
Отже, існує число M = 5 |
таке, щ о n N : |
0 ≤ x ≤ 5 |
, або |
|
x |
|
≤ 5 . |
|
|
|
|||||||
8 |
|
n |
8 |
|
|
n |
|
8 |
94
12. Довести, що послідовність (x ), |
x = |
1000n |
є обмеженою. |
|
|||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
n |
n |
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доведення. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Оскільки xn > 0 |
n N , то |
оцінимо |
відношення наступного |
||||||||||||||
члена до переднього: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
xn+1 =1000n+1 |
|
|
n! |
=1000 . |
|
|
|
||||
|
|
|
|
|
|
xn |
|
(n +1)! |
|
1000n |
|
n +1 |
|
|
|
||
|
xn+1 |
≥1 1000 ≥1 1 |
≤ n ≥ 999 , тобто x |
≤ x |
≤ x |
, |
|||||||||||
|
|
|
|||||||||||||||
|
xn |
n +1 |
|
|
|
|
|
|
|
1 |
n |
999 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
xn+1 |
≤1 1000 ≤1 n |
|
≥ 999 |
, тобто x |
≤ x . |
|
||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
xn |
|
n +1 |
|
|
|
|
|
n |
999 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отже, n N правильні нерівності: |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
0 < x < x |
=1000999 , |
|
|
|
||||||
|
|
|
|
|
|
|
|
n |
999 |
999! |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тому дана послідовність обмежена.
Границя числової послідовності. Необхідна умова збіжності.
Розглянемо числові послідовності (xn ),(yn ),(zn ),(un ) та позначимо кілька їх членів точками на числовій осі.
1. xn = 1n , n N :
|
x5 |
x4 |
x3 |
0 |
1 |
1 |
1 |
5 |
4 |
3 |
x2 |
x1 |
|
1 |
x |
|
1 |
||
2 |
||
|
2. yn = 2 + (−n1)n , n N :
x1
0 |
1 |
x |
|
x |
4 |
x2 |
|
3 |
|
|
|
|
|
5 |
|
9 |
5 |
y |
|
2 |
3 |
||||
3 |
|
4 |
2 |
|
|
3. z1 =1; z2 =1, 7; z3 =1, 73; z4 =1,732; z5 =1, 7320; z6 =1, 73205,...:
95
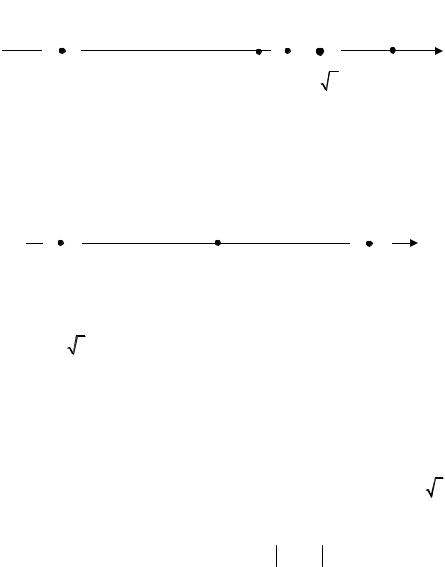
z1
1
4. un = (−1)n , n N :
u3
u1
1
z2 |
z3 |
z4 |
z
1,7 |
1,73 |
3 |
2 |
u4
u2
u
0 |
1 |
Для кожної з послідовностей (xn ), (yn ), (zn ) існує єдине число (відповідно 0, 2, 3 , до якого наближаються члени послідовності із зростанням номера n). Для послідовності такого числа немає: члени послідовності з парним індексом попадають у точку 1, а члени послідовності з непарним індексом – у точку –1.
Символічно процес наближення членів послідовності до числа а можна записати так: xn → 0, n → ∞; yn → 2, n → ∞; zn → 3, n → ∞.
Це означає, що із зростанням номера n , наприклад для відстань від точки yn до точки 2, тобто yn −2 , зменшується. Виникає запитання: чи може ця величина стати меншою за 0,01; 0,001; 0,0001 і взагалі меншою за будь яке наперед задане як завгодно мале додатне число ε ?
З'ясуємо, наприклад, коли (для яких номерів n) виконува тиметься нерівність:
або |
|
|
|
yn −2 |
|
< 0,01, |
|
(7.3) |
|||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
yn |
− 2 |
|
= |
|
(−1)n |
|
= |
1 |
< 0,01. |
|
(7.4) |
|||
|
|
|
|
|
|||||||||||
|
|
|
|
||||||||||||
|
|
|
n |
|
n |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||
Для виконання нерівності (7.3) треба, щоб 1 |
< 0,01, звідки |
n >100 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
Номерами n , які задовольняють останню нерівність, є 101, 102, ...,
96

тобто всі натуральні числа, починаючи з n = 101.
Нерівність yn −2 <0,001 виконується для n = 1001, 1002, ... .
Геометрично цей результат означає, що всі члени yn послідовності, коли n ≥101 , знаходяться від точки 2 на відстані, яка менша за 0,01, тобто попадають в окіл точки 2.
1,99 |
|
2,01 |
y101 |
2 |
y102 |
Рис.7.1
Аналогічно можна розв'язати поставлене запитання для даної послідовності, задавши будь яке інше додатне число, тобто в загальному випадку
y −2 |
|
<ε ; 1 |
<ε ; |
n > 1 ≥ 1 |
|
= n . |
|
|
|||||||
n |
|
n |
|
ε |
|
|
0 |
|
|
||||||
|
|
|
ε |
|
|
||
В цьому випадку кажуть, що число 2 є границею послідовності
(yn ) і записують lim yn = 2 .
n→∞
Якщо |
аналогічні міркування провести |
для |
послідовностей |
(xn ), (zn ), |
то можна переконатися, що числа 0 |
і 3 |
є відповідно їх |
границями.
У загальному випадку для числової послідовності (xn ) дамо означення границі.
Означення 7.4. Число а називають границею числової послідовності (xn ), якщо для будь–якого як завгодно малого
додатного числа ε > 0 існує такий номер n0 |
= n0 |
(ε ), що при всіх |
||||
n > n0 виконується нерівність |
|
xn − a |
|
< ε |
|
|
|
|
|
|
|||
і позначають |
|
|
||||
lim xn = a , або xn → a при n → ∞, або xn |
→ a . |
|||||
n→∞ |
|
n→∞ |
||||
Символічно це означення можна записати:
(7.5)
97
Означення 7.5. Послідовність, яка має скінченну границю, називається збіжною, у протилежному випадку – розбіжною.
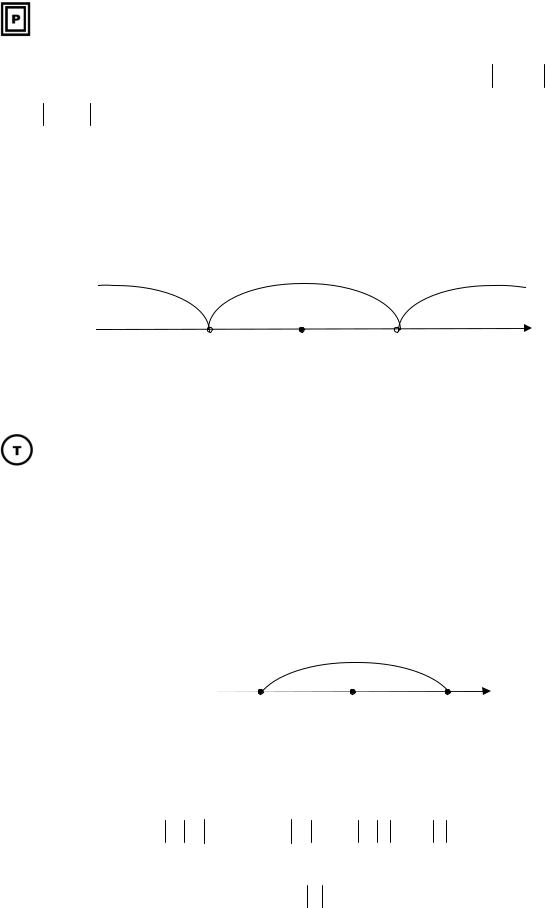
Здійснимо рівносильні перетворення нерівності xn − a < ε : xn −a <ε −ε < xn −a <ε a −ε < xn < a +ε xn (a −ε;a +ε).
Геометрично це означає: який би окіл точки а ми не взяли, всі члени xn послідовності, починаючи з деякого номера n > n0 , попадають в цей окіл (так що поза цим околом може залишитись тільки скінченне число членів послідовності) (рис. 7.2).
скінченне число безліч скінченне число
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
xn0 |
a −ε x |
+2 |
|
а |
|
xn +1 a +ε |
|
x1 |
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
n |
|
|
|
|
0 |
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.2
Теорема 7.1 (необхідна умова збіжності) Будь яка збіжна послідовність обмежена.
Доведення.
|
df |
(ε =1), n , n |
|
|
|
|
|
|
|
lim x |
= a ε > 0 |
> n |
: |
|
x − a |
|
<1; |
||
|
|
||||||||
n→∞ n |
|
0 |
0 |
|
|
n |
|
|
|
|
|
|
|
||||||
|
|
−1 < xn − a <1, |
|
+a ; |
|||||
|
|
|
|||||||
a −1 < xn < a +1.
|
|
|
а |
|
|
|
х |
а 1 xn +1 |
|
|
|
||||
|
xn +1 а+1 |
||||||
0 |
|
|
0 |
|
|
||
Рис.7.3
Оцінимо
xn = (xn − a)+ a ≤ xn −a + a <1+ a , n > n0 .
Отже, всі члени послідовності, починаючи з деякого номера, за модулем стають менші від числа a +1.
98

Визначимо |
число |
|
{ 1 |
2 |
|
|
n0 |
} |
= M , |
тоді |
||||||||||||
M = max |
|
x |
|
, |
|
x |
|
,..., |
x |
, |
|
a |
|
+1 |
||||||||
|
|
|
|
|
|
|||||||||||||||||
n N : |
|
xn |
|
≤ M . Отже, послідовність (xn ) |
обмежена. |
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||||
Обмеженість числової послідовності є необхідною умовою збіжності числової послідовності. Обернене твердження, взагалі кажучи, неправильне.
 Приклад:
Приклад:
13. Розглянемо числову послідовність {(−1)n}. Тут
(−1)n ≤1 n N , тобто послідовність обмежена, однак
границя її не існує.
 Основні властивості збіжних числових послідовностей.
Основні властивості збіжних числових послідовностей.
Теорема 7.2 (єдиність границі) Збіжна числова послідовність може мати тільки одну границю.
Доведення проведемо методом від супротивного. Припустимо,
що числова послідовність (xn ) |
має дві різні границі a і b, a ≠ b . За |
||||||||||||||||||||||||||||||||||||||||||||||||||||
означенням границі маємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
df |
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< ε |
, |
|
(7.6) |
|
|||||||
|
lim x |
|
|
|
= a ε > 0 |
|
, |
n , n > n : |
|
|
|
x |
− a |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
n→∞ n |
|
|
|
|
|
|
|
df |
|
|
(2) |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
n |
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε . |
|
(7.7) |
|
|||||
|
lim x |
|
|
|
= b ε > 0 |
|
|
, |
|
|
|
|
n , |
|
|
|
n > n : |
|
x −b |
|
< |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
n→∞ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
n |
|
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
Виберемо |
|
|
|
max{n1,n2}= n0 , |
тоді нерівності (7.6) і (7.7) |
|||||||||||||||||||||||||||||||||||||||||||
виконуватимуться одночасно. Оцінимо відстань між числами |
a і b: |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a −b |
|
= |
|
|
|
a − x |
+ x |
|
−b |
|
≤ |
|
x |
− a |
|
+ |
|
x |
−b |
|
< ε + ε = ε |
для всіх n > n |
, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
2 |
2 |
0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
або |
|
|
|
a −b |
|
<ε . Оскільки |
– довільне додатне число, то виберемо |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
ε = |
|
|
a − b |
|
|
, тоді |
|
a − b |
|
< |
|
|
a − b |
|
|
, або 1 < 1 . |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Отримали суперечність, яка виникла в припущенні існування двох різних границь. Значить, a =b.
99
