
Prak_Geom1
.pdf
Означення 1.11. Афiнними координатами точки M вiдносно репера (O;~e1;~e2) (â àôiííié
¡¡!
системi координат O~e1~e2) 9 називають координати x; y радiус-вектора OM вiдносно базису
(~e1;~e2).
Число x називають абсцисою, а y ординатою точки M i при цьому записують M(x; y). Ç
означення виплива¹, що кожнiй точцi M площини вiдповiда¹ пара чисел (x; y) множини R, à
в силу ¹диностi подання (1.18) рiзним точкам площини вiдповiдають рiзнi елементи множини R£R. Навпаки, для кожного елемента (x; y) ç R£R можна вказати вектор x~e1 + y~e2, à îòæå,
iсну¹ точка M, äëÿ ÿêî¨ ïàðà (x; y) ¹ ¨¨ координатами. Це означа¹, що мiж точками площини i
елементами множини R£R афiнна система координат O~e1~e2 встановлю¹ вза¹мно однозначну âiäïîâiäíiñòü.
Означення 1.12. Афiнну систему координат (O;~e1;~e2) називають декартовою системою координат, якщо j~e1j = j~e2j = 1 (вектори базису ¹ одиничнi вектори), а декартову систему координат називають прямокутною декартовою системою координат, якщо вектори ~e1 i ~e2 ортогональнi.10
Нехай в афiннiй системi координат O~e1~e2 точки A(x1; y1) i B(x2; y2) заданi координатами,
необхiдно знайти координати вектора |
¡¡! |
|
|
|||
AB . Справдi, за правилом трикутника ма¹ мiсце |
||||||
¡¡! |
¡¡! |
¡¡! |
¡¡! |
¡¡! |
¡¡! |
¡¡! ¡¡! |
ðiâíiñòü OA + AB = OB , çâiäêè |
AB = OB ¡ OA . Îñêiëüêè |
OA ; OB ¹ радiус-вектори |
||||
вiдповiдно точок A i B, то, очевидно, координати цих векторiв такi ж самi, як у вiдповiдних |
||||||
точок, тобто |
¡¡! |
¡¡! |
|
|
¡¡! |
|
OA (x1; y1) i OB (x2; y2). Îòæå, |
AB (x2 ¡ x1; y2 ¡ y1), тобто щоб знайти |
|||||
координати вектора |
¡¡! |
|
|
|
|
|
AB необхiдно вiд координат кiнця вектора вiдняти координати його |
||||||
початку. Якщо ж точки A i B заданi координатами в прямокутнiй декартовiй системi |
||||||
¡¡!
координат, то ми можемо знати вiдстань AB мiж цими точками, оскiльки AB = j AB j.
Таким чином, ми отриму¹мо наступну формулу:
p
AB = (x2 ¡ x1)2 + (y2 ¡ y1)2:
Дану формулу застосовують для знаходження рiвняння кола. Вiдомо, що коло !(C0; R) ç
центром в точцi C0(x0; y0) i ðàäióñîì, ðiâíèì R, ¹ геометричне мiсце точок рiвновiддалених
âiä öåíтра на вiдстань радióñà. Îòæå, ÿêùî M(x; y) довiльна точка кола, то C0M = R, |
||||||
òîìó p(x ¡ x0)2 + (y ¡ y0)2 = R, çâiäêè |
2 |
+ (y ¡ y0) |
2 |
2 |
: |
(1.19) |
(x ¡ x0) |
|
|
= R |
|||
Рiвняння (1.19) називають канонiчним рiвнянням кола.
Нехай M1, M2, M ¹ три точки однi¹¨ прямо¨, а ¸ деяке дiйсне число.
Означення 1.13. Будемо казати, що точка M дiлить направлений вiдрiзок M1M2 ó вiдношеннi ¸, якщо викону¹ться рiвнiсть
|
¡¡! |
¡¡! |
|
(1.20) |
|
|
|
M1M= ¸ MM2 : |
|
||
9 |
Часто ми замiсть (O;~e1;~e2) будемо використовувати запис O~e1~e2. |
|
|
||
10 |
Надалi базиснi вектори в прямокутнiй декартовiй системi координат ми позначатимемо через ~, ~ |
. Îòæå, |
|||
прямокутну декартову систему координат ми завжди будемо позначати через |
i j |
|
|||
~~. |
|
||||
|
|
|
|
Oi j |
|
21

Зауважимо, що з (1.20) виплива¹, що ¸ =6 ¡1. Справдi, якщо припустити, що ¸ = ¡1, òî
¡¡! |
|
¡¡! |
|
¡¡! |
¡¡! |
~, òîìó |
M1M= ¡ MM2, çâiäêè M1M + MM2= 0 |
||||||
¡¡! |
~ |
. Îòæå, |
M1 |
= M2, що суперечить тому, |
||
M1M2= 0 |
|
|||||
що данi точки рiзнi. Вiдмiтимо також, що |
||||||
|
|
|
|
¡¡! ¡¡! |
|
|
ïðè ¸ > 0 вектори M1M i MM2 |
спiвнаправленi, а при ¸ < 0 вони протилежно направленi. |
|||||
В першому випадку кажуть, що точка M äiëèòü âiäðiçîê M1M2 внутрiшнiм чином, а в другому зовнiшнiм. При внутрiшньому подiлi точка M знаходиться мiж кiнцями вiдрiзка,
а при зовнiшньому за його межами.
Розглянемо афiнну систему координат O~e1~e2 i нехай в цiй системi координат данi точки мають такi координати: M1(x1; y1), M2(x2; y2), M(x; y). Ìà¹ìî
тому з (1.20) отриму¹мо Отже,
¡¡! |
¡¡! |
|
¡¡! |
¡¡! |
¡¡! ¡¡! |
|
||
M1M = OM ¡ OM1; MM2 = OM2 ¡ OM ; |
|
|||||||
¡¡! |
¡¡! |
|
¡¡! |
¡¡! |
¡¡! ¡¡! |
¡¡! |
||
OM ¡ OM1 |
= ¸(OM2 ¡ OM ), çâiäêè (1 + ¸) OM =OM1 |
+¸ OM2. |
||||||
|
¡¡! |
|
1 |
¡¡! |
|
¡¡! |
(1.21) |
|
|
OM = |
|
|
(OM1 |
+¸ OM2): |
|||
|
1 + ¸ |
|||||||
З формули (1.21) отриму¹мо афiннi координати точки подiлу M:
|
|
x = |
x1 + ¸x2 |
; |
y = |
y1 + ¸y2 |
; |
|
|
|
|
|
|||||
|
|
|
1 + ¸ |
|
1 + ¸ |
|
||
оскiльки радiус-вектори |
¡¡! ¡¡! |
¡¡! |
|
|
|
|
||
OM , OM1 |
, OM2 мають координати вiдповiдних точок, а саме: |
|||||||
¡¡! |
¡¡! |
|
|
|
|
|
|
|
(x; y), OM1 (x1; y1), OM2 (x2; y2).
¡¡! ¡¡!
Вiдмiтимо, що з рiвностi (1.20) ма¹мо j M1M j = j¸jj MM2 j, çâiäêè
|
¡¡! |
|
|
|
|
|
¸ |
= |
j M1M j |
|
= |
M1M |
: |
|
|
|||||
j j |
¡¡! |
|
M2M |
|
||
|
|
j MM2 j |
|
|
|
|
(1.22)
¡¡!
OM
(1.23)
Приклад. В точках A(x1; y1), B(x2; y2) зосередженi маси m1, m2. Знайти координати центра ваги системи двох матерiальних точок A i B.
Розв'язання. Нехай M(x; y) ¹ центр ваги матерiальних двох точок A i B. Тодi, очевидно, M ¹ внутрiшньою точкою вiдрiзка AB, а тому дiлить його у вiдношеннi ¸ > 0. З курсу фiзики вiдомо, що m1 ¢ AM = m2 ¢ BM. Враховуючи тепер формулу (1.23), ми отриму¹мо
¸ = j¸j = AM = m2 : BM m1
Отже, згiдно (2.3) отриму¹мо
|
|
m2 |
|
|
|
m1x1 + m2x2 |
|
m2 |
|
m1y1 + m2y2 |
|
|||
x = |
x1 + m1 x2 |
= |
; y = |
y1 + m1 y2 |
= |
: |
||||||||
|
1 + m2 |
|
|
|
m1 + m2 |
1 + m2 |
|
m1 + m2 |
||||||
|
|
m1 |
|
|
|
|
|
|
|
m1 |
|
|
|
|
Таким чином, M( |
m1x1+m2x2 |
; |
m1y1+m2y2 |
).11 |
|
|
|
|
|
¤ |
||||
|
m1+m2 |
|
m1+m2 |
|
|
|
|
|
||||||
11 Доведiть самостiйно, що координати центра ваги M(x; y) трьох матерiальних точок A(x1; y1), B(x2; y2),
C(x3; y3) вiдповiдно з масами m1, m2, m3 |
знаходяться за наступними формулами: x = m1x1+m2x2+m3x3 |
y = m1y1+m2y2+m3y3 : |
m1+m2+m3 , |
m1+m2+m3 |
|
22

Можна показати, що координати центра ваги M(x; y) |
системи n матерiальних точок |
M1(x1; y1); M2(x2; y2); : : : ; Mn(xn; yn) вiдповiдно з масами |
m1; m2; : : : ; mn знаходяться за |
формулами:
x = m1x1 + m2x2 + ¢ ¢ ¢ + mnxn ; y = m1y1 + m2y2 + ¢ ¢ ¢ + mnyn : |
|
m1 + m2 + ¢ ¢ ¢ + mn |
m1 + m2 + ¢ ¢ ¢ + mn |
2 Орi¹нтацiя площини
Матриця переходу вiд одного базиса до iншого. Властивостi визнач- никiв матриць переходу. Вiдношення однаково¨ орi¹нтовностi базисiв. Орi¹нтацiя векторного простору та площини. Кут мiж векторами на орi¹нтованiй площинi.
Нехай на площинi задана афiнна система координат O~e1~e2 i L ¹ множина всiх векторiв |
||||
|
|
|
~ |
~ |
паралельних цiй площинi. Розглянемо два базиси A = (~a1;~a2) i B = (b1 |
; b2) векторного |
|||
простору L. Розкладемо кожен вектор базису B за векторами базису A: |
|
|||
|
|
~ |
= c11~a1 + c21~a2; |
|
|
|
b1 |
|
|
|
|
~ |
= c12~a1 + c22~a2: |
(1.24) |
Матрицю µ c21 |
|
b2 |
||
c22 |
¶, стовпцями яко¨ ¹ координати векторiв ~b1, ~b2 в базисi A, будемо |
|||
c11 |
c12 |
|
|
|
називати матрицею переходу вiд базису A до базису B. Визначник цi¹¨ матрицi12 ми будемо
|
|
|
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
позначати через AjB àáî (~a1;~a2)j(b1; b2), тобто |
|
¯ |
|
|
|
|
¯: |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
AjB = (~a1;~a2)j(~b1;~b2) = |
c11 |
|
c12 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
c21 |
|
c22 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
Оскiльки вектори |
|
|
|
|
|
|
|
¯ |
|
|
|
|
¯ |
|
A B = 0. |
|
|
|
|
|||||
|
|
|
~b1, ~b2 лiнiйно незалежнi, то, очевидно,¯ |
визначник¯ |
|
|
|
|
||||||||||||||||
Властивостi визначникiв матриць переходу: |
|
|
|
|
|
j |
6 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1±: |
Для довiльного базиса A = (~a1; a~2) справедлива рiвнiсть AjA = 1. |
|
|
|
|
|
|
|||||||||||||||||
|
Доведення. Дiйсно, оскiльки ~a1 = 1~a1 + 0~a2 i ~a2 = 0~a1 + 1~a2 |
, òî AjA = ¯ |
1 |
0 |
¯ |
= 1. |
||||||||||||||||||
|
0 |
1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
2±: |
Для довiльних трьох базисiв A = (~a1; a~2), B = (~b1; b~2), C = (~c1; c~2) викону¹ться¯ ¯ ðiâíiñòü |
|||||||||||||||||||||||
|
|
|
|
|
|
(AjB)(BjC) = AjC: |
|
|
|
|
|
|
|
|
(1.25) |
|||||||||
|
|
|
~ |
= c11~a1 |
+ c21~a2; |
|
~c1 |
|
|
|
~ |
|
|
~ |
; |
|
|
|
|
|
|
|
||
|
|
|
b1 |
|
= d11b1 |
+ d21b2 |
|
|
|
|
|
|
|
|||||||||||
|
Доведення. Нехай ~ |
= c12~a1 |
+ c22~a2; |
|
i ~c2 |
|
|
|
~ |
|
|
~ |
: |
Пiдставляючи значення |
||||||||||
|
|
|
b2 |
|
= d12b1 |
+ d22b2 |
||||||||||||||||||
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
; b2 в другу систему рiвностей, ми отрима¹мо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
~c1 = d11(c11~a1 + c21~a2) + d21(c12~a1 + c22~a2); |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
~c2 = d12(c11~a1 + c21~a2) + d22(c12~a1 + c22~a2): |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
¯ |
c11 |
c12 |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
||
12 Нагада¹мо, що визначником другого порядку |
назива¹ться число, яке записано у виглядi |
|||||||||||||||||||||||
c21 |
c22 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
наступним правилом: |
¯ |
c11 |
|
c12 |
¯ |
= c11c22 ¡ |
||||||
таблицi з двома рядками i двома стовпцями, що обчислю¹ться¯ |
ç௠|
c21 |
|
c22 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
¯ |
|
|
23

Розкриваючи тепер дужки i групуючи члени при ~a1;~a2, ми будемо мати:
~c1 = (d11c11 + d21c12)~a1 + (d11c21 + d21c22)~a2; ~c2 = (d12c11 + d22c12)~a1 + (d12c21 + d22c22)~a2:
Таким чином, |
¯ |
d11c21 + d21c22 d12c21 + d22c22 |
¯: |
|
|||||||||||
AjC = |
|
||||||||||||||
|
¯ |
d11c11 |
+ d21c12 |
d12c11 + d22c12 |
¯ |
|
|||||||||
|
¯ |
d¯ |
|
||||||||||||
Враховуючи тепер, що A B |
|
|
c |
|
c |
|
|
|
B C = |
|
d |
|
|
||
¯= |
¯ |
|
11 |
|
12 |
¯ |
i |
¯ |
|
11 |
¯12 |
¯, ми безпосередньою |
|||
j |
|
|
c21 |
c22 |
j |
d21 |
d22 |
||||||||
|
|
|
¯ |
|
|
|
|
¯ |
|
|
¯ |
|
|
|
¯ |
перевiркою перекону¹мося в справедливостi¯ ¯ |
рiвностi (1.25)¯ . |
|
¯ |
||||||||||||
|
|
|
¯ |
|
|
|
|
¯ |
|
|
¯ |
|
|
|
¯ |
3±: Для довiльних двох базисiв A, B викону¹ться рiвнiсть (AjB)(BjA) = 1.
Доведення. Дана рiвнiсть виплива¹ з перших двох властивостей 1± i 2± визначникiв матрицi переходу. 

Нехай B ¹ множина всiх базисiв векторного простору L. Введемо на B бiнарне вiдношення ¢ однаково¨ орi¹нтацi¨ базисiв за допомогою наступного означення.
Означення 1.14. Будемо казати, що базиси A; B 2 B однаково орi¹нтованi (це познача¹ться як A¢B), ÿêùî AjB > 0.
Теорема 1.12. Вiдношення ¢ ¹ вiдношенням еквiвалентностi на множинi всiх базисiв B.
Доведення. Для довiльного базиса A 2 B за властивiстю 1± ìà¹ìî AjA = 1 > 0, òîìó A¢A. Îòæå, ¢ ¹ рефлексивне вiдношення.
Нехай для базисiв A; B 2 B ìà¹ìî A¢B, тобто AjB > 0, тому за властивiстю 3± íó¹òüñÿ íåðiâíiñòü BjA = > 0. Îòæå, B¢A. Таким чином, вiдношення ¢ симетричне.
Доведемо нарештi транзитивнiсть вiдношення ¢. Нехай базиси A; B; C 2 B задовольняють умови A¢B i B¢C, тобто AjB > 0 i BjC > 0. Згiдно властивостi 2± ìà¹ìî AjC = (AjB)(BjC) > 0, òîìó A¢C. Отже, транзитивнiсть доведена. 

Нехай B=¢ ¹ фактор-множина13 множини всiх базисiв B по вiдношенню ¢. Доведемо,
що вона мiстить всього два елементи. Розглянемо¯ базиси¯ A = (~a1;~a2) i B = (~a2;~a1). Îñêiëüêè
~a2 = 0~a1 + 1~a2 i ~a1 = 1~a1 + 0~a2, òî AjB = ¯¯¯ 01 10 ¯¯¯ = ¡1 < 0. Îòæå, (A; B) 62¢, тобто
базиси A; B не мають однаково¨ орi¹нтацi¨. Позначимо через KA i KB класи еквiвалентностi вiдношення ¢, якi мiстять вiдповiдно базиси A i B. ßñíî, ùî KA 6= KB, iнакше базиси A i B
мали б однакову орi¹нтацiю. Розглянемо довiльний базис C = (~c1;~c2) 2 B. Згiдно властивостi 2± ìà¹ìî AjC = (AjB)(BjC) = (¡1)(BjC), тому визначники AjC i BjC мають рiзнi знаки.
Îòæå, àáî A¢C, àáî B¢C. Îòæå, àáî C 2 KA, àáî C 2 KB. Останн¹ означа¹, що B=¢ мiстить всього два елементи.
Означення 1.15. Кожний елемент фактор-множини B=¢ назива¹ться îði¹íòàöi¹þ векторного простору L.
13 тобто множина всiх класiв еквiвалентностi вiдношення ¢.
24
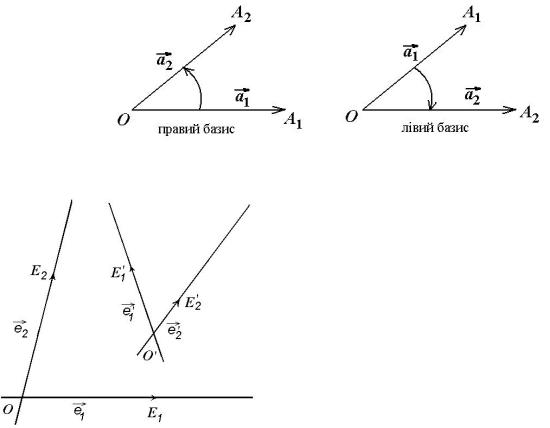
Один з елементiв множини B=¢ називають додатною орi¹нтацi¹ю, а iнший вiд'¹мною. В геометрi¨ на площинi розрiзняють два типи базисiв правий i лiвий. Якщо A = (~a1;~a2) 2 B
¡¡! |
¡¡! |
i ~a1 =OA1, ~a2 |
=OA2, äå O; A1; A2 точки площини, то A називають правим базисом, |
якщо поворот навколо точки O вiд вектора ~a1 до вектора ~a2 викону¹ться проти руху
годинниково¨ стрiлки, iнакше даний базис називають лiвим (дивись рисунок нижче на стор. 25). На практицi домовились за додатну орi¹нтацiю завжди вибирати правий базис. Площина назива¹ться орi¹нтованою, якщо орi¹нтована0 0 множина0 0 всiх векторiв цi¹¨ площини.
Два афiнних репери R = (O;~e1;~e2) i R = (O ;~e 1;~e 2) кажуть, що вони однаково орi¹нтованi (протилежно орi¹нтованi), якщо базиси (~e1;~e2) i (~e 01;~e 02) однаково орi¹нтованi
(протилежно орi¹нтованi). Зокрема, репер R = (O;~e1;~e2) називають додатно орi¹нтованим, якщо базис (~e1;~e2) належить додатнiй орi¹нтацi¨.
Для кращого вiзуального сприйняття афiнний репер R = (O;~e1;~e2) будемо називати правим,
коли направленi вiдрiзки |
OE1 |
i |
OE2 |
розташованi як великий i вказiвний палець право¨ руки |
|||||||||
|
|
|
|
|
|
(якщо дивитись на розкриту долоню), а |
|||||||
|
|
|
|
|
|
афiнний репер |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
R0 = (O0;~e 10 ;~e 20 ) |
|||
|
|
|
|
|
|
будемо |
називати лiвим, коли ж направленi |
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
âiäðiçêè OE10 i |
|
OE20 розташованi як великий |
|||||
|
|
|
|
|
|
i вказiвний палець лiво¨ руки (якщо дивитись |
|||||||
|
|
|
|
|
|
на розкриту долоню). Як правило, орi¹нтацiю |
|||||||
|
|
|
|
|
|
площини обирають так, щоб додатна орi¹нтацiя |
|||||||
|
|
|
|
|
|
була правою. Отож, система координат викону¹ |
|||||||
|
|
|
|
|
|
ще одне завдання, а саме, зада¹ орi¹нтацiю |
|||||||
~ |
|
|
|
|
|
площини. |
|
вважа¹ться першим, а ~ |
|||||
ненульовi вектори, серед яких вектор ~a |
|||||||||||||
Нехай ~a; b |
|
|
|
|
b другим. |
||||||||
~ |
|
|
|
|
|
|
~ |
|
~ |
||||
ßêùî ~a , b, то направленим кутом мiж векторами ~a; b назива¹ться величина (~a; b), ÿêùî |
|||||||||||||
~ |
~ |
|
~ |
|
|
|
|
|
|
||||
базис ~a; b правий i величина ¡(~a; b), коли базис ~a; b лiвий. Направлений кут надалi будемо |
|||||||||||||
направлених |
c |
c |
|
|
|
|
|
|
|||||
|
~ |
|
|
|
|
~ |
|
|
|
|
|
|
|
позначати як (~a; b). Очевидно, що ¡¼ |
< (~a; b) 6 ¼. Вiдмiтимо три очевиднi властивостi |
||||||||||||
êóòiâ:
1± ( c ) |
~ |
¡ c |
~ |
|
~ |
|
~ |
|
|||
|
: |
~ |
= |
|
~ |
|
|
|
|
|
|
|
~a; b |
|
(b;~a); |
|
cos( c ) = cos( c ) |
|
|||||
2± |
|
sin( c ) = ¡ sin( c ) |
|
||||||||
|
: |
~a; b |
|
|
b;~a , |
~a; b |
|
b;~a |
; |
||
3±: |
sin ³(~a; |
~b) + (~b;~c)´ |
= sin(~a;~c), |
cos |
³(~a;~b) + (~b;~c)´ |
||||||
|
|
|
c |
|
c |
|
c |
|
c |
c |
|
c
= cos(~a;~c).
25

Теорема 1.13. Координати (a1; a2) довiльного ненульового вектора ~a в ортонормованому |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
базисi ~ ~ |
обчислюються за формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
i; j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 = j~aj cos(i;~a); |
|
|
|
a2 = j~aj sin(i;~a): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Доведення. Помноживши рiвнiсть |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
~ скалярно на вектор |
~i |
, ми отрима¹мо |
~i~a = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
логiчно доводимо, що a2 |
= ~a |
|
|
|
|
|
|
~a = ac1i + a2j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
j j |
|
c |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
cos(~j;~a). Îñêiëüêè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j jj j |
|
|
|
c |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
~~ |
|
~~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~~ |
= 1 |
i ~~ |
= 0 |
. Îòæå, |
|
a1 |
|
|
|
|
|
~ |
|
|
|
= |
~ |
|
|
~a |
|
|
~ |
|
|
|
|
|
|
|
|
~ |
|
. Àíà- |
||||||||||||||||||||||||||||||||||||||||||
a1ii + a2ij |
|
= a1, îñêiëüêè |
ii |
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
= i~a |
i |
|
|
cos(i;~a) = ~a |
cos(i;~a) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
j |
j |
|
|
|
|
c |
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
¼ |
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
c |
cos(~j;~a) = cos ³(~j;~i) + (~i;~a)´ = cos |
|
³(~i;~a) ¡ |
2 |
|
´ = sin(~i;~a); |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Íàñëiäîê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~a0 |
â |
|
ортонормованому |
|
правому |
|
базисi |
|
~i;~j |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
òî |
|
|
|
|
|
|
|
|
~ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
a2 |
= j~aj sin(i;~a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1.5. Одиничний |
|
|
вектор |
|
|
|
, ~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì๠|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
координати ~a0 |
³cos(~i;~a |
0); sin(~i;~a |
0)´. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Íàñëiäîê 1.6. Якщо вектори ~a(a1; a2) |
|
|
|
b(b1; b2) |
|
|
заданi координатами в ортонормованому |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
правому базисi ~ ~ |
, то мають мiсце такi рiвностi: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i; j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
a1b1 + a2b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.26) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~a; b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j~ajj~bj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos( c ) = |
|
|
|
|
|
|
|
|
|
; |
|
|
¯ |
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
a1b2 |
|
|
|
a2b1 |
|
|
|
|
|
|
a2 |
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.27) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
a1 |
|
|
b1 |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~a |
|
~b |
|
|
|
|
|
|
|
|
|
|
~a |
~b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
j |
jj |
|
j |
|
|
|
|
|
|
|
|
|
|
¯ |
|
j |
|
|
jj |
|
j |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin(~a; b) = |
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
= |
|
|
¯ |
|
|
|
|
|
|
|
|
¯ |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
cos |
|
= cos ( |
|
|
|
) + ( |
|
|
|
) |
|
= cos |
|
( |
|
|
|
|
) ¡ ( |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
2 ¡ 1c |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
||||||||||||||||||||||||||||||||||||||
Доведення. Введемо такi позначення: |
' |
|
= |
|
|
|
|
|
~ |
|
|
|
, |
|
'1 = |
|
~ |
|
|
|
|
, |
|
'2 |
= |
|
|
|
~ ~ |
|
, тодi матимемо |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
теоремою |
|
³ |
|
|
~ |
|
|
|
~ |
~ |
´ |
|
|
|
|
|
|
|
³ |
~ |
~ |
|
|
|
|
|
|
~ |
|
|
|
|
´ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
' |
|
|
|
|
|
|
~a; i |
|
|
|
|
i; b |
|
|
|
|
|
|
|
|
|
|
|
|
i; b |
|
|
|
|
|
|
|
i;~a |
|
|
|
= cos(' |
|
|
|
|
' ) = cos ' |
|
cos ' |
+ sin ' |
|
sin ' . Çà |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1.13 ìà¹ìî: |
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
, |
a |
|
|
|
|
|
|
|
|
~a |
|
|
|
|
|
' |
|
|
, |
b |
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
' |
. Îòæå, |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
ca1 |
= ~a cos |
c1 |
|
|
|
2 |
|
=c |
|
sin |
|
1 |
|
|
|
|
1 |
= |
|
b |
cos '2 |
|
b2 = |
j j |
sin |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos '1 |
= |
|
a1 |
|
; |
|
sin '1 |
= |
|
|
a2 |
|
; |
|
|
|
cos '2 |
|
= |
|
b1 |
|
; |
|
|
sin '2 = |
|
b2 |
: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j~aj |
|
|
|
|
j~aj |
|
|
|
|
|
|
~ |
|
|
|
~ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jbj |
|
|
|
|
|
|
|
|
|
|
jbj |
|
|
|
|
|
|
|
|
|
||||||||||||||||
Таким чином, cos ' = |
|
a1 |
|
b1 |
|
+ |
a2 |
|
|
b2 |
|
|
|
= |
a1b1 + a2b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
~ |
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j~aj |
|
|
|
|
|
|
j~aj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~a |
|
~ |
|
|
|
|
|
|
|
|
. Рiвнiсть (1.26) доведена. Далi ма¹мо |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
j |
|
|
|
|
j |
b |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
j |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
jj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
sin ' = sin |
|
³(~a; i) + (i; b)´ |
= sin |
|
³(i; b) ¡( a |
|
|
)´b |
= sin('2 ¡ 1) = sin |
|
|
2 cos |
|
|
|
1 ¡cos '2 sin |
|
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
c |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
c1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
~ |
~ |
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
|
' |
|
|
|
' |
|
|
|
|
|
|
|
' , òîìó |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
i;~a |
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
b2 a1 |
|
|
|
b1 |
a2 |
|
|
|
a1b2 |
|
|
|
a2b1 |
|
|
|
|
|
a2 b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
sin ' = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
¡ |
|
|
|
|
|
= |
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
~b |
|
|
|
~a |
¡ |
|
~b |
|
|
~a |
|
|
|
|
|
|
|
~a ~b |
j |
|
|
|
¯ |
|
|
|
~a |
~b |
j |
|
¯. Рiвнiсть (1.27) доведена також. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
j |
j j j |
|
|
j |
j j j |
|
|
|
|
|
j jj |
|
|
|
|
|
|
|
¯ |
|
|
j jj |
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
3 Перетворення афiнних координат. Полярнi координати
Перетворення афiнних координат точок. Перенесення початку координат. Замiна координатних векторiв. Формули перетворення прямокутних координат. Полярна система координат та ¨¨ зв'язок з прямокутною декартовою системою координат.
26
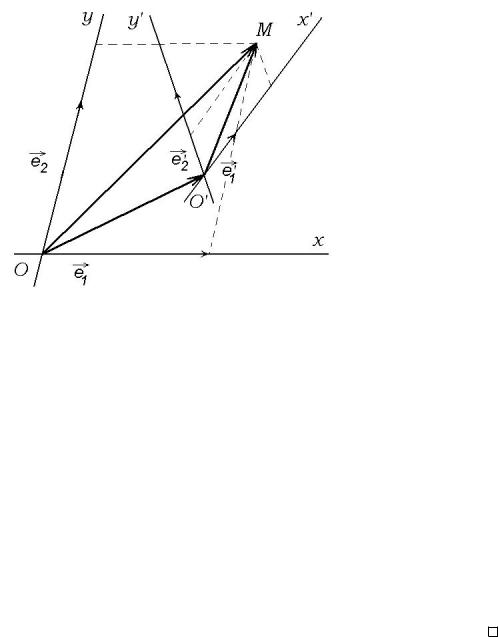
Нехай на площинi задано двi афiннi системи координат (O;~e1;~e2) i (O0;~e 01;~e 02) (див. рисунок на стор. 27 ). Заради зручностi першу назвемо старою, а другу0 0 новою. Вiзьмемо точку M, i нехай ¨¨ координати у старiй системi (x; y), à ó íîâié (x ; y ). Необхiдно старi
координати (x; y) довiльно¨ точки M виразити через ¨¨ новi координати (x0; y0). Нехай вектори
OO 0 |
;~e |
;~e |
0 |
~e |
;~e |
2) |
мають подання: |
|
|
|
|
|
|
|
|
||||
¡¡! |
0 |
|
у базисi ( 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OO 0 |
|
x ~e |
+ y0~e2; |
0 |
= |
c |
11 |
~e |
1 |
+ c21~e2; |
0 |
= c12~e1 + c22~e2: |
(1.28) |
||
|
|
|
|
¡¡! = |
|
0 1 |
~e 1 |
|
|
~e 2 |
|
||||||||
Теорема 1.14. Координати (x; y) точки M у старiй системi координат виражаються через ¨¨ координати (x0; y0) у новiй системi за формулами
x = c11x0 + c12y0 + x0; y = c21x0 + c22y0 + y0:
Доведення. Виходячи з рiвностей
OM = ¡¡! |
+ ¡¡¡! |
¡¡! |
= |
|
1 |
+ |
2 |
|
|
¡¡! |
OO 0 |
O 0M; |
|
x~e |
|
; |
|||
|
OM |
|
|
|
y~e |
||||
(1.29)
¡¡¡! |
= |
1 + |
2 |
O 0M |
|
x0~e 0 |
y0~e 0 |
i враховуючи подання (1.28), ма¹мо
x~e1 + y~e2 = (x0~e1 + y0~e2) + (x0~e 01 + y0~e 02) =
=x0~e1 + y0~e2 + x0(c11~e1 + c21~e2) + y0(c12~e1 + c22~e2) =
=(c11x0 + c12y0 + x0)~e1 + (c21x0 + c22y0 + y0)~e2:
А оскiльки вектори ~e1 i ~e2 лiнiйно незалежнi, то звiдси дiста¹мо формули (1.29).
Надалi формули (1.29) ми називатимемо формулами перетворення афiнних координат. |
|||||
Неважко бачити, що матриця |
µ c21 |
c22 |
¶ |
êîåôiöi¹íòiâ ïðè x0; y0 |
|
|
c11 |
c12 |
|
|
â íèõ ¹ íå ùî iíøå, ÿê ìàò- |
риця переходу вiд базиса (~e1;~e2) до базиса (~e 01;~e 02). Розглянемо тепер два окремих випадки даних формул:
27
а) Перенесення початку координат. В цьому випадку початки координат старо¨ i ново¨ |
|||||||
систем координат рiзнi, тобто O = O 0 |
, а базиснi вектори спiвпадають, тобто ~e |
= ~e 0 |
;~e |
= ~e 0 |
|||
6 |
|
0 |
1 |
1 |
1 |
2 |
2. |
Тодi матриця переходу, очевидно, ма¹ вигляд µ |
¶, тому формули (1.29) будуть такi: |
||||||
|
|
1 |
0 |
|
|
|
|
|
x = x0 + x0; |
|
|
|
|
|
|
|
y = y0 + y0: |
|
|
|
|
(1.30) |
|
б) Замiна координатних векторiв. В0 даному випадку початки координат спiвпадають, а базиснi вектори рiзнi. Оскiльки O = O , òî x0 = 0, y0 = 0. Отже формули (1.29) будуть такi:
x = c11x0 + c12y0; |
|
y = c21x0 + c22y0: |
(1.31) |
Часто нам доводиться мати справу з прямокутними декартовими системами координат, |
||
тому далi ми знайдемо формули перетворення прямокутних координат. Нехай |
~ ~ |
i |
(O 0;~i 0;~j 0) ¹ двi прямокутнi системи координат. Можливi такi два випадки: |
(O; i; j ) |
|
|
|
|
а) Системи (O;~i;~j ) i (O 0;~i 0;~j 0) орi¹нтованi однаково, тобто вони обидвi правi. Нехай |
|||||||||
® = (~i;~i 0), òîäi çà íàñëiäêîì 1.5 ìà¹ìî ~i 0(cos ®; sin ®); |
~j 0³cos(~i;~j 0); sin(~i;~j |
0)´: Àëå |
|||||||
d |
|
|
|
¼ |
d |
d |
|||
cos(~i;~j 0) = cos |
³(~i;~i 0) + (~i[0;~j 0)´ |
= cos |
³® + |
|
|
´ = ¡ sin ®; |
|
||
2 |
|
||||||||
d |
d |
= sin ³® + |
¼ |
|
|
|
|
||
sin(~i;~j 0) = sin ³(~i;~i 0) + (~i[0;~j 0)´ |
2 ´ = cos ®: |
|
|||||||
d |
d |
|
|
|
|
|
|
µ sin ® |
¡cos ® ¶, òîìó |
Отже, матриця переходу вiд старого базиса до нового ма¹ вид |
|||||||||
|
|
|
|
|
|
|
|
cos ® |
sin ® |
формули перетворення в даному випадку будуть такi:
x = x0 cos ® ¡ y0 sin ® + x0; y = x0 sin ® + y0 cos ® + y0:
Вiдмiтимо, що визначник матрицi переходу дорiвню¹ одиницi, тобто
(1.32)
¯¯
¯¯ cos ® ¡ sin ® ¯¯
¯sin ® cos ® ¯ = 1.
ßêùî O = O 0, то формули (1.32) ¹ формули повороту системи координат навколо початку координат O íà êóò ®:
|
|
|
x = x0 cos ® ¡ y0 sin ®; |
|
|
|
|
|
|
|
|
y = x0 sin ® + y0 cos ®: |
|
|
|
|
(1.33) |
б) Системи (O;~i;~j ) i |
(O 0;~i 0;~j 0) орi¹нтованi протилежно, |
тобто (O;~i;~j ) ма¹ праву |
||||||
|
|
|
[ |
¼ |
|
|
|
|
îði¹íòàöiþ, à (O 0;~i 0;~j 0) лiву. В цьому випадку (~i 0;~j 0) = ¡ |
2 , òîìó |
= ¡ cos ®: |
||||||
cos(~i;~j 0) = cos ³® ¡ 2 |
´ = sin ®; sin(~i;~j 0) = sin ³® ¡ |
2 |
´ |
|||||
d |
|
¼ |
d |
|
¼ |
|
|
|
Отже, матриця переходу вiд старого базиса до нового ма¹ вид |
µ sin ® |
¡ cos ® ¶, òîìó |
||||||
|
|
|
|
|
|
|
cos ® |
sin ® |
формули перетворення в даному випадку будуть такi: |
|
|
|
|
|
|||
|
|
x = x0 cos ® + y0 sin ® + x0; |
|
|
|
|
|
|
|
|
y = x0 sin ® ¡ y0 cos ® + y0: |
|
|
|
|
(1.34) |
|
28
Вiдмiтимо, що визначник матрицi переходу дорiвню¹ одиницi, тобто |
¯ |
sin ® |
¡ |
cos ® |
¯ |
= ¡1. |
|
|
¯ |
cos ® |
sin ® |
¯ |
|
||
Об'¹днуючи тепер формули (1.32) i (1.34) разом, ми отриму¹мо,¯ |
так званi, формули¯ |
||||||
перетворення прямокутних координат: |
¯ |
|
|
|
|
¯ |
|
x = x0 cos ® ¡ "y0 sin ® + x0; |
|
|
|
|
|
|
|
y = x0 sin ® + "y0 cos ® + y0; |
|
|
|
|
|
|
(1.35) |
äå " = §1, причому знак (+) береться, коли системи координат орi¹нтованi однаково, а (¡)
у випадку протилежно¨ орi¹нтацi¨.
На завершення розглянемо найпростiший варiант координат на площинi полярну систему координат. Будемо вважати, що площина орi¹нтована, а отже, вiдомо, яким кутам припису¹ться додатна мiра (як правило, проти ходу годинниково¨ стрiлки). Вiзьмемо на площинi промiнь OP i вiдкладемо на ньому одиничний вiдрiзок OA. Ïðîìiíü OP називають
полярною вiссю, а його початок O полюсом. Вiзьмемо довiльну точку M площини, яка не збiга¹ться з полюсом. Нехай ½ = d(O; M), à ' величина кута мiж променями OP i OM. Очевидно, що числа ½ i ' визначають положення точки на площинi, причому рiзним точкам вiдповiдають рiзнi пари чисел (½; ') з множини (0; +1) £ [0; 2¼). Якщо тепер взяти будь-яку пару (½; ') з множини (0; +1) £ [0; 2¼), то досить провести промiнь пiд кутом ' до променя OP (вiдлiк проти ходу годинниково¨ стрiлки) i на ньому вiдкласти вiдрiзок OM довжини ½. Точка M якраз i буде визначатись парою чисел (½; '). Якщо точка M збiга¹ться з полюсом, то вона визнача¹ться числом ½ = 0 (' невизначено). Таким чином, мiж точками площини i множиною (0; +1) £ [0; 2¼) встановлена вза¹мно однозначна вiдповiднiсть, тобто задана система координат, яка носить назву полярно¨, а пари чисел (½; '), äå 0 < ½ < +1, 0 6 ' < 2¼, називають полярними координатами (для полюса одна координата ½ = 0).
Координатними лiнiями тут ¹ кола i прямi (двi сiм'¨ вза¹мно ортогональних лiнiй). |
|
|
|||||||||||||||||||
|
|
До кожно¨ полярно¨ системи координат можна при¹днати |
|||||||||||||||||||
|
|
прямокутну декартову |
~ ~ |
, початок яко¨ ¹ полюс |
O |
, |
|||||||||||||||
|
|
i |
i |
= ¡! |
|
|
|
(O; i; j) |
|
|
|
= 0 |
|
|
|
||||||
|
|
îðò ~ |
|
|
OA |
. ßêùî |
точка |
M |
( |
M |
6 |
) |
ма¹ полярнi |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координати (½; '), то очевидно, що ¨¨ координати (x; y) |
|||||||||||||||||||
|
|
у при¹днанiй прямокутнiй декартовiй системi координат |
|||||||||||||||||||
|
|
подаються через них так: |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x = ½ cos '; y = ½ sin ': |
|
|
|
|
||||||||||
|
|
Навпаки, якщо (x; y) |
координати точки M ó ïðè¹äíàíié |
||||||||||||||||||
|
|
прямокутнiй декартовiй системi координат |
~ ~ , òî ¨¨ |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(O; i; j) |
|
|
½ = p |
|
полярнi координати (½; ') подаються через них так: |
|
|
|||||||||||||||||
|
; |
cos ' = |
|
x |
; |
sin ' = |
|
y |
: |
|
|
|
|
|
|||||||
x2 + y2 |
|
|
|
|
|
||||||||||||||||
p |
|
p |
|
|
|
|
|
|
|||||||||||||
x2 + y2 |
x2 + y2 |
|
|
|
|
|
|||||||||||||||
29

1.3 Пряма лiнiя на площинi
1 Рiвняння прямо¨ на площинi
Параметричнi рiвняння прямо¨. Рiвняння прямо¨, яке визнача¹ться точкою i напрямним вектором. Канонiчне рiвняння прямо¨. Рiвняння прямо¨, яка проходить через двi точки. Рiвняння прямо¨ у вiдрiзках. Рiвняння прямо¨ з кутовим коефiцi¹нтом.
Нехай l довiльна пряма на площинi. Будь-який ненульовий вектор ~a, паралельний
ïðÿìié l, будемо називати напрямним вектором цi¹¨ прямо¨. Якщо M0 ¹ точка цi¹¨ прямо¨, |
|||
|
|
|
¡¡¡! |
то точка M буде належати прямiй l тодi i тiльки тодi, коли вектори M0M i ~a колiнеарнi, |
|||
тобто коли iсну¹ t |
2 R |
¡¡¡! |
|
òàêå, ùî M0M = t~a. Тодi векторне рiвняння |
|
||
|
¡¡¡! |
|
|
|
|
(1.36) |
|
|
|
M0M = t~a; |
|
äå t 2 R, зада¹ пряму l.
Нехай на цiй площинi обрано деяку афiнну систему координат (O;~e1;~e2), i нехай точки M0 i M прямо¨ мають координати: M0(x0; y0), M(x; y), а вектор ~a у базисi (~e1;~e2) ïîäà¹òüñÿ
у виглядi |
|
|
|
|
|
~a = a1~e1 |
+ a2~e2: |
|
|
||||||
Îñêiëüêè ¡¡¡! |
¡ |
|
¡ |
|
|
|
|
||||||||
|
0 |
|
2 |
|
|
|
|
|
|
|
|||||
|
|
M0M = (x |
|
x0)~e1 + (y |
|
y |
)~e , то рiвнiсть (1.36) можна записати у виглядi |
|
|
||||||
|
|
|
|
(x ¡ x0)~e1 + (y ¡ y0)~e2 = ta1~e1 + ta2~e2: |
|
|
|||||||||
А оскiльки вектори ~e1 i ~e2 лiнiйно незалежнi, то з останньо¨ рiвностi виплива¹, що |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x = x0 + a1t; |
|
|
|
||||
|
|
|
|
|
|
|
|
y = y0 + a2t; |
|
(1.37) |
|||||
äå t |
2 R |
|
|
|
|
|
|
|
|
|
|
|
¡¡¡! k |
~a, òî |
|
|
, тобто пряма l зада¹ться параметрично рiвняннями (1.37). Оскiльки M0M |
|
|||||||||||||
за теоремою 1.11 ма¹мо |
|
|
¯ |
|
¡ y0 |
|
¯ = 0 |
|
|
||||||
|
|
|
|
|
|
|
y |
a2 |
(1.38) |
||||||
|
|
|
|
|
|
|
¯ |
x |
¡ |
a1 |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
ó òàêié ôîðìi: |
|
|
||
або, обчислюючи визначник, це рiвняння¯ |
записують¯ |
|
|
||||||||||||
|
|
|
|
|
|
|
¯ |
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
a2(x ¡ x0) ¡ a1(y ¡ y0) = 0: |
(1.39) |
|||||||||
Рiвняння (1.38) i (1.39) називають рiвнянням прямо¨, що визнача¹ться точкою i напрямним вектором. Якщо a1 =6 0 i a2 =6 0, то рiвняння (1.39) часто записують у такiй формi:
|
|
|
|
x ¡ x0 |
= |
y ¡ y0 |
; |
|
|
(1.40) |
|||
|
|
|
|
a1 |
|
|
|
a2 |
|
|
|
|
|
яке назива¹ться канонiчним рiвнянням прямо¨. |
|
|
|
|
|
; y2), тодi за напрямний |
|||||||
Нехай пряма проходить через двi даних точки M1(x1; y1) i M2(x2 |
|||||||||||||
вектор прямо¨ можна взяти вектор |
¡¡¡¡! |
|
¡ |
|
|
|
¡ |
y1). Пiдставляючи тепер в (1.38) |
|||||
|
1 |
|
M1M2(x2 |
|
|
x1 |
; y2 |
|
|||||
|
¡¡¡¡! |
|
|
|
|
|
|
|
|
|
|||
координати точки M |
|
i вектора M1M2 замiсть координат точки M0 |
i вектора ~a âiäïîâiäíî, |
||||||||||
ми отрима¹мо рiвняння прямо¨, що визнача¹ться двома точками: |
(1.41) |
||||||||||||
|
|
¯ |
y |
¡ y1 |
y2 |
¡y1 |
¯ = 0: |
|
|||||
|
|
¯ |
|
¡ |
|
¡ |
|
¯ |
|
|
|
|
|
|
|
¯ |
x |
x1 |
x2 |
|
|
x1 |
¯ |
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
¯ |
|
|
|
|
30
