Prak_Geom1

äå a12 6= 0. Знайдемо головнi напрямки i вiзьмемо ¨х за напрямки нових осей координат.

~c

Координати одиничного вектора p~(cos ®; sin ®) головного напрямку (де ® = (i; p~))

задовольня¹ рiвняння (1.142), тобто (a22 ¡ a11) cos ® sin ® + a12(cos2 ® ¡ sin2 ®) = 0. Розкри¹мо дужки i запишемо пiсля перетворень дане рiвняння таким чином:

(a11 cos ® sin ® + a12 sin2 ®) ¡ (a21 cos2 ® + a22 cos ® sin ®) = 0; 26

звiдки, пiсля винесення за дужки sin ® i cos ®, ми отрима¹мо рiвняння

(a11 cos ® + a12 sin ®) sin ® ¡ (a21 cos ® + a22 sin ®) cos ® = 0;

яке у виглядi визначника другого порядку запишеться так:

Якщо подивитись на стовпцi отриманого визначника, як на координати деяких векторiв, то рiвнiсть (1.149) згiдно теореми 1.11 означатиме, що цi вектори колiнеарнi, а тому за теоремою про колiнеарнi вектори (див. стор. 11) знайдеться таке число ¸, що буде мати мiсце система

Розглядаючи дану однорiдну систему вiдносно невiдомих cos ® i sin ® ми бачимо, що вона ма¹ ненульовi розв'язки, оскiльки cos ® i sin ® одночасно не можуть дорiвнювати нулевi. Отже,

який вiдповiда¹ кореню ¸1. Пiдставивши ¸1 в перше рiвняння системи (1.151), ми отрима¹мо

26Нагада¹мо, що a12 = a21.

91

Пiдставивши значення x; y згiдно формул (1.154) в рiвняння (1.148), ми отрима¹мо рiвняння лiнi¨ ° в системi координат Ox0y0:

коефiцi¹нти якого знаходяться за такими формулами:

Виходячи з системи (1.150) формули (1.156) i (1.157) можна записати бiльш компактно, а саме:

a011 = a11 cos2 ® + 2a12 cos ® sin ® + a22 sin2 ® =

=(a11 cos ® + a12 sin ®) cos ® + (a21 cos ® + a22 sin ®) sin ® =

=¸1 cos2 ® + ¸1 sin2 ® = ¸1:

З рiвняння (1.161) шляхом перенесення початку координат в деяку точку O 0 отриму¹мо канонiчне рiвняння лiнi¨ °. ßêùî ° не ¹ параболою, то O 0 центр (або один з центрiв) лiнi¨ °; ÿêùî æ ° парабола, то O 0 ¨¨ вершина.

Таким чином, для того щоб звести рiвняння (1.148) лiнi¨ ° другого порядку до канонiчного виду i побудувати графiк, необхiдно виконати такi дi¨:

0 , оскiльки вектор ~ 0 ма¹ головний напрямок (див. стор. 89). 27Êîåôiöi¹íò a12 = 0 j

92

3.Обчислити коефiцi¹нти a010, a020 за формулами (1.158), (1.159) i записати рiвняння лiнi¨ ° у виглядi (1.161).

4.Перенесенням початку координат отримати канонiчне рiвняння лiнi¨ °.

~ 0~ 0

îñåé CX òà CY системи координат Ci j , äå C(1; 0) точка площини. Графiк даного елiпса матиме такий вигляд:

28Це означа¹, що ми виконали паралельне перенесення початку координат O 0 в точку C(1; 0). Таким чином,

~ 0~ 0.

ми отримали рiвняння дано¨ лiнi¨ в системi координат Ci j

93

5x2 + 8xy + 5y2 ¡ p2 x + p2 y ¡ 8 = 0:

94

Ðîçäië 2

Геометрiя в просторi: площини, прямi лiнi¨, поверхнi другого порядку

2.1Метод координат в просторi. Мiшаний та векторний добутки векторiв

1 Координати точок в просторi

Афiнна система координат в просторi. Координати точки в просторi. Дiлення вiдрiзка в заданому вiдношеннi. Прямокутна система координат в просторi. Довжина вiдрiзка.

Координатна система в просторi вводиться по аналогi¨ з системою координат на площинi (див. стор. 20). Вiзьмемо деяку точку O i довiльний базис ~e1; ~e2; ~e3 простору. Четвiрка,

яка склада¹ться з точки O i базиса ~e1; ~e2; ~e3 назива¹ться афiнною системою координат

абсцисою, y ординатою, а z аплiкатою точки M, при цьому пишуть: M(x; y; z). Таким чином, координатами точки M в системi координат O~e1~e2~e3 називаються числа x; y; z òàêi,

95

Дiлення вiдрiзка в заданому вiдношеннi в просторi визнача¹ться так саме, як i для випадку площини (див. означення 1.13), тому ми скориста¹мося мiркуваннями наведеними на сторiнцi 22. Отже, нехай в афiннiй системi координат ~e1; ~e2; ~e3 заданi точки сво¨ми

координатами: M1(x1; y1; z1), M2(x2; y2; z2), M(x; y; z), причому точка M дiлить направлений вiдрiзок M1M2 у вiдношеннi ¸. Тодi, як вiдмiчалось на сторiнцi 22, буде мати мiсце рiвнiсть

звiдки отриму¹мо афiннi координати точки подiлу M:

Якщо точка M дiлить даний вiдрiзок пополам, то ¸ = 1, а тому отриманi формули

2 Орi¹нтацiя простору

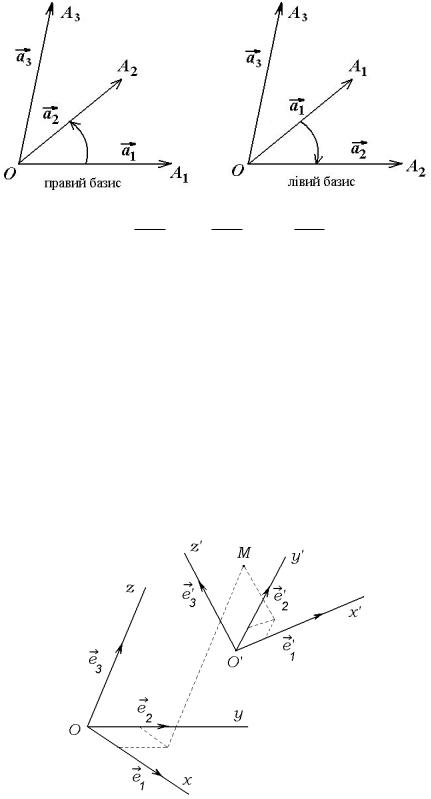
Ознака компланарностi трьох векторiв в координатнiй формi. Матриця переходу вiд одного базиса до iншого. Властивостi визначникiв матриць переходу. Вiдношення однаково¨ орi¹нтовностi базисiв. Орi¹нтацiя векторного простору. Правий i лiвий базиси в просторi.

Доведемо теорему про ознаку компланарностi трьох векторiв, заданих координатами.

, ~

Теорема 2.1. Для того щоб вектори ~a(a1; a2; a3) b(b1; b2; b3) i ~c(c1; c2; c3), якi заданi координатами в довiльному базисi ~e1, ~e2, ~e3, були компланарними, необхiдно i достатньо,

~

Доведення. Нехай вектори ~a; b;~c компланарнi, тодi за теоремою 1.6 про лiнiйну залежнiсть

трьох векторiв робимо висновок, що данi вектори лiнiйно залежнi. Це означа¹, що знайдуться такi числа ®; ¯; °, одночасно не рiвнi нулевi, такi, що

96

Запишемо рiвнiсть (2.6) в координатах:

Таким чином, стовпцi визначника ¢ в лiвiй частинi рiвностi (2.5) лiнiйно залежнi, тому, як вiдомо з курсу алгебри, такий визначник дорiвню¹ нулевi, тобто ¢ = 0. Îòæå, ðiâíiñòü (2.5)

викону¹ться.

Навпаки, якщо викону¹ться рiвнiсть (2.5), тодi стовпцi визначника ¢ лiнiйно залежнi, тобто система (2.7) однорiдних лiнiйних рiвнянь вiдносно ®; ¯; ° ма¹ ненульовi розв'язки. Помноживши рiвняння системи (2.7) вiдповiдно на ®; ¯; ° i додавши ¨х, ми отрима¹мо:

~

(®a1 + ¯b1 + °c1)® + (®a2 + ¯b2 + °c2 = 0)¯ + (®a3 + ¯b3 + °c3)° = 0;

звiдки, розкривши дужки i згрупувавши члени при ®; ¯; °, ми будемо мати:

~

®(a1~e1 + a2~e2 + a3~e3) + ¯(b1~e1 + b2~e2 + b3~e3) + °(c1~e1 + c2~e2 + c3~e3) = 0;

~

тобто викону¹ться рiвнiсть (2.6). Отже, вектори ~a; b;~c лiнiйно залежнi, а тому вони компланарнi.

Поняття орi¹нтацi¨ простору вводиться аналогiчно введенню орi¹нтацi¨ площини. Отже, нехай в просторi задана афiнна система координат O~e1~e2~e3 i V ¹ множина всiх векторiв в

переходу вiд базису A до базису B. Визначник цi¹¨ матрицi будемо позначати через AjB.

97

Оскiльки вектори ~ ~ ~

b1, b2, b3 лiнiйно незалежнi, то, очевидно, визначник AjB 6= 0.

Таким самими чином, як i для площини, можна показати, що мають мiсце такi властивостi визначникiв матриць переходу вiд одного базиса до iншого:

1±: Для довiльного базиса A справедлива рiвнiсть AjA = 1.

2±: Для довiльних трьох базисiв A, B, C викону¹ться рiвнiсть (AjB) ¢ (BjC) = AjC:

3±: Для довiльних двох базисiв A, B викону¹ться рiвнiсть (AjB) ¢ (BjA) = 1.

Нехай B ¹ множина всiх базисiв векторного простору V . Введемо на B бiнарне вiдношення ¢ однаково¨ орi¹нтацi¨ базисiв за допомогою наступного означення.

Означення 2.1. Будемо казати, що базиси A; B 2 B однаково орi¹нтованi (це познача¹ться як A¢B), ÿêùî AjB > 0.

Теорема 2.2. Вiдношення ¢ ¹ вiдношенням еквiвалентностi на множинi всiх базисiв B.

Доведення. Для довiльного базиса A 2 B за властивiстю 1± ìà¹ìî AjA = 1 > 0, òîìó A¢A. Îòæå, ¢ ¹ рефлексивне вiдношення.

Нехай для базисiв A; B 2 B ìà¹ìî A¢B, тобто AjB > 0, тому за властивiстю 3± íó¹òüñÿ íåðiâíiñòü BjA = > 0. Îòæå, B¢A. Таким чином, вiдношення ¢ симетричне.

Доведемо нарештi транзитивнiсть вiдношення ¢. Нехай базиси A; B; C 2 B задовольняють умови A¢B i B¢C, тобто AjB > 0 i BjC > 0. Згiдно властивостi 2± ìà¹ìî AjC = (AjB) ¢ (BjC) > 0, òîìó A¢C. Отже, транзитивнiсть доведена.

Нехай B=¢ ¹ фактор-множина2 множини всiх базисiв B по вiдношенню ¢. Доведемо,

що вона мiстить всього два елементи. Розглянемо базиси A = (~a1;~a2);~a3) i B = (~a2;~a1;~a3).

Îñêiëüêè ~a2 = 0~a1 + 1~a2 + 0~a3, ~a1 = 1~a1 + 0~a2 + 0~a3, ~a3 = 0~a1 + 0~a2 + 1~a3 òî

i KB класи еквiвалентностi вiдношення ¢, якi мiстять вiдповiдно базиси A i B. ßñíî, ùî

KA =6 KB, iнакше базиси A i B мали б однакову орi¹нтацiю. Розглянемо довiльний базис C 2 B. Згiдно властивостi 2± ìà¹ìî AjC = (AjB)(BjC) = (¡1)(BjC), тому визначники

AjC i BjC мають рiзнi знаки. Отже, або A¢C, або B¢C. Отже, або C 2 KA, àáî C 2 KB. Останн¹ означа¹, що B=¢ мiстить всього два елементи.

Означення 2.2. Кожний елемент фактор-множини B=¢ назива¹ться орi¹нтацi¹ю векторного простору V .

Один з елементiв множини B=¢ називають додатною орi¹нтацi¹ю, а iнший вiд'¹мною. В геометрi¨ на площинi розрiзняють два типи базисiв правий i лiвий. Якщо A =

називають правим базисом, якщо поворот навколо точки O вiд вектора ~a1 до вектора ~a2

викону¹ться проти руху годинниково¨ стрiлки, якщо дивитись на цi вектори з кiнця вектора ~a3, iнакше даний базис називають лiвим (дивись рисунок нижче на стор. 99). На практицi

2 тобто множина всiх класiв еквiвалентностi вiдношення ¢.

98

домовились за додатну орi¹нтацiю завжди вибирати правий базис. Простiр назива¹ться орi¹нтованим, якщо орi¹нтована множина всiх векторiв0 цього0 простору0 0 0 .

Два афiнних репери R = (O;~e1;~e2;~e3) i R = (O ;~e 1;~e 2;~e 3) кажуть, що вони однаково орi¹нтованi (протилежно орi¹нтованi), якщо базиси (~e1;~e2;~e3) i (~e 01;~e 02;~e 02) однаково

орi¹нтованi (протилежно орi¹нтованi). Зокрема, репер R = (O;~e1;~e2;~e3) називають додатно орi¹нтованим, якщо базис (~e1;~e2;~e3) належить додатнiй орi¹нтацi¨.

Для кращого вiзуального сприйняття афiнний репер R = (O;~e1;~e2;~e3) будемо називати

правим, коли направленi вiдрiзки OE1 2 ~e1, OE2 2 ~e2 i OE3 2 ~e3 розташованi як великий,

вказiвний i середнiй палець право¨ руки (якщо дивитись на розкриту долоню з кiнця середнього пальця), i будемо називати лiвим, коли ж цi направленi вiдрiзки розташованi вiдповiдно як великий, вказiвний i середнiй палець лiво¨ руки (якщо дивитись на розкриту долоню з кiнця середнього пальця). Як правило, орi¹нтацiю простору обирають так, щоб додатна орi¹нтацiя була правою. Отож, система координат викону¹ ще одне завдання, а саме, зада¹ орi¹нтацiю простору.

3 Перетворення афiнних координат в просторi

Постановка задачi. Вивiд формул перетворення афiнних координат в просторi. Паралельне перенесення початку координат та замiна координатних векторiв. Перетворення прямокутних координат в просторi. Ортогональнi матрицi.

Нехай у просторi задано двi афiннi системи координат (O;~e1;~e2;~e3) i (O0;~e 01;~e 02;~e 03).

99

Заради зручностi першу назвемо старою, а другу новою. Вiзьмемо точку M, i нехай ¨¨ координати у старiй системi (x; y; z), à ó íîâié (x0; y0; z0). Необхiдно старi координати x; y; z