
Prak_Geom1
.pdfДовiльне афiнне перетворення або зберiга¹ орi¹нтацiю простору, або змiню¹ його орi¹нтацiю. |
||||||
В першому випадку воно назива¹ться |
афiнним перетворенням першого роду, а в другому |
|||||
афiнним перетворенням другого роду. |
|
|
|
|
|
|
Можна показати, аналiтично афiннi перетворення простору визначаються такими |
||||||
формулами: |
x0 = c11x + c12y + c13z + x0; |
|
||||
|
(2.80) |
|||||
|
y0 = c21x + c22y + c23z + y0; |
|||||
|
z0 = c31x + c32y + c33z + z0; |
|
||||
де матриця |
0 c21 |
c22 |
c23 |
1; |
(2.81) |
|
|
||||||
|
|
c11 |
c12 |
c13 |
|
|
|
@ c31 |
c32 |
c33 |
A |
. |
|
складена з коефiцi¹нтiв при x; y; z, ¹ матриця переходу вiд репера R до репера R 0 |
|
|||||
Як i для випадку площини, можна довести, що множина всiх афiнних перетворень простору утворю¹ групу, яка назива¹ться групою афiнних перетворень простору. ˆ¨ пiдгрупами ¹ група подiбностей i група рухiв, а також всi ¨х пiдгрупи. Iншими прикладами пiдгруп афiнних перетворень ¹: а) множина всiх афiнних перетворень першого роду; б) множина всiх афiнних перетворень простору, кожне з яких залиша¹ фiксовану точку O
нерухомою; в) множина всiх афiнних перетворень простору, для кожного з яких визначник матрицi (2.81) дорiвню¹ одиницi (група еквiафiнних перетворень простору).
Тепер можна дати загальне означення геометрi¨. Геометрiя це наука, яка вивча¹ такi властивостi фiгур, якi залишаються iнварiантними при всiх перетвореннях деяко¨ групи.
131
2.4Вивчення поверхонь другого порядку за канонiчними рiвняннями
1 Поверхнi другого порядку. Метод перерiзiв
Рiвняння поверхнi в просторi. Алгебра¨чна поверхня та ¨¨ порядок. Поверхня другого порядку та ¨¨ загальне рiвняння. Дослiдження поверхонь методом перерiзiв.
При аналiтичному пiдходi будь-яка геометрична фiгура у просторi з обраною системою |
|
координат зада¹ться рiвнянням або нерiвнiстю (або ¨х системою), яке (якi) задовольняють |
|
координати кожно¨ точки, що належить фiгурi, i не задовольняють координати жодно¨ точки, |
|
якi не належать цiй фiгурi, зокрема рiвняння |
|
F (x; y; z) = 0 |
(2.82) |
зада¹ у просторi поверхню.
Всi поверхнi дiляться на два великих класи: алгебра¨чнi та неалгебра¨чнi (або трансцендентнi). Поверхня S назива¹ться алгебра¨чною, якщо в деякiй афiннiй системi
координат ¨¨ рiвняння можна записати у виглядi (2.82), в якому F (x; y; z) многочлен вiдносно x; y; z, тобто алгебра¨чна сума скiнченно¨ множини членiв виду
êîåôiöi¹íò a дiйсне число, вiдмiнне вiд нуля, а p; q i r невiд'¹мнi цiлi числа. Число p + q + r назива¹ться степенем члену axpyqzr, äå a =6 0. Степенем многочлена назива¹ться
найвищий iз степеней його членiв. Порядком алгебра¨чно¨ поверхнi називають степiнь ¨¨ рiвняння в якiй-небудь афiннiй системi координат (тобто степiнь многочлена F (x; y; z) â
рiвняннi (2.82) цi¹¨ поверхнi).
В даному роздiлi ми будемо вивчати поверхнi другого порядку.
Означення 2.6. Множина точок простору, координати яких задовольняють рiвняння
a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0; (2.83)
äå a11; a22; : : : ; a44 дiйснi числа, причому хоча би один iз коефiцi¹нтiв a11; a22; a33 íå дорiвню¹ нулю, назива¹ться поверхнею другого порядку.
Рiвняння (2.83) згодом ми будемо називати загальним рiвнянням поверхнi другого порядку.
Основним методом вивчення форми поверхонь буде метод перерiзiв, сутнiсть якого у тому, що поверхню S перетинають площинами, паралельними координатним площинам, i
визначають лiнi¨ перетину поверхнi з даними площинами. За виглядом цих лiнiй роблять висновок про форму дано¨ поверхнi. В основi цього методу лежить така теорема.
Теорема 2.13. Якщо поверхня |
|
у прямокутнiй декартовiй системi координат |
|
~~ ~ |
||||||
зада¹ться рiвнянням |
S |
|
|
|
|
|
|
|
Oi j k |
|
|
|
F (x; y; z) = 0; |
|
|
|
|
(2.84) |
|||
|
|
|
|
|
|
|
||||
то проекцiя лiнi¨ перетину поверхнi |
|
з площиною |
|
на площину |
|
у системi |
~~ |
|||
ма¹ рiвняння |
|
|
S |
|
z = h |
|
Oxy |
|
|
Oi j |
|
|
|
F (x; y; h) = 0: |
|
|
|
|
(2.85) |
||
|
|
|
|
|
|
|
|
|||
132
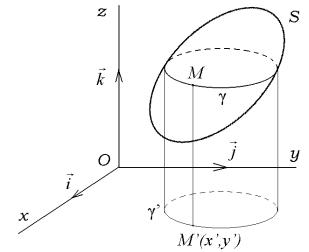
Доведення. Нехай ° лiнiя перетину поверхнi S i площини z = h, à °0 ¨¨ проекцiя на площину Oxy (див. рисунок).
Вiзьмемо довiльну |
точку |
M0 ëiíi¨ °0, |
||
яка у системi |
~~ |
íà |
площинi |
|
|
Oi j |
|
|
Oxy |
ма¹ координати (x0; y0). Тодi у системi
~~ ~
координат Oi j k вона ма¹ координати (x0; y0; 0), а оскiльки точка M0 належить °0, то вона ¹ проекцi¹ю дано¨ точки M криво¨ °, причому ця точка ма¹ координати
(x0; y0; h) i належить поверхнi |
S. Òîìó |
¨¨ координати задовольняють |
рiвняння |
(2.84), тобто F (x0; y0; h) = 0. Таким чином,
показано, що координати кожно¨ точки M0, що належить лiнi¨ °0, задовольня¹ рiвняння (2.85). Вiзьмемо на площинi Oxy будь-яку точку M¤(x¤; y¤), яка не належить лiнi¨ °0. Проведемо через точку M¤ пряму, паралельну осi Oz i позначимо через M точку перетину
цi¹¨ прямо¨ з площиною |
|
. Тодi у системi координат |
~~ ~ |
точка |
|
ма¹ координати |
|
z = h |
Oi j k |
|
M |
|
|
(x¤; y¤; h), à îñêiëüêè M¤ |
не належить °0, то точка M |
не належить |
êðèâié °, à îòæå, |
|||
i поверхнi S. Таким чином, координати точки M не задовольняють рiвняння (2.85),
тобто F (x¤; y¤; h) = 0. Отож, справдi, координати кожно¨ точки, яка належить |
ëiíi¨ |
|
6 |
°0 |
, íå |
°0, задовольняють рiвняння (2.84), а координати жодно¨ точки, яка не належить |
|
|
задовольняють його, тобто рiвняння (2.85) ¹ рiвнянням проекцi¨ лiнi¨ перетину поверхнi S з площиною z = h. ¤
Зауваження. Аналогiчнi теореми можна довести для випадку, коли поверхню S перетинатимемо площинами, паралельними координатним площинам Oxz i Oyz.
Íàñëiäîê 2.3. Ëiíiÿ ° перетину поверхнi S з площиною ¾, паралельнiй площинi Oxy, рiвна проекцi¨ °0 цi¹¨ лiнi¨ на площину Oxy.
~
Доведення. Дiйсно, паралельне перенесення на вектор p~ = ¡hk переводить кожну точку M 2 ° у вiдповiдну точку M0 2 °0. Îòæå, iñíó¹ ðóõ, ÿêèé ñóìiù๠ëiíiþ ° ç ëiíi¹þ °0, à öå означа¹, що цi лiнi¨ рiвнi. 
2 Поверхнi обертання
Означення поверхнi обертання. Знаходження рiвняння поверхнi обертання навколо координатно¨ осi.
Розглянемо тепер так званi поверхнi обертання, тобто поверхнi, якi отримуються в результатi обертання тих чи iнших лiнiй навколо прямих.
Означення 2.7. Поверхню, яка разом з кожною сво¹ю точкою мiстить все коло, утворене обертанням цi¹¨ точки навколо фiксовано¨ прямо¨ l, назива¹ться поверхнею обертання, а
пряму l, навколо яко¨ здiйсню¹ться обертання, називають вiссю обертання.
Наголосимо, що обертання кожно¨ точки поверхнi навколо осi l вiдбува¹ться у площинi,
перпендикулярнiй осi l. Тодi очевидно, що у перерiзi поверхнi обертання площинами, перпендикулярними до осi обертання, дiста¹мо кола, якi називають паралелями. Кривi, якi
133
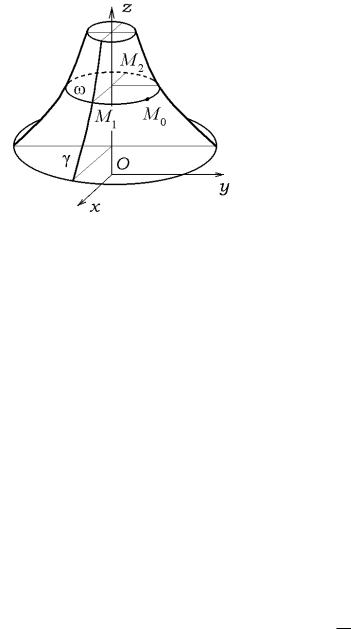
¹ лiнiями перетину поверхнi обертання пiвплощинами, що визначаються вiссю обертання l,
називають меридiанами. На цiй пiдставi ста¹ очевидним той факт, що поверхня обертання може бути отримана обертанням плоско¨ криво¨ ° (вона породжу¹ сiм'ю меридiанiв) навколо
прямо¨ l, яка з кривою ° лежить в однiй площинi, причому, як свiдчить наступна теорема, ¨¨ аналiтичне задання (рiвняння) можна знайти за рiвнянням криво¨ °.
Теорема 2.14. Якщо у прямокутнiй декартовiй системi координат Oxyz криву ° ó
площинi Oxz задано рiвнянням |
|
|
|
x = f(z); |
(2.86) |
то рiвняння |
x2 + y2 = f2(z) |
(2.87) |
|
¹ рiвнянням поверхнi, утворено¨ обертанням криво¨ ° навколо осi Oz.
Доведення. Нехай S поверхня, утворена обертанням криво¨ x = f(z), навколо осi Oz, i
нехай M0(x0; y0; z0) 2 S. Якщо через точку M0 провести площину, перпендикулярну |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
äî îñi Oz, то згiдно з означенням вона перетина¹ |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
поверхню S |
ïî |
êîëó |
!, центром |
якого |
¹ |
|
|
точка |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
M0(0; 0; z0), ïðè÷îìó öå коло перетина¹ площинó xOz |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
M2(¡ |
p |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
у точках M1( |
x02 + y02; 0; z0), |
|
x02 + y02; 0; z0). |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Îñêiëüêè êîëî ! паралель поверхнi S, утворено¨ |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
обертанням криво¨ x = f(z) навколо осi Oz, òî àáî |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
точка M1, àáо точка M2 |
належèòü êðèâié °, à îòæå, |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
àáî |
p |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x02 + y02 = f(z0), àáî ¡ |
x02 + y02 = f(z0). ßêùî |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
обидвi частини вiдповiдного рiвняння пiднести до |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
квадрату, то отрима¹мо: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x02 + y02 = f2(z0); |
|
|
|
|
|
|
|
|
|
|
||||
тобто координати (x0; y0; z0) точки M0 задовольняють рiвняння (2.87). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Нехай точка M0(x0; y0; z0) не належить поверхнi S. Тодi жодна з точок M1( |
|
x02 + y02; 0; z0), |
|||||||||||||||||||||||||
|
|
|
|
p |
|
|
|
|
|
M0 íå |
|
p |
|
|
|
|
), i |
p |
|
|
|
|
|
|
|
|
|
|
|
M |
2 |
( |
|
|
x2 |
+ |
y2 |
; ; z |
0) |
не належить кривiй °, тобто i |
x2 |
+ y2 |
= f(z |
|
x2 |
+ y2 |
= |
f |
( |
z |
0) |
. À |
|||||||
|
¡ |
0 |
0 |
0 |
|
|
|
|
0 |
0 |
6 |
0 |
|
¡ |
0p |
0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|||
це й означа¹, що координати точки |
|
задовольняють рiвняння (2.87). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Таким |
чином, |
показано, що координати кожно¨ |
точки, |
яка належить |
поверхнi |
S, |
|||||||||||||||||||||
задовольня¹ рiвняння (2.87), а координати жодно¨ точки, яка не належить поверхнi S,
не задовольня¹ рiвняння (2.87), тобто рiвняння (2.87) ¹ рiвнянням поверхнi, утворено¨ обертанням криво¨ x = f(z) навколо осi Oz. 
Зауваження. Аналогiчно можна переконатись в тому, що в прямокутнiй системi координат рiвняння z2 + y2 = g2(x) визнача¹ поверхню обертання, утворену обертанням
навколо осi Ox лiнi¨, задано¨ рiвнянням y = g(x) в площинi Oxy, а рiвняння x2 + z2 = h2(y) визнача¹ поверхню, утворену обертанням навколо осi Oy лiнi¨, задано¨ рiвнянням x = h(y) â
площинi Oxy.
Приклад 1. Написати рiвняння поверхнi, утворено¨ обертанням параболи
z2 ¡ 2px = 0; y = 0;
äå p > 0, навколо осi Oz.
Розв'язання. Рiвняння поверхнi, утворено¨ обертанням криво¨
x= z2 ;
2p
134

що знаходиться в площинi Oxz, згiдно з теоремою 2.14 матиме вигляд
x2 + y2 |
= |
z4 |
|
|
4p2 |
|
|||
|
|
|
||
àáî z4 = 4p2(x2 + y2), яка ¹ поверхнею обертання четвертого порядку. |
¤ |
|||
Приклад 2. В площинi Oxz прямокутно¨ системи координат Oxyz äàíî êîëî x2+z2 = r2 ç центром в початку координат радiуса r. Написати рiвняння поверхнi S, утворено¨ обертанням цього кола навколо осi Oz.
Розв'язання. Спочатку запишемо рiвняння виду (2.86) лiнi¨ °, вiд обертання яко¨ навколо осi Oz утворю¹ться поверхня. З рiвняння даного кола знаходимо: x = §pr2 ¡ z2, äå
кожен знак перед коренем визнача¹ певне напiвколо даного кола.
Ясно, що при обертаннi навколо осi Oz кожного з цих напiвкiл отриму¹ться та ж сама
поверхня, що i при обертаннi всього кола, тому за лiнiю ° вiзьмемо, наприклад, напiвколо, яке у площинi Oxz визнача¹ться рiвнянням x = pr2 ¡ z2.
За доведеною теоремою 2.14 рiвняння поверхнi S ì๠âèä:
|
2 |
|
2 |
|
p |
|
|
|
|
2 |
x |
+ y |
= ( |
r |
2 |
2 |
) |
||||
|
|
|
|
¡ z |
|
àáî x2 + y2 + z2 |
= r2. Таким чином, поверхня S ¹ сфера радiуса r з центром в початку |
координат. |
¤ |
3 Цилiндричнi та конiчнi поверхнi другого порядку
Означення цилiндрично¨ та конiчно¨ поверхнi Цилiндричнi та конiчнi поверхнi другого порядку, ¨х канонiчнi рiвняння. Цилiндричнi та конiчнi перерiзи.
Якщо у просторi обрано систему координат, то поверхня зада¹ться рiвнянням
F (x; y; z) = 0; (2.88)
тобто поверхнею ¹ множина всiх тих точок простору, координати яких задовольняють рiвняння (2.88). Очевидно, що найпростiшою поверхнею ¹ площина, рiвняння яко¨ ¹ лiнiйне рiвняння
Ax + By + Cz + D = 0;
äå A2 + B2 + C2 6= 0, а от наступною за нею в порядку простоти ¹ цилiндрична поверхня.
Означення 2.8. Поверхня, яка ма¹ ту властивiсть, що разом з кожною сво¹ю точкою вона мiстить всю пряму, яка проходить через цю точку паралельно даному ненулевому вектору p~, назива¹ться цилiндричною поверхнею, або цилiндром.
Прямi, якi паралельнi вектору p~ i лежать на цилiндричнiй поверхнi, називаються
твiрними цi¹¨ поверхнi. Очевидно, що цилiндричну поверхню можна утворити так. Якщо ° деяка лiнiя, а p~ ненулевий вектор, то поверхня, утворена прямими, якi проходять
через всi точки лiнi¨ ° i паралельнi вектору p~, буде цилiндричною. У цьому разi лiнiю °
називають напрямною цi¹¨ поверхнi.
З допомогою прямих можна утворити ще одну поверхню.
Означення 2.9. Конiчною поверхнею або конусом з вершиною у точцi M0 називають поверхню, яка ма¹ властивiсть, що разом з кожною сво¹ю точкою M, ùî íå çáiãà¹òüñÿ ç
точкою M0, ця поверхня мiстить i пряму M0M.
135
Точку M0 називають вершиною, а прямi, якi проходять через цю точку i лежать на поверхнi, ¨¨ твiрними. Очевидно, що конiчну поверхню можна утворити так. Якщо M0 точка простору, а ° деяка лiнiя, що не проходить через точку M0, то поверхня, утворена усiма прямими, кожна з яких проходить через M0 i деяку точку лiнi¨ °, áóäå êîíi÷íîþ.
З'ясу¹мо, як аналiтично описуються цилiндричнi та конiчнi поверхнi, тобто складемо ¨х |
||||||
рiвняння. Це буде зроблено за умови, що у просторi обрана прямокутна декартова система |
||||||
координат, плоска крива ° задана системою рiвнянь |
|
|||||
( |
f |
( |
x; y) |
= |
0; |
|
|
z |
= |
h; |
(2.89) |
||
твiрнi цилiндрично¨ поверхнi паралельнi осi Oz, вершина конiчно¨ поверхнi точка M0 íå належить площинi z = h.
Теорема 2.15. |
Рiвняння |
f(x; y) = 0 |
(2.90) |
|
|
¹ рiвнянням цилiндрично¨ поверхнi S, напрямною яко¨ ¹ лiнiя °, а твiрними прямi, паралельнi осi Oz.
Доведення. Нехай M0(x0; y0; z0) довiльна фiксована точка простору, i нехай M0 належить площинi z = h. Òîäi, ÿêùî M0 належить поверхнi S, то вона належить лiнi¨ °, а отже, координати (x0; y0; h) точки M0 задовольняють рiвняння (2.90). Якщо ж M0 не належить поверхнi S, то вона не належить лiнi¨ °, а отже, координати (x0; y0; h) точки M0 íå задовольняють рiвняння (2.90). Нехай точка M0 не належить площинi z = h. Тодi пряма,
паралельна осi Oz, перетина¹ площину z = h ó òî÷öi M1(x0; y0; h), яка на площинi z = h
~~
у системi координат Oi i ма¹ координати (x0; y0). Якщо точка M0 належить поверхнi S, то пряма M0M1 ¹ твiрною, тому точка M1 належить лiнi¨ °. Тодi координати (x0; y0; h) точки M1 задовольняють рiвняння (2.89), тобто f(x0; y0) = 0. А це, у свою чергу, означа¹, що
координати (x0; y0; z0) точки M0 задовольняють рiвняння (2.90).
Нехай точка M0 не належить поверхнi S. Òîäi M1 не належить лiнi¨ °, i ¨¨ координати (x0; y0; h) не задовольняють (2.89), тобто f(x0; y0) 6= 0. А це означа¹, що координати (x0; y0; z0) точки M0 не задовольняють рiвняння (2.90). Таким чином, показано, що координати кожно¨ точки, яка належить поверхнi S, задовольня¹ рiвняння (2.90), а координати жодно¨ точки,
яка не належить поверхнi S, не задовольняють рiвняння (2.90), тобто рiвняння (2.90) ¹ рiвнянням цилiндрично¨ поверхнi, напрямною яко¨ ¹ лiнiя °, а твiрними прямi, паралельнi осi Oz. 
Якщо (2.89) ¹ кривою другого порядку, то вiдповiдну цилiндричну поверхню називають |
||||||
цилiндричною поверхнею другого порядку, а ¨х рiвняння мають вигляд: |
||||||
|
x2 |
+ |
y2 |
|
= 1 елiптичний цилiндр; |
|
|
a2 |
|
b2 |
|
||
|
|
|
|
|
||
|
x2 |
¡ |
y2 |
|
= 1 гiперболiчний цилiндр; |
|
|
a2 |
b2 |
|
|||
y2 = 2px параболiчний цилiндр;
136
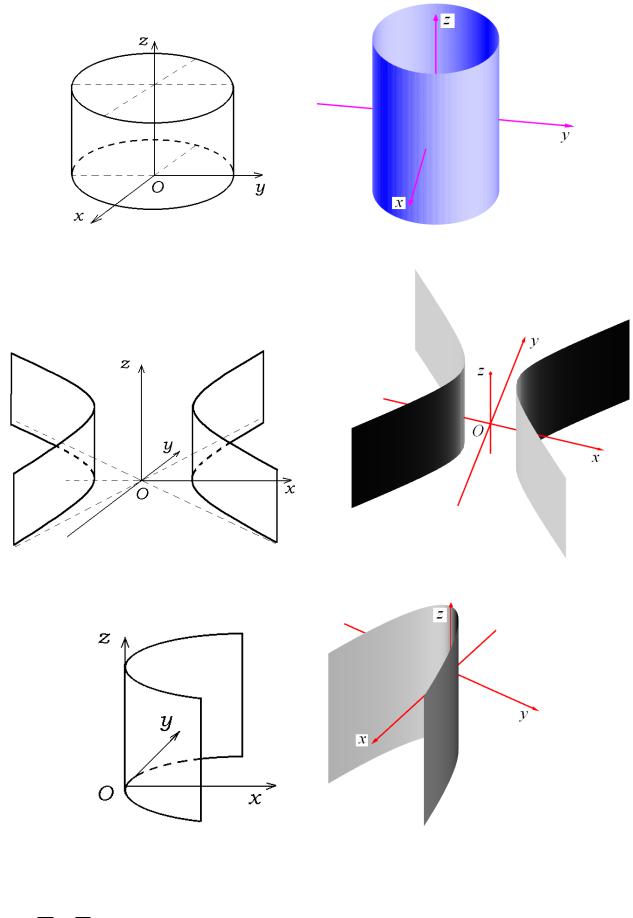
Елiптичний цилiндр.
Гiперболiчний цилiндр.
Параболiчний цилiндр.
x2 ¡ y2 = 0 цилiндр, який розпався на пару площин, що перетинаються;
a2 b2
137

x2 ¡ a2 = 0 цилiндр, який розпався на пару паралельних площин;
x2 = 0 цилiндр, який явля¹ собою пару площин, що збiгаються (площина Oyz).
Нехай ма¹мо лiнiю °, задану системою рiвнянь (2.89), i нехай точка M0(x0; y0; z0) не належить цiй площинi.
Теорема 2.16. Рiвняння |
(x ¡ x0) + x0 |
; z ¡¡ z0 |
(y ¡ y0) + y0 |
¶ |
= 0 |
(2.91) |
||
f |
µz ¡¡ z0 |
|||||||
|
|
h z0 |
|
h z0 |
|
|
|
|
¹ рiвнянням конiчно¨ поверхнi S, напрямною яко¨ ¹ лiнiя °, а точка M0 ¨¨ вершиною. Доведення. Нехай M¤(x¤; y¤; h) довiльна, але фiксована точка лiнi¨ °. Тодi рiвняння
x ¡ x0 |
= |
y ¡ y0 |
= |
z ¡ z0 |
|
|
z¤ ¡ z0 |
||
x¤ ¡ x0 |
y¤ ¡ y0 |
|||
¹ рiвняння прямо¨, що проходить через точки M0 M¤ у площинi z = a подаються у виглядi
x¤ = h ¡ z0 (x ¡ x0) + x0; y¤ = z ¡ z0
i M¤. А отже, координати
h ¡ z0 (y ¡ y0) + y0: z ¡ z0
(x¤; y¤) точки
(2.92)
Пiдставивши ¨х у рiвняння f(x; y) = 0, дiстанемо (2.91).
Якщо точка M(x; y; z) належить поверхнi S (M 6= M0), то вона лежить на прямiй, що проходить через точку M0 i деяку точку M¤ íà ëiíi¨ °, координати яко¨ визначаються за
формулами (2.92). А отже, вони задовольняють рiвняння (2.91). Якщо ж точка M(x; y; z) íå
належить поверхнi S, то прямiй, що проходить через точки M0 i M, не належить жодно¨ точки лiнi¨ °, тобто нiяка пара (x¤; y¤), визначена за формулами (2.90), не задовольня¹ рiвняння
f(x; y) = 0. А це означа¹, що координати точки M не задовольняють рiвняння (2.91). Теорема доведена. 

Приклад 1. Скласти рiвняння поверхнi S, утворено¨ прямими, якi проходять через точку
M0(0; 0; h) i дотикаються кулi радiуса r з центром у початку координат (h > r).
Розв'язання. Згiдно з умовою такi прямi утворюють конiчну поверхню, вершиною яко¨ ¹ точка M0(0; 0; h), а напрямною коло, задане системою рiвнянь
8 x2 + y2 = r2 ¡ h2 ; |
|||||
> |
|
r2 |
|
r4 |
|
> |
|
|
|
|
|
< |
z = |
|
: |
|
|
h |
|
|
|||
> |
|
|
|
|
|
> |
|
|
|
|
|
: |
|
|
|
|
|
Тому за теоремою 2.16 рiвняння цi¹¨ поверхнi запису¹ться у виглядi
0 h ¡ h x1 |
|
+ 0 h ¡ h y1 |
= r2 r |
2 |
|||||||
|
|
r2 |
|
2 |
|
r2 |
|
2 |
|
|
|
B z ¡ h |
C |
|
B z ¡ h |
C |
|
|
|
4 |
|||
|
|
¡ h |
|
||||||||
@ |
|
|
A |
|
@ |
|
A |
|
|
|
|
àáî |
|
r2 |
|
|
|
|
¤ |
||
x2 + y2 |
= |
|
(z ¡ h)2: |
|
h2 ¡ r2 |
||||
138

Будемо вважати, що вершиною конiчно¨ поверхнi ¹ початок координат, а напрямною
лiнi¹ю ¹ крива (
a11x2 + 2a12xy + a22y2 + 2a10x + 2a20y + a00 = 0;
z = h:
Тодi за теоремою 2.16 рiвняння вiдповiдно¨ конiчно¨ поверхнi другого порядку запису¹ться у |
||||||||
виглядi |
|
a20 |
|
a00 |
|
|
|
|
a11x2 + 2a12xy + a22y2 + 2 |
a10 |
xz + 2 |
yz + |
z2 |
= 0: |
(2.93) |
||
h |
h |
|
||||||
|
|
|
h2 |
|
|
|||
Отож ма¹мо ознаку, за якою зможемо розрiзняти конiчнi поверхнi другого порядку, а саме: його лiва частина ¹ однорiдним многочленом другого степеня вiдносно x; y; z.
Зокрема, якщо напрямна ° конiчно¨ поверхнi S задана однi¹ю з систем рiвнянь:
à)
â)
8 a2 |
+ b2 = 1; |
||||
|
x2 |
y2 |
|||
: |
|
|
|
|
|
|
|
z = h; |
|||
< |
|
|
|||
( |
y2 = 2px; |
||||
|
z = h; |
||||
á)
ã)
8< x2 ¡ y2 = 1; : a2 b2
z = h;
8< x2 ¡ y2 = 0; : a2 b2
z = h
i вершина збiга¹ться з початком координат, то рiвняння конiчно¨ поверхнi S ма¹ вiдповiдно вигляд:
à') |
x2 |
|
y2 |
z2 |
|
á') |
x2 |
y2 |
z2 |
|||||||||||
|
+ |
|
|
|
¡ |
|
= 0; |
|
|
|
|
¡ |
|
|
¡ |
|
= 0; |
|||
a2 |
b2 |
c2 |
|
a2 |
b2 |
c2 |
||||||||||||||
â') y2 |
¡ 2 |
p |
|
|
|
ã') |
x2 |
¡ |
y2 |
|
|
|
|
|
|
|||||
|
xz = 0; |
|
|
= 0: |
|
|
|
|||||||||||||
c |
a2 |
b2 |
|
|
|
|||||||||||||||
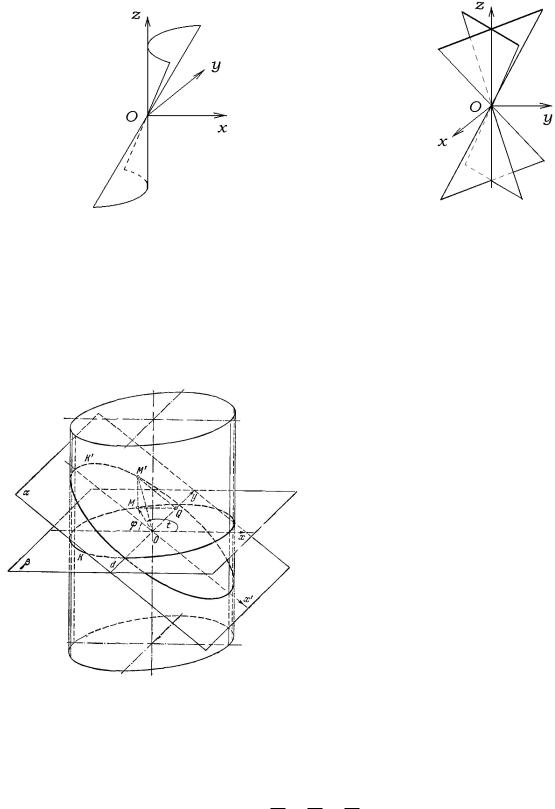
а') Елiптичний конус. б') Гiперболiчний конус.
Проведемо дослiдження лiнiй перетину цилiндричних поверхонь з рiзними площинами. Нехай ма¹мо елiптичний цилiндр, заданий рiвнянням
x2 + y2 = 1; a2 b2
i площину ¼, задану рiвнянням
Ax + By + Cz + D = 0:
139
Якщо площина ¼ паралельна осi Oz, то вона перетина¹ площину Oxy ïî ïðÿìié Ax + By + D = 0. А пряма може або перетинати елiпс у двох точках, або дотикаються
його, або не перетинатися з ним. У зв'язку з цим площина ¼, паралельна осi Oz, ìîæå
перетинати елiптичний цилiндр або по двох твiрних (лiнiя перетину двi паралельнi прямi), або дотикатись цилiндра вздовж твiрно¨ (лiнiя перетину одна пряма).
в') Параболiчний конус. |
г') Конус, напрямна якого двi прямi, що |
|
перетинаються. |
||
|
Якщо ж площина ¼ не паралельна осi Oz (C =6 0), то, обравши у нiй систему координат
(O0;~e1;~e2), äå |
µ0; 0; C ¶ |
; ~e1 |
=~i ¡ C~k; ~e2 |
= ~j ¡ C |
~k; |
|
|
|
|
|||||||||||
O0 |
|
|
|
|
||||||||||||||||
|
|
D |
|
|
|
A |
|
|
|
|
|
B |
|
|
|
|
|
|||
ма¹мо, що точка M(x; y; z) перетину елiптичного цилiндра з площиною ¼, тобто точка, |
||||||||||||||||||||
|
|
|
|
|
координати яко¨ задовольняють умови |
|
||||||||||||||
|
|
|
|
|
|
|
x2 |
y2 |
|
|
|
Ax + By + D |
|
|||||||
|
|
|
|
|
|
|
|
|
+ |
|
= 1; z = ¡ |
|
|
; |
||||||
|
|
|
|
|
|
|
|
a2 |
b2 |
|
C |
|||||||||
|
|
|
|
|
ма¹ координати x0 |
= x; y0 |
= y. Тодi рiвняння |
|||||||||||||
|
|
|
|
|
лiнi¨ перетину ма¹ вигляд |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(x0)2 |
(y0)2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
= 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
|
|||
тобто ¹ лiнi¹ю другого порядку. А оскiльки ця лiнiя обмежена, то вона ¹ елiпсом. Таким чином, будь-який перерiз елiптичного цилiндра площиною, не паралельною твiрним, ¹ елiпс. В такий же саме спосiб можна переконатись, що лiнi¹ю перетину гiперболiчного (параболiчного) цилiндра з площиною ¹ або двi паралельнi пря-
мi, або одна пряма, якщо площина паралельна осi Oz, або гiпербола (парабола), якщо площина не паралельна осi Oz.
Проведемо дослiдження лiнiй перетину конiчних поверхонь з рiзними площинами, причому вiзьмемо елiптичний конус, заданий рiвнянням
x2 + y2 ¡ z2 = 0; a2 b2 c2
140
