
Беркетов_ответы_на_билеты
.pdf
1. Системы: основные понятия и определения.
Система – целенаправленная совокупность взаимодействующих элементов, объединённых единой целью. В результате образования системы возникает системный (синергетический) эффект.
При рассмотрении систем управления к свойствам системы добавляют свойства самоорганизации (развития) и способность к выработке целей.
Системный подход – изучаемые объекты рассматриваются как система.
Основной парадигмой в современной науке является системный подход. Т.е. в ходе его изучения он разбивается на части (элементы) и описывается взаимодействие этих элементов.
Классический системный подход получил дальнейшее развитие, при котором изучаемая система рассматривается как подсистема более общей системы. Кроме того, рассматриваются взаимодействия системы с внешней средой.
Системный подход — это элемент учения об общих законах развития природы и одно из выражений диалектического учения. Можно привести разные определения системного подхода, но наиболее правильно то, которое позволяет оценить познавательную сущность этого подхода при таком методе исследования систем, как моделирование. Поэтому весьма важны выделение самой системы S и внешней среды Е из объективно существующей реальности и описание системы исходя из общесистемных позиций.
При системном подходе к моделированию систем необходимо прежде всего четко определить цель моделирования. Поскольку невозможно полностью смоделировать реально функционирующую систему (системуоригинал, или первую систему), создается модель (система-модель, или вторая система) под поставленную проблему.
2. Понятие модели. Классификация систем и моделей.
Современная научная парадигма предполагает изучение объектов посредством их моделирования. Моделирование – замена исходной системы другой системой (аналогом), в которой отражаются основные
(существенные) свойства моделируемой системы.
Отнесение свойства к множеству существенных является в определённой мере условным и зависит от цели исследования.
Модель, адекватная системе – модель, которая правильно отражает изучаемые свойства системы.
Классификация моделей
•Физические модели (аналоговые)
Макеты (макет дома, самолёта…), тренажёры.
•Символьные модели (знаковые)
Символьные модели могут иметь различную природу, в зависимости от своего предназначения. Географические карты (графические модели местности), чертежи.
Знаковые модели, использующие специальные модели знаков (символов)
Математические модели
При описании знаковых моделей используются специальные языки. В принципе, объект может быть описана на естественном языке – семантическая модель.
Математические модели описываются на языке математики, т.е. они представляют некоторые математические объекты (уравнение, теория случайных процессов, формулы мат. логики и тп).
Математическая модель понимается как абстрактная система.
В зависимости от различных признаков (критериев) системы и модели относятся к тем или иным классам (проводится их классификация).
Классификация систем
Статические системы
Фактор времени не играет важной роли и поэтому не учитывается.
Динамические системы
Время играет существенную роль, потому фактор времени учитывается – система функционирует во времени.
При описании динамических систем используется понятие состояние системы.
Состояние системы – т.е. системы описываются набором переменных состояний (z1 , z2 , …, zk ). Математически состояние системы можно интерпретировать в виде точки k-мерного пространства – фазовое
пространство. Движение (функционирование) системы можно иллюстрировать в виде некоторой кривой (траекторией движения/функционирования системы).
В динамической системе связь входных и выходных параметров можно представить в виде: Y = F (X, Z, t) X = (x1, x2, …, xn) Z = (z1, z2, … , zk) Y = (y1, y2, …, ym)
где X – вектор входных параметров, Z – вектор состояний, Y – вектор выходных состояний, F – вектор функции, t - время.
Непрерывные системы
Состояние непрерывных систем меняется постоянно с течением времени.
Дискретные системы
Изменение состояний происходит в отдельные (выделенные) моменты времени.

Например, модель парикмахерской можно отнести к дискретным системам. Изменения состояния происходит в моменты прихода клиентов, а также загрузки или высвобождения парикмахера.
Аналитическая модель – такая математическая модель, которая представлена аналитическими математическими объектами (дифф. уравнения или их системы, интегральные уравнения и тд).
Исследование таких моделей сводится к решению соответствующих уравнений или систем уравнений. Решения стремятся произвести аналитическими методами.
Иногда аналитическое решение не удаётся, тогда используются численные методы. Это означает, что модель (система) дискретизируется, т.е. непрерывная система заменяется дискретной.
Детерминированные модели (системы)
Поведение детерминированных систем полностью определяется набором начальных параметров.
Стохастические модели (системы)
Подвержены случайным факторам. Поведение (функционирование) стохастических систем
подвержено случайным флуктуациям (отклонениям, нарушениям).
Дискретно-событийная система (модель) – такая динамическая система (модель), в которой изменение её состояний происходит под воздействием потока событий.
Событие – наступление определённого комплекса условий.
Например, состояние модели парикмахерской меняется только в моменты прихода клиентов, начала или окончания обслуживания клиента парикмахера (это и есть события).
3. Принципы системного подхода в моделировании систем.
При построении моделей объектов используется системный подход, представляющий собой методологию решения сложных задач, в основе которой лежит рассмотрение объекта как системы, функционирующей в некоторой среде.
Системный подход предполагает раскрытие целостности объекта, выявление и изучение его внутренней структуры, а также связей с внешней средой. При этом объект представляется как часть реального мира, которая выделяется и исследуется в связи с решаемой задачей построения модели.
Кроме этого, системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит цель проектирования, а объект рассматривается во взаимосвязи с окружающей средой .
Сложный объект может быть разделен на подсистемы, представляющие собой части объекта, удовлетворяющие следующим требованиям:
1)подсистема является функционально независимой частью объекта. Она связана с другими подсистемами, обменивается с ними информацией и энергией;
2)для каждой подсистемы могут быть определены функции или свойства, не совпадающие со свойствами всей системы;
3)каждая из подсистем может быть подвергнута дальнейшему делению до уровня элементов.
Вданном случае под элементом понимается подсистема нижнего уровня, дальнейшее деление которой нецелесообразно с позиций решаемой задачи.
Независимо от типа модели при ее построении необходимо руководствоваться рядом принципов системного подхода:
1)последовательное продвижение по этапам создания модели;
2)согласование информационных, ресурсных, надежностных и других характеристик;
3)правильное соотношение различных уровней построения модели;
4)целостность отдельных стадий проектирования модели.
4. Имитационное моделирование. Метод статистического моделирования.
Имитационное моделирование (в широком смысле) - есть процесс конструирования модели реальной системы и постановки экспериментов на этой модели с целью либо понять поведение системы, либо оценить (в рамках накладываемых ограничений) различные стратегии, обеспечивающие функционирование данной системы.
Имитационное моделирование (в узком смысле) - это представление динамического поведения системы посредством продвижения ее от одного состояния к другому в соответствии с хорошо известными операционными правилами (алгоритмами).
Итак, для создания имитационной модели надо выделить и описать состояния системы и алгоритмы (правила) его изменения. Далее это записывается в терминах некоторого инструментального средства моделирования (алгоритмического зыка, специализированного языка) и обрабатывается на ЭВМ.
Имитационная модель- это логико-математическое описание системы, которое может быть использовано в ходе проведения экспериментов на цифровой ЭВМ.
Под имитацией будем понимать численный метод проведения на ЭВМ экспериментов с математическими моделями, описывающими поведение сложных систем в течение продолжительного времени.
Что позволяет имитационное моделирование:
С ИМ проводятся машинные эксперименты, которые позволяют сделать выводы о поведении системы:

•без ее построения, если это проектируемая система;
•без вмешательства в ее функционирование, если это действующая система, экспериментирование
скоторой невозможно или нежелательно (дорого, опасно);
•без ее разрушения, если цель эксперимента состоит в определении предельного воздействия на
систему.
На этапе исследования и проектирования систем при построении и реализации машинных моделей (аналитических и имитационных) широко используется метод статистических испытаний (Монте-Карло), который базируется на использовании случайных чисел, т. е. возможных значений некоторой случайной величины с заданным распределением вероятностей.
Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистических данных о процессах, происходящих в моделируемой системе.
Для получения представляющих интерес оценок характеристик моделируемой системы S с учетом воздействий внешней среды Е статистические данные обрабатываются и классифицируются с использованием методов математической статистики
Таким образом, сущность метода статистического моделирования сводится к построению для процесса функционирования исследуемой системы S некоторого моделирующего алгоритма, имитирующего поведение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды Е, и реализации этого алгоритма с использованием программно-технических средств ЭВМ.
5. Основные подходы к построению математических моделей систем.
Под математической моделью объекта (реальной системы) понимают конечное подмножество переменных {х (t),v (t), h (/)} вместе с математическими связями между ними и характеристиками у.
совокупность входных воздействий на систему xi Є X, i=1, Nxi
совокупность воздействий внешней среды vl Є V, l=1, Nv
совокупность внутренних (собственных) параметров системы hk ЄH, k= 1, nh
совокупность выходных характеристик системы
При построении математических моделей процессов функционирования систем можно выделить следующие основные подходы:
непрерывно-детерминированный (например, дифференциальные уравнения);
Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной или нескольких переменных, причем в уравнение входят не только функции, но и их производные различных порядков. Если неизвестные — функции многих переменных, то уравнения называются уравнениями в частных производных, в противном случае при рассмотрении функции только одной независимой переменной уравнения называются обыкновенными дифференциальными уравнениями.
дискретно-детерминированный (конечные автоматы); Теория автоматов — это раздел теоретической кибернетики, в котором изучаются математические модели
— автоматы.
На основе этой теории система представляется в виде автомата, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени.
Автомат можно представить как некоторое устройство (черный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторыевнутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а следовательно, и множество выходных сигналов) являются конечными множествами.
дискретно-стохастический (вероятностные автоматы);
Вобщем виде вероятностный автомат можно определить как дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти в нем и может быть описано статистически.
Применение схем вероятностных автоматов (Р-схем) имеет важное значение для разработки методов проектирования дискретных систем, проявляющих статистически закономерное случайное поведение, для выяснения алгоритмических возможностей таких систем и обоснования границ целесообразности их использования, а также для решения задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.
непрерывно-стохастический (системы массового обслуживания);

Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания
обобщенный, или универсальный (агрегативные системы).
Агрегативная система представляет собой формальную схему общего вида, которую будем называть А- схемой. При агрегативном описании сложный объект (система) разбивается на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие их взаимодействие. Если некоторые из полученных подсистем оказываются в свою очередь еще достаточно сложными, то процесс их разбиения продолжается до тех пор, пока не образуются подсистемы, которые в условиях рассматриваемой задачи моделирования могут считаться удобными для математического описания. В результате такой декомпозиции сложная система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, объединенных в подсистемы различных уровней
6. Дискретно-событийные системы и модели. Схема алгоритма моделирования стохастических дискретно-событийных систем.
В дискретно-событийном моделировании функционирование системы представляется как хронологическая последовательность событий. Событие происходит в определенный момент времени и знаменует собой изменение состояния системы.
Кроме переменных, определяющих состояние системы, и логики, определяющей, что произойдет в ответ на какое-то событие, система дискретно-событийного моделирования содержит следующие компоненты:
Часы
Основной компонент системы, синхронизирующий изменения системы, т.е. возникновение событий.
Список событий
Система моделирования поддерживает по крайней мере один список событий моделирования. Однопоточные системы моделирования, основанные на мгновенных событиях, имеют только одно текущее
событие. В то время как многопоточные системы моделирования и системы моделирования, поддерживающие интервальные события, могут иметь несколько текущих событий. В обоих случаях имеются серьезные проблемы с синхронизацией между текущими событиями.
Генераторы случайных чисел
Дискретно-событийные модели делятся на детерминированные и стохастические, в зависимости от того, каким образом генерируются события и основные характеристики очередей: время наступления событий, длительность обслуживания, количество клиентов, поступающих в очередь в единицу времени. Стохастические дискретно-событийные модели отличаются от моделей Монте-Карло наличием часов.
Статистика
Основные данные, которые собираются в системах дискретно-событийного моделирования:
Средняя занятость (доступность) ресурсов
Среднее количество клиентов в очереди
Среднее время ожидания в очереди
Условие завершения
Условием завершения могут выступать:
•Возникновение заданного события (например, достижение 10-минутного времени ожидания в очереди)
•Прохождение заданного числа циклов по часам системы моделирования
Выполнение событий в ИМ

Операторная схема события Прибытие имеет следующий вид:
1.ПЛАНИРОВАНИЕ СЛЕДУЮЩЕГО ПРИБЫТИЯ В МОМЕНТ ВРЕМЕНИ = ТЕКУЩЕЕ ВРЕМЯ + ВРЕМЯ МЕЖДУ ПРИХОДАМИ;
2.ЕСЛИ ПАРИКМАХЕР “ЗАНЯТ”:
ЧИСЛО_ОЖИДАЮЩИХ := ЧИСЛО_ОЖИДАЮЩИХ + 1; ВОЗВРАТ.
3. ЕСЛИ ПАРИКМАХЕР “СВОБОДЕН”:
ПЕРЕВОД ПАРИКМАХЕРА В СОСТОЯНИЕ “ЗАНЯТ”; ПЛАНИРОВАНИЕ СОБЫТИЯ “ОКОНЧАНИЕ” ОБСЛУЖИВАНИЯ
В МОМЕНТ ВРЕМЕНИ := ТЕКУЩЕЕ ВРЕМЯ + ВРЕМЯ ОБСЛУЖИВАНИЯ; ВОЗВРАТ.
КОНЕЦ
Рассмотрим теперь логику события Конец обслуживания. Операторная схема этого события имеет следующий вид:
1.ЕСЛИ ЧИСЛО_ОЖИДАЮЩИХ БОЛЬШЕ НУЛЯ:
ЧИСЛО_ОЖИДАЮЩИХ := ЧИСЛО_ОЖИДАЮЩИХ - 1; ПЛАНИРОВАНИЕ ОКОНЧАНИЯ ОБСЛУЖИВАНИЯ
В МОМЕНТ ВРЕМЕНИ РАВНЫЙ ТЕКУЩЕМУ ВРЕМЕНИ + ВРЕМЯ ОБСЛУЖИВАНИЯ; ВОЗВРАТ.
2.ЕСЛИ ЧИСЛО_ОЖИДАЮЩИХ РАВНО НУЛЮ:
ПЕРЕВОД ПАРИКМАХЕРА В СОСТОЯНИЕ “СВОБОДЕН”;
ВОЗВРАТ.
КОНЕЦ
7. Основные математические схемы моделирования систем и процессов (D,F,P,Q-схемы)
НЕПРЕРЫВНО-ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ (D-СХЕМЫ)
Обычно в таких математических моделях в качестве независимой переменной, от которой зависят неизвестные искомые функции, служит время t. Тогда математическое соотношение для детерминированных систем в общем виде будет:
где 
 и
и  -- n-мерные векторы
-- n-мерные векторы
 -- вектор-функция, которая определена на некотором (n+1)-мерном
-- вектор-функция, которая определена на некотором (n+1)-мерном  множестве и является непрерывной.
множестве и является непрерывной.
В простейшем случае обыкновенное дифференциальное уравнение имеет вид y’=f(y,t)
ДИСКРЕТНО-ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ (F-СХЕМЫ)
Абстрактно конечный автомат можно представить как математическую схему (F-схему), характеризующуюся шестью элементами:

1.конечным множеством X входных сигналов (входным алфавитом);
2.конечным множеством Y выходных сигналов (выходным алфавитом);
3.конечным множеством Z внутренних состояний (внутренним алфавитом или алфавитом состояний);
4.начальным состоянием z0, z0 Z;
5.функцией переходов φ(z, х);
6.функцией выходов ψ(z, x).
Автомат, задаваемый F-схемой: F=(Z,Y,X,z0, φ ψ) функционирует в дискретном автоматном времени, моментами которого являются такты, т. е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.
Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z0, подавать в некоторой последовательности буквы входного алфавита х(0), x(1), x(2),..., т. е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита у(0), y(1), у(2), ..., образуя выходное слово.
Таким образом, работа конечного автомата происходит по следующей схеме: в каждом f-м такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом в (t+1)-м такте в новое состояние z(t + 1) и выдачей некоторого выходного сигнала.
Чтобы задать конечный F-автомат, необходимо описать все элементы множества F=(Z,Y,X,z0, φ ψ) т. е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов, причем среди множества состояний необходимо выделить состояние z0, в котором автомат находился в момент времени t=0. Существует несколько способов задания работы F-автоматов, но наиболее часто используются табличный, графический и
матричный.
Простейший табличный способ задания конечного автомата основан на использовании таблиц переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы — его состояниям.
При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал хк вызывает переход из состояния z1, в состояние z2, то на графе автомата дуга, соединяющая вершину z1, с вершиной z2, обозначается хк.
Матрица соединений автомата есть квадратная матрица С=||су||, строки которой соответствуют исходным состояниям, а столбцы — состояниям перехода.
ДИСКРЕТНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (Р-СХЕМЫ)
Введем математическое понятие Р-автомата, используя понятия, введенные для F-автомата. Рассмотрим множество G, элементами которого являются всевозможные пары (xi, zj), где хi и zj —элементы входного подмножества X и подмножества состояний
Z соответственно. Если существуют две такие функции ψ и φ, то c их помощью осуществляются отображения G->Z и G->Y, то говорят, что F= (Z, X, Y, ψ, φ) определяет автомат детерминированного типа.
Введем в рассмотрение более общую математическую схему.
Пусть Ф — множество всевозможных пар вида (zk, уj) , где yj — элемент выходного подмножества Y. Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:
появления на выходе сигнала yj если он был в состоянии zs и на его вход в этот момент времени поступил сигнал xi. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В. Тогда четверка элементов P=(Z, X, У, В) называется вероятностным автоматом (Р-автоматом).
НЕПРЕРЫВНО-СТОХАСТИЧЕСКИЕ МОДЕЛИ (2-СХЕМЫ)
Особенности непрерывно-стохастического подхода рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания, которые будем называть Q-схемами.
Системы массового обслуживания представляют собой класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.
В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно изобразить в виде некоторого i-го прибора

обслуживания Пi , состоящего из накопителя заявок Hi, в котором может одновременно находиться 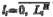 заяaвок, где Li H — емкость i-го накопителя, и канала обслуживания заявок (или просто канала) Кi. На каждый элемент прибора обслуживания Пi поступают потоки событий: в накопитель Hi — поток заявок wi, на канал Ki— поток обслуживании иi.
заяaвок, где Li H — емкость i-го накопителя, и канала обслуживания заявок (или просто канала) Кi. На каждый элемент прибора обслуживания Пi поступают потоки событий: в накопитель Hi — поток заявок wi, на канал Ki— поток обслуживании иi.
Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Поток событий называется однородным, если он характеризуется только моментами поступления этих событий (вызывающими моментами) и задается последовательностью {tn}={0≤t1≤t2…≤tn≤…} где tn— момент наступления и-го события — неотрицательное вещественное число.
Потоком неоднородных событий называется последовательность (tn, fn), где tn — вызывающие моменты; fn — набор признаков события. Например, применительно к процессу обслуживания для неоднородного потока заявок могут быть заданы принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала и т. п.
Различают разомкнутые и замкнутые Q-схемы. В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент, т. е. обратная связь отсутствует, а в замкнутых Q-схемах имеются обратные связи, по которым заявки двигаются в направлении, обратном движению вход-выход.
Для задания Q-схемы также необходимо описать алгоритмы ее функционирования, которые определяют набор правил поведения заявок в системе в различных неоднозначных ситуациях. В зависимости от места возникновения таких ситуаций различают алгоритмы(дисциплины) ожидания заявок в накопителе Нi и обслуживания заявок каналом Ki каждого элементарного обслуживающего прибора Пi, Q-схемы. Неоднородность заявок, отражающая процесс в той или иной реальной системе, учитывается с помощью введения классов приоритетов.
В зависимости от динамики приоритетов в Q-схемах различают статические и динамические приоритеты. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы, т. е. они являются фиксированными в пределах решения конкретной задачи моделирования. Динамические приоритеты возникают при моделировании в зависимости от возникающих ситуаций. Исходя из правил выбора заявок из накопителя Hi на обслуживание каналом Ki можно выделить относительные и абсолютные приоритеты.
Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Hi ожидает окончания обслуживания предшествующей заявки каналом Кi, и только после этого занимает канал.
Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Нi, прерывает обслуживание каналом Кi заявки с более низким приоритетом и сама занимает канал (при этом вытесненная из Ki заявка может либо покинуть систему, либо может быть снова записана на какое-то место в Hi) .
Весь набор возможных алгоритмов поведения заявок в Q-схеме можно представить в виде некоторого оператора алгоритмов поведения заявок А. Таким образом, Q-схема, описывающая процесс функционирования системы массового обслуживания любой сложности, однозначно задается в виде Q=<W, U, H, Z, R, А).
При ряде упрощающих предположений относительно подмножеств входящих потоков W и потоков обслуживания U (выполнение условий стационарности, ординарности и ограниченного последействия) оператора сопряжения элементов структуры R (однофазное одноканальное обслуживание в разомкнутой системе), подмножества собственных параметров Н (обслуживание с бесконечной емкостью накопителя), оператора алгоритмов обслуживания заявок А (бесприоритетное обслуживание без прерываний и блокировок)для оценки вероятностно-временных характеристик можно использовать аналитический аппарат, разработанный в теории массового обслуживания.
8. Случайные потоки однородных событий: основные определения и свойства.
Поток событий — это последовательность однородных событий, наступающих одно за другим в случайные промежутки времени. На оси времени эти события выглядят, как показано на рисунке
где τj — интервал между событиями (случайная величина); tсi — момент совершения i-го события (отсчитывается от t = 0); Tн — время наблюдения.
Интенсивность потока λ — это среднее число событий в единицу времени. Интенсивность потока можно рассчитать экспериментально по формуле: λ = N/Tн, где N — число событий, произошедших за время наблюдения Tн.
Если интервал между событиями τj равен константе или определен какой-либо формулой в виде: tj = f(tj – 1), то поток называется детерминированным. Иначе поток называется случайным.
Случайные потоки бывают:
•ординарные: вероятность одновременного появления двух и более событий равна нулю;
•стационарные: частота появления событий λ(t) = const(t);
•без последействия: вероятность появления случайного события не зависит от момента совершения предыдущих событий.
Наиболее часто при моделировании случайных процессов используются следующие законы распределения: - равномерный;

-нормальный;
-экспоненциальный;
-бета - закон.
а) равномерное распределение
Если некоторая числовая характеристика моделируемого процесса с равной вероятностью может принять любое значение из заданного допустимого интервала, для ее описания используется равномерный закон распределения. Параметрами в данном случае являются середина и ширина допустимого интервала значений.
б) нормальное распределение
Нормальный закон распределения используется, если значения характеристики группируются около среднего (математического ожидания). Чем дальше значение от математического ожидания, тем меньше вероятность, что характеристика примет это значение.
Параметрами в данном случае являются математическое ожидание и дисперсия задаваемой характеристики. Дисперсия выбирается так, чтобы соблюдалось условие: вероятность того, что случайная характеристика примет значение, отличающееся от математического ожидания больше, чем на величину утроенной дисперсии, практически равна нулю. В случае, ели моделируемая характеристика не должна принимать отрицательных значений, параметры распределения должны удовлетворять условию m - 3σ >= 0, где m и σ - соответственно математическое ожидание и дисперсия случайной характеристики.
в) суперпозиция потоков событий и экспоненциальное распределение
Рассмотрим, например, входной поток пассажиров на станцию метрополитена. Событием является приход очередного пассажира. Потоком событий является последовательность посещений метро отдельным пассажиром. Интервалы между приходами являются случайными числами. Если эти потоки для очень большого числа N пассажиров спроектировать на общую ось времени, то интервал между двумя соседними событиями (приходами пассажиров на остановку), возможно, принадлежащих разным потокам, будет являться случайной величиной, распределение которой, по теореме о суперпозиции потоков случайных событий, подчиняется экспоненциальному закону. На рис. 3 представлена схема суперпозиции потоков событий. События в различных исходных потоках происходят независимо друг от друга.
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
0 |
|
|
t |
|||||
|
|
|
||||||
Рис. 3. Схема суперпозиции потоков случайных событий
Другим примером суперпозиции потоков событий является выход из строя какого-либо достаточно сложного технического устройства. Каждая деталь имеет свой срок безотказной работы, по истечении которого ее приходится чинить. Какая деталь выйдет из строя следующей после очередного ремонта устройства, предсказать невозможно. Таким образом, интервал между поломками является случайной величиной, имеющей экспоненциальное распределение.
Задаваемым параметром в данном случае является математическое ожидание характеристики, которое совпадает с дисперсией.
Важной характеристикой экспоненциального распределения является также отсутствие последействия. Пусть, например, случайной характеристикой является интервал прихода автобуса на остановку. Если этот интервал задать с помощью экспоненциального распределения, то время, прошедшее с момента прихода предыдущего автобуса, никак не влияет на оставшееся время ожидания.
г) бета-распределение
Это распределение используется в случае, если случайная характеристика имеет конечный интервал допустимых значений и некоторое наиболее вероятное значение. Параметрами распределения являются минимальное, наиболее вероятное и максимальное значения характеристики. Наиболее вероятное значение, вообще говоря, может совпадать с минимальным или максимальным.
Пуассоновский поток — это ординарный поток без последействия.
Как ранее было указано, вероятность того, что за интервал времени (t0, t0 + τ) произойдет m событий, определяется из закона Пуассона:

где a — параметр Пуассона.
Если λ(t) = const(t), то это стационарный поток Пуассона (простейший). В этом случае a = λ · t. Если λ = var(t), то это нестационарный поток Пуассона.
Для простейшего потока вероятность появления m событий за время τ равна:
Вероятность непоявления (то есть ни одного, m = 0) события за время τ равна:
Вероятность появления хотя бы одного события (PХБ1С) вычисляется так:
так как PХБ1С + P0 = 1 (либо появится хотя бы одно событие, либо не появится ни одного, — другого не дано).
9. Марковские процессы: определения и классификация
Ма|рковскии} проце|сс — случаи} ныи} процесс, эволюция которого после любого заданного значения временно|го параметра t не зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано
Более доступно: случайный процесс, протекающий в системе S с дискретными состояниями S1,S2,… ,Si,…, называется Марковским, если для любого момента времени t0 вероятность каждого из состояний системы в будущем (при t > t0) зависит только от её состояния в настоящем (при t = t0) и не зависит от того, когда и как она пришла в это состояние; т.е. не зависит от ее поведения в прошлом (при t < t0).
Из определения Марковской цепи следует, что для нее вероятность перехода системы S в состояние Sj на (k+1)-м шаге зависит только от того, в каком состоянии Si находилась система на предыдущем k-м шаге и не зависит от того, как она вела себя до этого k-шага.
Pij(k) = P {S(k) = Sj / S(k-1) = Si } – условная вероятность перехода
Pij – вероятность переходов
Pjj – задержка
Итак, марковский процесс удобно задавать графом переходов из состояния в состояние. Мы рассмотрим два варианта описания марковских процессов — с дискретным и непрерывным временем.
В первом случае переход из одного состояния в другое происходит в заранее известные моменты времени — такты (1, 2, 3, 4, …). Переход осуществляется на каждом такте, то есть исследователя интересует только последовательность состояний, которую проходит случайный процесс в своем развитии, и не интересует, когда конкретно происходил каждый из переходов.
Во втором случае исследователя интересует и цепочка меняющих друг друга состояний, и моменты времени,
вкоторые происходили такие переходы.
Иеще. Если вероятность перехода не зависит от времени, то марковскую цепь называют однородной. Марковская цепь называется однородной, если вероятности переходов не зависят от шага.
Чтобы найти вероятности Pi(k), недостаточно знать матрицу переходов вероятностей, нужно ещё знать начальное распределение вероятностей:
P1(0), P2(0), …. , Pi(0), …, Pn(0).
Найдем распределение вероятностей на k шаге:
В момент времени k = 0 система находится в i состоянии
Hi : Pi(0) = P{S(0) = Si}, тогда Pij = P{S(1) = Sj / S(0) = Si}

По формуле полной вероятности получим:
В момент времени k = 1 система находится в i состоянии
Hi : Pi(1) = P{S(1) = Si}, тогда Pij = P{S(2) = Sj / S(1) = Si}
По формуле полной вероятности получим:
Таким образом мы выразили распределение вероятностей на втором шаге через распределение на первом шаге и матрицу || Pij||. Переходя таким же образом от k=2, k=3, … , получим рекуррентную формулу:
10. Марковские цепи с непрерывным временем. Построение системы уравнений Колмогорова для определения вероятностей состояний процесса.
Пример графа марковского процесса с непрерывным временем
Теперь каждый переход характеризуется плотностью вероятности перехода λij. По определению:
При этом плотность понимают как распределение вероятности во времени.
Переход из i-го состояния в j-е происходит в случайные моменты времени, которые определяются интенсивностью перехода λij.
Зная интенсивность λij появления событий, порождаемых потоком, можно сымитировать случайный интервал между двумя событиями в этом потоке.
где τij — интервал времени между нахождением системы в i-ом и j-ом состоянии.
Далее, очевидно, система из любого i-го состояния может перейти в одно из нескольких состояний j, j + 1, j + 2, …, связанных с ним переходами λij, λij + 1, λij + 2, ….
В j-е состояние она перейдет через τij; в (j + 1)-е состояние она перейдет через τij + 1; в (j + 2)-е состояние она перейдет через τij + 2 и т. д.
Ясно, что система может перейти из i-го состояния только в одно из этих состояний, причем в то, переход в которое наступит раньше.
Поэтому из последовательности времен: τij, τij + 1, τij + 2 и т. д. надо выбрать минимальное и определить индекс j, указывающий, в какое именно состояние произойдет переход.
Рассмотрим однородный процесс, т.е. процесс, в котором lij не зависит от t .
Пусть система в некоторый момент времени t находится в состоянии Хm с вероятностью Pm(t) . Придадим величине t малое приращение Dt и найдем вероятность того, что в момент времени t + Dt система будет находиться в том же состоянии Хm . Это событие может произойти следующим образом:
1)в момент t система уже была в состоянии Хm и за время Dt не вышла из этого состояния или:
2)в момент t система была в состоянии Хi  , а за время Dt перешла в состояние Хm . Вероятность первого варианта вычисляется так: Pm(t) умножается на условную вероятность того, что
, а за время Dt перешла в состояние Хm . Вероятность первого варианта вычисляется так: Pm(t) умножается на условную вероятность того, что
система за Dt не перейдет ни в какое другое состояние Хi (i?m) . Так как события, состоящие в переходе за время Dt из Хm в Хi , несовместны, то вероятность того, что осуществится один из этих переходов, равна сумме их вероятностей, т.е.
