
Исследование операций и методы оптимизации
.pdf
Таблица 3 Таблица 4
|
1 |
Х1 |
Х2 |
|
|
1 |
Х1 |
У2 |
|||||||||||
L’ |
0 |
|
1 |
|
1 |
|
|
|
|
L’ |
-1 |
|
1 |
|
|
|
1 |
|
|
|
-1 |
0 |
|
|
1 |
|
|
-4 |
|
|
-1 |
0 |
|||||||
У1 |
2 |
|
-1 |
|
1 |
|
|
|
|
У1 |
1 |
|
-1 |
|
|
|
1 |
|
|
|
|
|
1 |
1 |
|||||||||||||||
|
-1 |
0 |
|
|
|
4 |
|
|
0 |
||||||||||
У2 |
-1 |
|
0 |
|
-1 |
|
|
|
|
Х2 |
1 |
|
0 |
|
|
|
-1 |
|
|
1 |
0 |
-1 |
0 |
||||||||||||||||
|
|
|
0 |
|
0 |
||||||||||||||
У3 |
4 |
|
1 |
|
0 |
|
|
|
|
У3 |
4 |
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
4 |
|
|
1 |
|
0 |
|||||||
|
|
0 |
|
0 |
0 |
|
|
||||||||||||
2/1=2; -1/-1=1(min)
В таблице 4 получено опорное решение: х1=у2=0, y1=1, х2=1, y3=4, L’= -1.
В таблице 4 выполняем алгоритм отыскания оптимального решения:
Таблица 5
|
1 |
У3 |
У2 |
|||||
L’ |
-5 |
|
-1 |
|
1 |
|
|
|
|
-5 |
-1 |
|
-1 |
||||
У1 |
5 |
|
1 |
|
1 |
|
|
|
5 |
1 |
1 |
||||||
|
||||||||
Х2 |
1 |
|
0 |
|
-1 |
|
|
|
|
|
1 |
||||||
|
5 |
1 |
|
|||||
Х1 |
4 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|||||
|
|
0 |
|
0 |
0 |
|||
Таблица 6
|
1 |
У3 |
|
У1 |
|||
L’ |
-10 |
|
-2 |
|
-1 |
|
|
|
|
|
|
|
|
|
|
У2 |
5 |
|
1 |
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Х2 |
6 |
|
1 |
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Х1 |
4 |
|
1 |
|
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
В таблице 6 получено оптимальное решение:
у3 = у1= 0, у2= 5, х2= 6, х1= 4, L’= -10, Lmax= 10.
Так как в данной задаче всего две свободных переменных, то можно рассмотреть ее геометрически на плоскости (рис. 11).
28
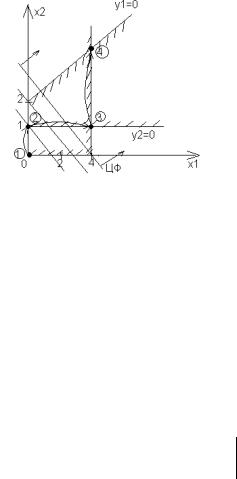
Так как у1=0, у3=0, то решение находится в точке, в которой выполняются равенства: х1-х2+2=0 и
4 -х1 = 0.
На рисунке 11 показана последовательность перехода от вершины к вершине в соответствии с работой алгоритма сим- плекс-метода. Цифрами обозначены соответствующие симплекс-
таблицы. Рис. 11
2.7. Алгоритм получения первого базисного решения с использованием симплекс – процедуры
(метод искусственного базиса)
Выше было показано, что алгоритмы симплекс-метода требуют, чтобы исходная система ограничений-равенств была приведена к базису, т.е. какиенибудь базисные переменные должны быть выражены через свободные. Оказывается, что первый базис можно так же получить, используя алгоритм сим- плекс-метода. Для этого для каждого ограничения-равенства вводится искусственная переменная zi (i=1,m). Каждое ограничение-равенство
βi - (gi1 x1 + ... + gin xn) = 0
формально записывается так:
zi =βi - (gi1 x1 + ... + gin xn), i=1,m ,
т.е. переменные zi тождественно равны нулю. Последнее равенство определяет так называемый искусственный базис.
Вводим в рассмотрение дополнительную целевую функцию
Lo = z1 + z2 + ... + zm → min ,
для чего суммируем коэффициенты при переменных xj всех равенств zi и получаем ОЗЛП, готовую для решения симплекс-методом.
Решая эту задачу на основе вышеприведенных алгоритмов последовательно выводим из базиса все искусственные переменные zi. При этом, как только переменная zr становится свободной, то столбец zr исключается из симплекс-таблицы.
Пример. Пусть исходную задачу ЛП мы привели к форме ОЗЛП и получили систему ограничений-равенств
29

x1 + 2 x2 = 4
x1 - x2 + 2 x3 = 2
Найдем первый базис, т.е. разрешим базисные переменные (их всего будет 2) относительно свободных (n-m=3-2=1). Для этого запишем
z1 = 4 - (x1 + 2 x2),
z2 = 2 - (x1 - x2 + 2 x3), |
(2.10) |
Lo = z1 + z2 = 6 - (2 x1 + x2 + 2 x3) →
= z1 + z2 = 6 - (2 x1 + x2 + 2 x3) → min.
min.
Запишем симплекс-таблицу
Таблица 7
|
1 |
X1 |
X2 |
X3 |
|
L0 |
6 |
2 |
1 |
2 |
|
-4 |
-2 |
2 |
-4 |
||
|
|||||
Z1 |
4 |
1 |
2 |
0 |
|
-2 |
-1 |
1 |
-2 |
||
|
|||||
Z2 |
2 |
(1) |
-1 |
2 |
|
2 |
1 |
-1 |
2 |
||
|
В таблице 7 находим генеральный элемент по алгоритму нахождения оптимального решения, получаем пару для симплекс-преобразования и переходим к таблице 8, в которой исключаем столбец z2.
Таблица 8
|
1 |
X2 |
X3 |
|
L0 |
2 |
3 |
-2 |
|
-2 |
-1 |
2 |
||
|
||||
Z1 |
2 |
(3) |
-2 |
|
2/3 |
1/3 |
-2/3 |
||
|
||||
Х1 |
2 |
-1 |
2 |
|
2/3 |
1/3 |
-2/3 |
||
|
В таблице 8 находим генеральный элемент и пару z1 ↔ x2, переходим к таблице 9.
30
Отформ
польски
Отформ
польски
Отформ
польски
Отформ
польски
Отформ
польски
Отформ
польски
Отформ
польски
Отформ
польски
Таблица 9
|
1 |
X3 |
L |
0 |
0 |
|
|
|
|
|
|
X2 |
2/3 |
-2/3 |
|
|
|
|
|
|
X1 |
8/3 |
4/3 |
|
|
|
|
|
|
Таблица 9 соответствует оптимальному решению вспомогательной задачи (2.10) и дает выражение базисных переменных x1, x2 относительно свободной переменной x3, а именно:
x2 = 2/3 + 2/3x3;
x1 = 8/3 - 4/3x3.
Теперь можно приступать к выполнению симплекс-алгоритма, записав вместо строки Lo целевую функцию задачи, выраженную через свободные переменные. Чтобы такая запись получалась автоматически можно в таблицу 7 кроме строки Lo записать строку целевой функции исходной ОЗЛП и выполнять описанный выше алгоритм, помня, что генеральный элемент не может быть ни в строке Lo, ни в строке ЦФ.
2.8. Вырожденная задача ЛП
При использовании симплекс-метода некоторые свободные члены могут быть равны нулю. Это значит, что в вершине, которой соответствует CТ, равны нулю не k переменных, а больше (равна нулю и базисная). В этом случае при выборе генерального элемента отношение bi/aij будет минимальным именно для этой строки. Ясно, что соответствующую свободную переменную увеличить никак нельзя и целевая функция при переходе в новую вершину не меняется, т.к. мы остаемся фактически в этой же вершине, хотя формально перешли в новую.
Такая задача называется вырожденной задачей. Вырождение отрицательно сказывается на эффективности вычисления. Признаком вырожденности является равенство 0 некоторых свободных членов. В этом случае может произойти 2 отрицательных явления:
1.«Пробуксовка». Переходим в новую вершину, где равна нулю другая совокупность переменных, а на самом деле остаемся в той же точке. Значение ЦФ не меняется.
31
2.«Зацикливание» алгоритма. Через некоторое количество операций мы
можем прийти к первоначальной таблице, следовательно, если алгоритм не менять, то зацикливаемся.
Существует несколько способов борьбы с зацикливанием:
•Использование степени свободы алгоритма. Например, если в алгоритме сказано: «берем первый по порядку…» - то, если обнаруживается зацикливание, можно взять «второй по порядку». Аналогично, если сказано «берем любой…».
•«Зашумление» коэффициентов задачи ЛП. Прибавляем матрицу малых случайных величин к матрице А. Получаем А + ξ, где А – матрица коэффициентов; ξ – матрица очень малых случайных величин. Тогда матрица коэффициентов СТ не будет содержать одинаковых чисел и после вычислений появление нулей будет маловероятным. Подробнее этот сложный вопрос освещен в специальной литературе.
2.9. Двойственная задача ЛП
Важным вопросом анализа полученного решения ЛП является анализ чувствительности решения к параметрам модели (коэффициентам целевой функции, свободным членам ограничений, коэффициентам аij). Теория этого вопроса тесно связана с так называемой двойственной задачей ЛП. Двойственная задача ЛП получается из прямой и она имеет физический смысл, когда прямая задача – задача об использовании ресурсов. Имеются ресурсы m типов в количестве b1, … bm. Для изготовления одного изделия j – го типа расходуется aij сырья i-го типа. Каждое j – е изделие продается по цене сj. Ставится задача максимизации стоимости проданных изделий.
n |
|
||
L = ∑cj xj → max, |
(2.11) |
||
j=1 |
|
||
n |
|
||
∑aij xj ≤ bj , i = |
1,m |
, |
(2.12) |
j−1
xj ≥ 0, j
Можно рассмотреть эту проблему по-другому. Пусть некоторые величины ∆i – стоимости единицы i – го ресурса. Нужно определить эти стоимости так, чтобы выполнялись неравенства, выражающие то, что стоимость затраченного ресурса на j – е изделие была бы не меньше стоимости изделия и при этом общие затраты на ресурсы были минимальны.
m |
|
L* = ∑bi i → min, |
(2.13) |
i=1
32

m |
|
∑αij i ≥ cj , j =1,..., n |
(2.14) |
i=1
Задача (2.13), (2.14) называется двойственной по отношению к задаче (2.11), (2.12) Она получается из прямой (2.11), (2.12) так: коэффициенты целевой функции двойственной задачи – это правые части прямой задачи и наоборот; а коэффициенты aij – суммируются по другому индексу (матрица коэффициентов двойственной задачи это транспонированная матрица прямой задачи). Направление оптимизации целевой функции меняется на противоположное.
Основное свойство задачи ЛП: оптимальные значения целевой функции прямой и двойственной задачи ЛП совпадают:
n |
= ∑bi |
|
L*опт = ∑c j x*j |
*i |
|
j=1 |
i=1 |
|
Оптимальное решение задачи ЛП находится в седловой точке:
max L по хj = min L* по ∆i.
Существует и двойственный симплекс–метод решения задачи ЛП, который в ряде случаев эффективнее прямого [1, 10].
Экономический смысл двойственной задачи: какова цена единицы каждого ресурса ∆i, чтобы при заданных количествах ресурсов bi и стоимости единицы продукции сj обеспечить минимум общей стоимости затрат.
∆i называется двойственной оценкой или теневой ценой. Если решение прямой задачи найдено, то ∆i – есть коэффициенты, стоящие в строке L в последней оптимальной CТ.
Если ∆i > 0, то она показывает, насколько увеличивается значение целевой функции прямой задачи, если соответствующие запасы сырья i – го типа увеличиваются на единицу.
Соответствующая дополнительная переменная yi при этом равна нулю. Это означает, что i – е ограничение выполняется точно (как равенство) и весь ресурс bi тратится полностью.
При малом изменении коэффициентов модели оптимальное решение задачи ЛП не меняется, такое свойство называется устойчивостью. На рисунке 12 показано, что для ЦФ1 решением является точка А, для ЦФ3 *(при малом изменении коэффициентов cj) также точка А, а для ЦФ2 решением уже будет точка В.
33
Существуют специальные программы, которые позволяют проанализировать пределы изменения коэффициентов cj , при которых оптимальное решение не изменяется, а значение целевой функции меняется. Аналогично проводится анализ по правым частям bi.
Современные алгоритмы ЛП способны с использованием современных компьютеров решать задачи ЛП очень большой размерности. Многие из них учитывают архитектуру компьютера.
Наиболее широко известны блочные методы ЛП. При большой размерности матрица А будет содержать много нулей. В этом случае задачу можно решать по блокам. Вот почему параметрами сложности решаемой задачи ЛП являются: число переменных, число ограничений и число ненулевых коэффициентов ограничений. Число итераций симплексметода, за которое находится решение в большей степени зависит от числа ограничений. Современные программы ЛП имеют удобный интерфейс, позволяющий моделировать и решать небольшие задачи в удобной «математической» или табличной форме. Для решения задач ЛП большой размерности используются режимы работы с крупными базами исходных данных. Например, программа LINDO, а также приложение «Поиск решения» (SOLVER) про-
граммы Microsoft EXCEL.
34

3.ТРАНСПОРТНЫЕ ЗАДАЧИ (ТЗ)
3.1.Математическая модель ТЗ по критерию стоимости
Симплекс–метод является общим для любой задачи ЛП. Но существуют специальные задачи ЛП, которые имеют более простой и наглядный способ решения.
Постановка транспортной задачи:
Имеется m пунктов А1…Аm отправления, в каждом из которых сосредоточено определенное количество груза (a1…am). Груз однородный, величина ai называется запасом. Имеются n пунктов назначения B1…Bn, где требуется количество груза (b1…bn); величина bi - заявка. Известна стоимость перевоз-
ки cij - из i – го пункта в j – й пункт.
Требуется так перевезти грузы, чтобы запасы не были превышены, заявки выполнены, и общая стоимость перевозки была бы минимальной.
Введем дополнительное требование – так называемое условие правиль-
|
|
m |
|
|
|
n |
|
||
ного баланса: ∑ai =∑bj |
|
||||||||
|
|
i=1 |
|
|
|
j=1 |
|
||
Модель: |
|
|
|
|
|
||||
xij |
- количество груза, перевозимого из i – го в j – й. |
|
|||||||
|
m |
n |
|
|
|
|
|
||
L = ∑∑cij xij |
→ min , |
(3.1) |
|||||||
|
i=1 |
j=1 |
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
∑xij =ai ,i = |
1, m |
|
|
, |
(3.2) |
||||
j=1 |
|
|
|
|
|
|
|
||
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑xij =bj , j =1, n |
|
|
|||||||
i=1 |
|
|
|
|
|
|
|
|
|
xij |
> 0, i, j |
|
|
|
|
|
|||
m |
|
n |
|
|
|
|
|
||
∑ai =∑b j |
|
|
|
|
|
||||
i=1 |
|
j=1 . |
|
|
|
|
(3.3) |
||
Особенности модели ТЗ:
1.Наличие условия баланса (3.3) приводит к тому, что задача ТЗ всегда
 имеет решение.
имеет решение.
2.Просуммировав левые части (3.2), получим (3.3), следовательно, одно уравнение в (3.2) линейно зависимо, значит ранг системы (3.2) будет (n+m – 1).
35
Отформа
Отступ: Сл
17,85 пт,
Уровень: 1 нумерации Начать с: 1 слева + Вы + Табуляц Отступ: 18
3.Коэффициенты при переменных в (3.2) все равны единице.
4.Подсчитаем число свободных и базисных переменных. Всего переменных m×n. Базисных (m+n -1). Свободных переменных будет m×n- m-n+1 =k, … k=(m-1)×(n-1). Т.е. практически все переменные свободные. Т.к. ТЗ является задачей ЛП, то в оптимальном решении все свободные переменные должны быть равны нулю, т.е. большинство маршрутов не будут задействованы. Если m=100 и n=100, всего маршрутов (переменных) 10 000, но не более 199 будут задействованы.
3.2. Нахождение опорного плана транспортной задачи
Все условия транспортной задачи можно записать в так называемой транспортной таблице.
В ней выполняются и все необходимые вычисления. Пример:
Стоимость перевозки
Перевозка (кол-во единиц в маршруте)
|
|
Таблица 10 |
|
|
I |
B1 |
B2 |
B3 |
ai |
A1 |
4 |
1 |
3 |
11 |
|
5 |
6 |
|
|
A2 |
2 |
5 |
2 |
7 |
|
|
7 |
|
8 |
A3 |
3 |
7 |
4 |
|
|
|
3 |
5 |
|
A4 |
2 |
4 |
5 |
4 |
bj |
|
|
4 |
30 |
5 |
16 |
9 |
Назовем xij «перевозкой». РешениеТЗ, такжекакиЛПсостоитиз2 этапов:
1.Находится опорный план, т.е. допустимый план, соответствующий условию «вершины». В нем отличных от нуля перевозок не более (m+n-1).
2.Путем последовательного перехода от одного опорного плана к другому получаем оптимальный план.
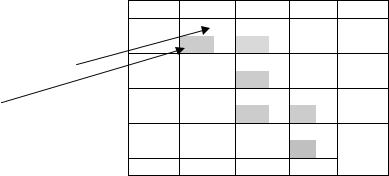
Метод «северо-западного угла» (СЗУ) для нахождения опорного плана ТЗ Он заключается в заполнении плана перевозок, начиная с самих верхних (северных) пунктов отправления за счет самых левых (западных) пунктов на-
значения. Величина перевозки определяется выражением:
xij = min{ai′,b′j }, |
(3.4) |
36
где ai' и b'i - остатки запаса и заявки после предыдущей итерации. Этот
способ обеспечивает линейную независимость столбцов. Свойство допустимого плана: сумма перевозок по строке равна запасу, а по столбцу – заявке. План называется невырожденным, если отличных от нуля перевозок ровно m+n -1. В вышеприведенном примере m + n – 1 = 4 +4 – 1 = 7=7, т.е. план невырожденный.
Выполненные действия показаны в таблице 10 Определим стоимость плана:
L=4×5+5×4+1×4+2×2+3×1+5×3+5×2=76.
Часто бывают такие транспортные задачи, где количество ненулевых перевозок (базисных клеток) меньше, чем m + n – 1.
Пример:
|
|
|
|
Таблица 11 |
|
Базисных клеток 4, а должно быть 5. |
|||||
|
|
|
|
|
Задача вырожденная. Будем дополнять |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
B2 |
|
B3 |
ai |
|
план до невырожденного: в опреде- |
|||
A1 |
3 |
|
|
4 |
|
|
(0) |
|
7 |
+0 |
ленных местах проставим символиче- |
A2 |
|
|
|
|
|
|
1 |
|
1 |
|
скую бесконечно малую величину (0), |
|
|
|
|
|
|
|
|
чтобы выполнялась линейная незави- |
|||
A3 |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
симость столбцов и условие невырож- |
|||
bj |
3 |
|
4 |
|
3 |
|
|
|
|||
|
|
|
|
|
денности. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы автоматически определять место для дополнения плана будем избавляться от вырожденности в процессе заполнения плана в соответствии с выражением (3.4). Вырожденность появляется тогда, когда в формуле (3.4) будет ai\=bj\ . В этом случае будем считать, что в строке ai\=ai\ + (0).
Метод минимального элемента В методе СЗУ мы не использовали стоимость перевозок. Существуют
методы, которые позволяют получить первый план сразу близким к оптимальному (т.е. с достаточно малой общей стоимостью перевозок).
Метод минимального элемента состоит в том, что порядок заполнения плана соответствует возрастанию стоимости. Но при этом запас исчерпывается полностью, т.е. перевозка ставится в соответствии с формулой (3.4) в клетке с минимальной стоимостью в строке, если не исчерпали запас, или в столбце, если не выполнили заявку.
Метод не обязательно гарантирует лучшее решение, чем метод С ЗУ, но, как правило, дает лучшие результаты.
Способ борьбы с вырождением такой же, как и в предыдущем методе. Пример: Начинаем с самого дешевого маршрута (А1В4), далее в столбце
В4 ищем самый дешевый (А4В4), затем в строке А4 минимальная стоимость 2 в маршруте (А4В2) и т.д.
37
