
- •I курс, I семестр Линейная алгебра
- •Теоретический курс
- •1.Матрицы. Виды матриц.
- •2.Действия над матрицами.
- •7.Метод Крамера.
- •8.Матричный метод.
- •9.Метод Гаусса.
- •Примеры решения задач.
- •Расчётно-графическая работа №1.
- •Векторная алгебра. Аналитическая геометрия.
- •Теоретический курс.
- •Аналитическая геометрия
- •Примеры решения задач.
- •Расчетно-графическая работа №2.
7.Метод Крамера.
Метод Крамера применяется при решении систем, в которых число уравнений и количество неизвестных совпадают:
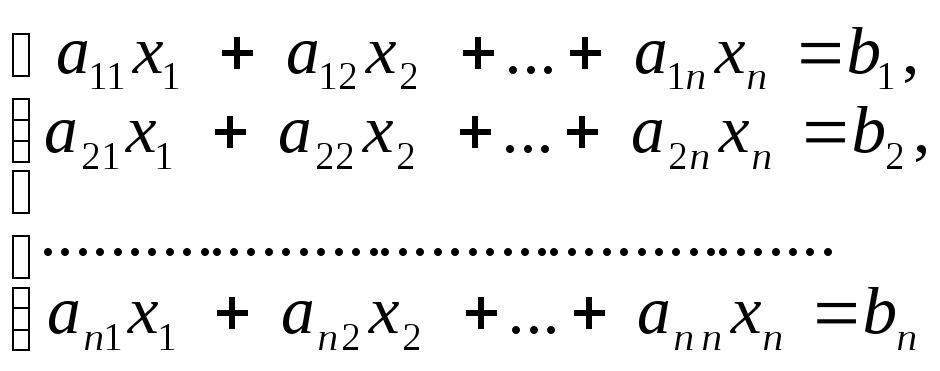
Составим главный определитель системы и вычислим его.
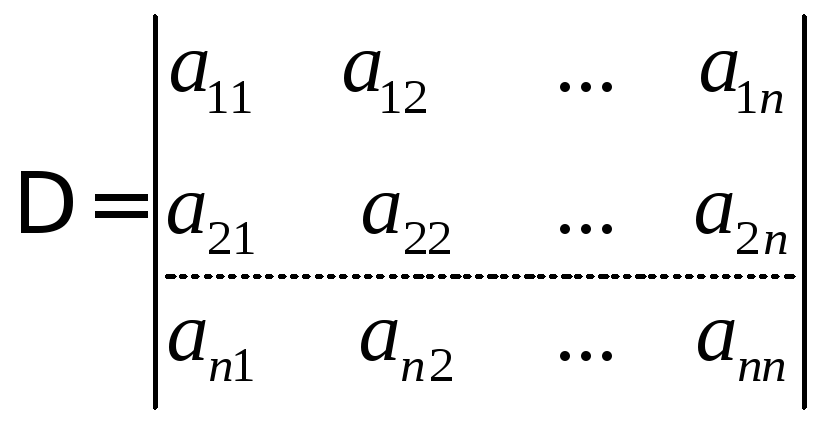
Составим
и вычислим вспомогательные определители
![]() ,где
i
=1,2,…,n, путем замены i-го столбца столбцом
свободных членов.
,где
i
=1,2,…,n, путем замены i-го столбца столбцом
свободных членов.
Решение системы линейных уравнений находится по формулам Крамера:
xi=![]() где
i=1,2,…,n,
где
i=1,2,…,n,
![]()
8.Матричный метод.
Рассмотрим систему n линейных уравнений с n неизвестными:
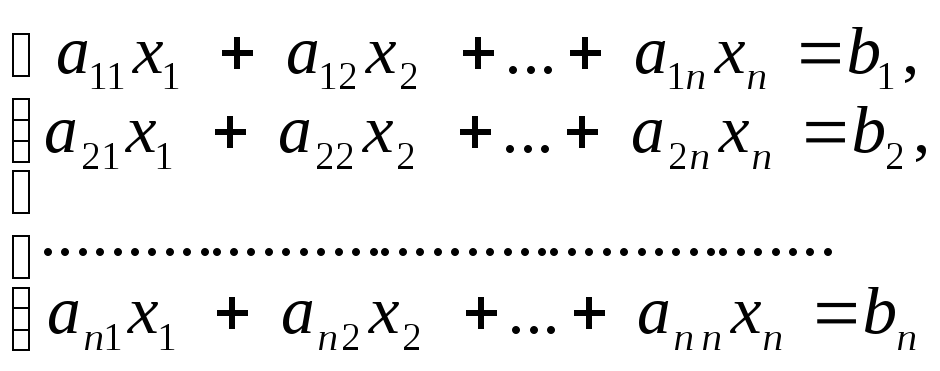
Введем матрицы:
1.Основная
матрица системы
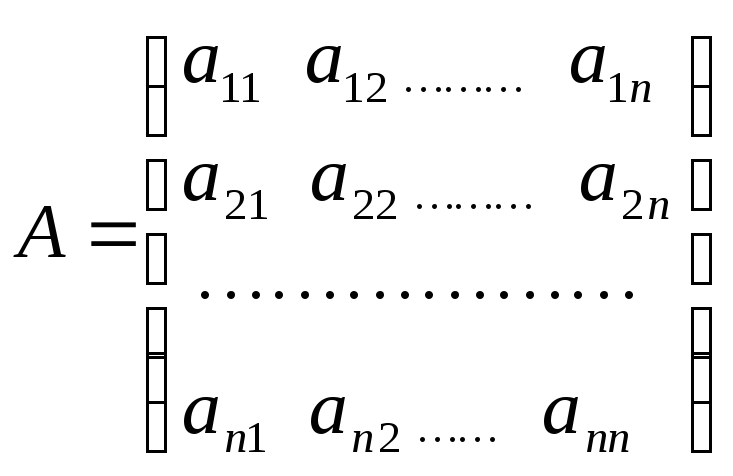
2.Вектор-столбец
неизвестных
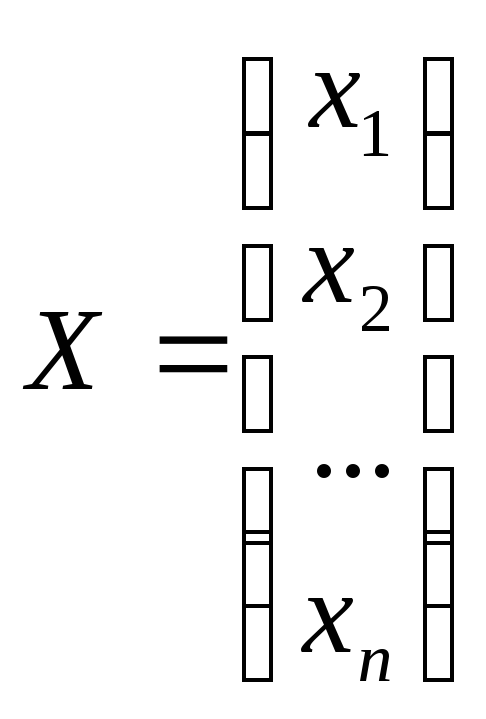
3.Вектор-столбец
свободных членов

Запишем систему в матричном виде АХ=В.
Решение
матричного уравнение имеет вид: Х=А-1×В,
если
![]()
9.Метод Гаусса.
Целью метода Гаусса является приведение матрицы системы к треугольному виду, используя элементарные преобразования:
1.Умножение некоторого уравнения на число, не равное нулю.
2.Прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число.
3.Перестановка местами двух уравнений системы.
Суть метода состоит в следующем.
Пусть дана система m линейных уравнений с n неизвестными
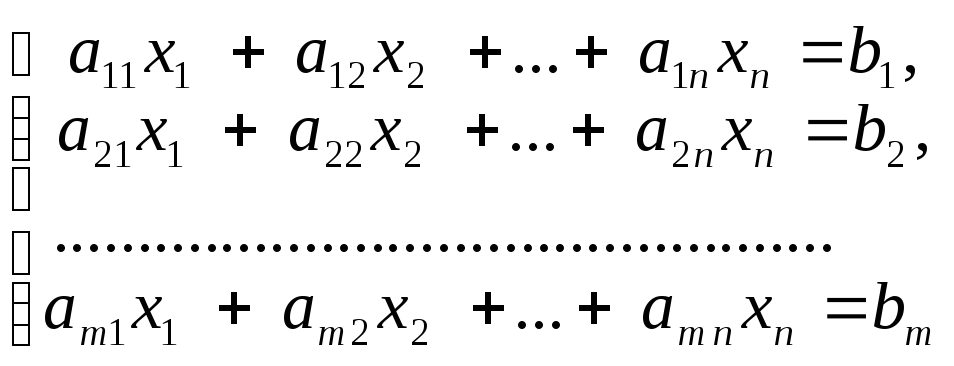
Запишем расширенную матрицу системы
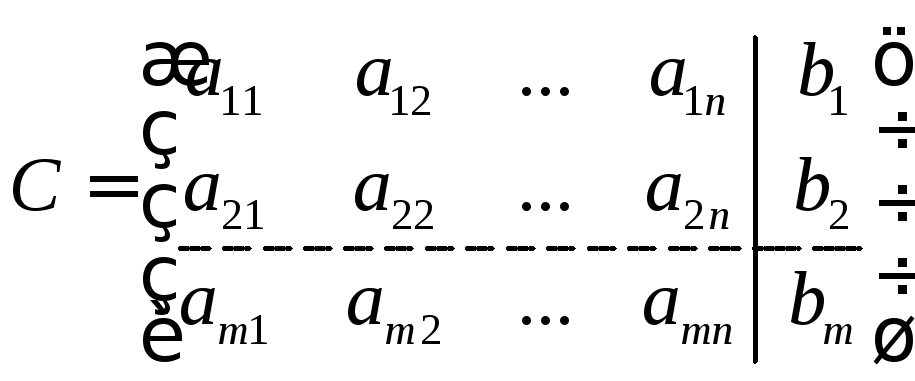
Пусть а11 ≠ 0, в противном случае всегда можно принять за первое уравнение то, в котором коэффициент при хi отличен от нуля и перенумеровать неизвестные.
1.Исключим элементы ai1 , i=2,…m, умножением первой строки на выражение ( - ai1/ a11), i=2,…m и прибавлением ее к последующим строкам. Здесь возможны случаи
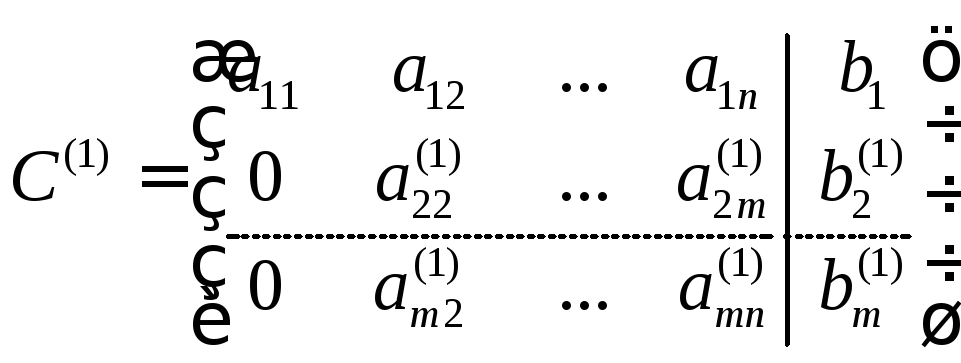
а) получилась строка расширенной матрицы С(1) , у которой все элементы aij(1), i=2,…m, j=2,…n равны нулю, а хотя бы один соответствующий элемент bi(1)≠0. Тогда исходная система несовместима.
б) только первая строка матрицы С(1) ненулевая. Тогда исходная система состоит из одного уравнения. Если в этом уравнении все коэффициенты, за исключением a11 равны нулю, то исходная система имеет единственное решение. В противном случае система неопределённая.
в) среди коэффициентов ai1(1) существует хотя бы один отличный от нуля. Тогда следует перейти к очередному шагу.
2. Пусть a22(1) ≠0 . В матрице С(1) исключим элемент ai2, i=3,…m. Получим матрицу вида
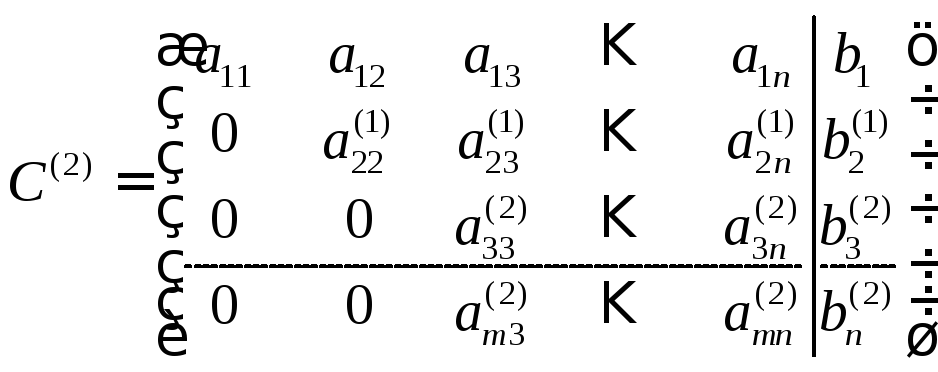
Здесь возможны случаи а, б, в. Если имеет место третий случай, то следует перейти к следующему шагу и т.д.
Необходимо привести матрицу к виду:
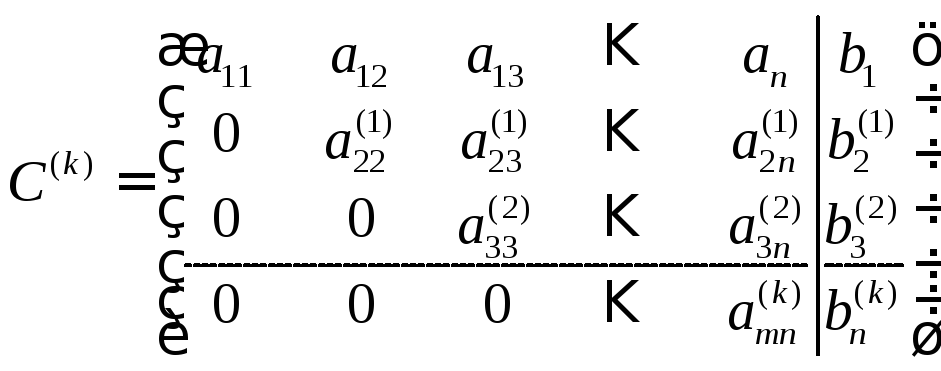
Из этой матрицы легко найдём единственное решение, осущесвляя «обратный ход».
Из последнего уравнения имеем:
![]()
Подставляем значение хn в предыдущее уравнение и находим хn-1 и т.д.
![]()
Примеры решения задач.
Задача 1. Найдите сумму матриц:
 и
и 
Решение:
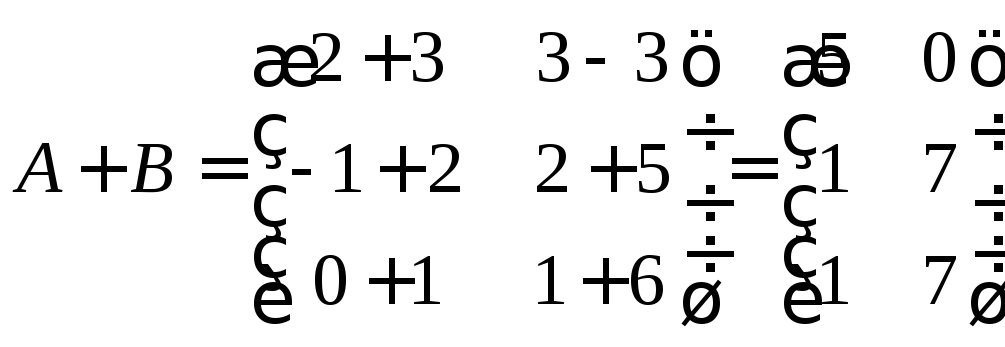
Задача 2. Найдите произведение матриц:
а)
![]()
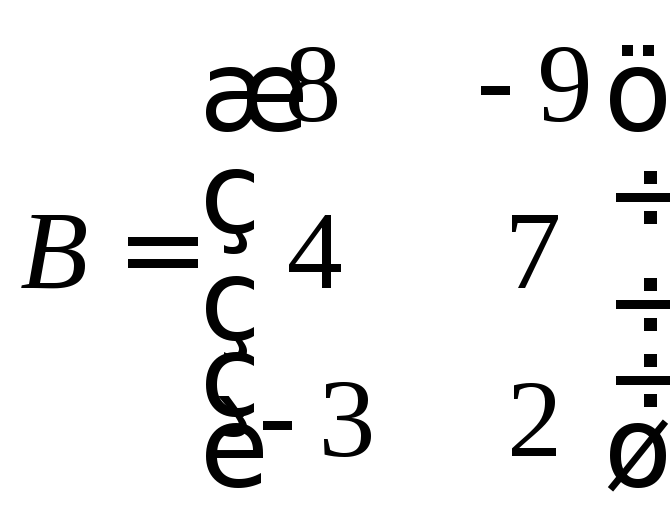
б)
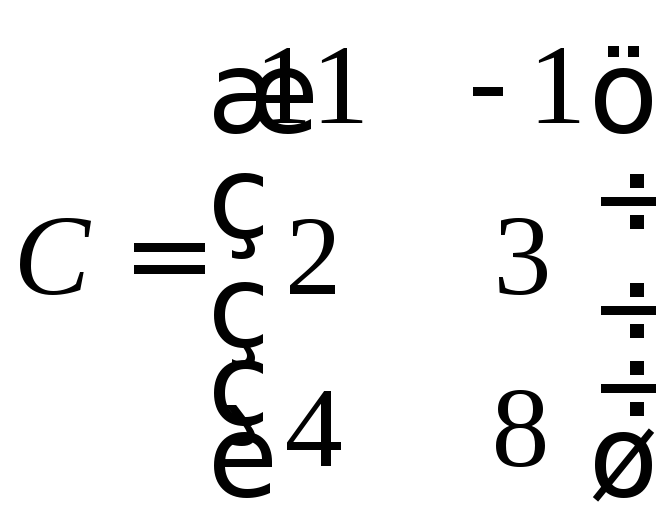
![]()
Решение:
а)![]()

![]() =
=![]()
б)

![]()
Задача
3. Вычислить
определитель второго порядка
![]()
Решение:
![]()
Задача
4. Вычислить
определитель третьего порядка

Решение:
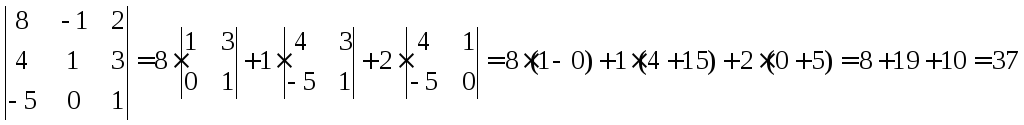
Задача
5.
Найдите обратную матрицу для матрицы
![]()
Решение:
1.Вычислим определитель матрицы
![]() т.е.
матрица невырожденная и ,следовательно,
для нее существует единственная обратная
матрица.
т.е.
матрица невырожденная и ,следовательно,
для нее существует единственная обратная
матрица.
2.Найдем алгебраические дополнения для элементов матрицы:
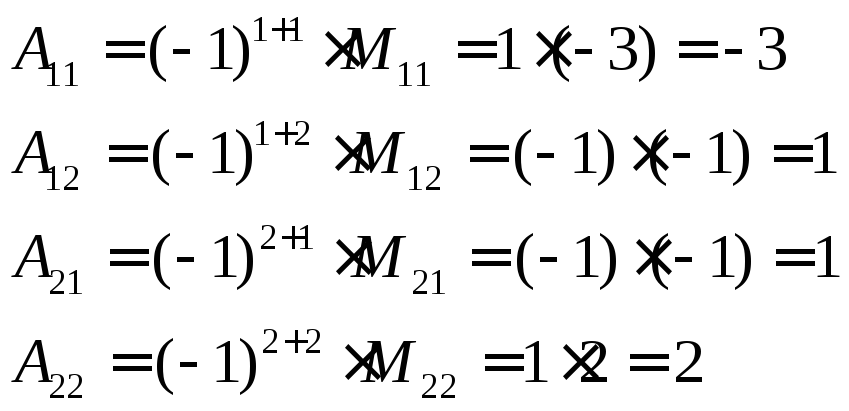
Составим промежуточную матрицу, заменяя элементы матрицы А на соответствующие им алгебраические дополнения:
![]()
3.Протранспонируем
ее:
![]()
4.Найдем
обратную матрицу, умножив А*
на число, равное
![]()
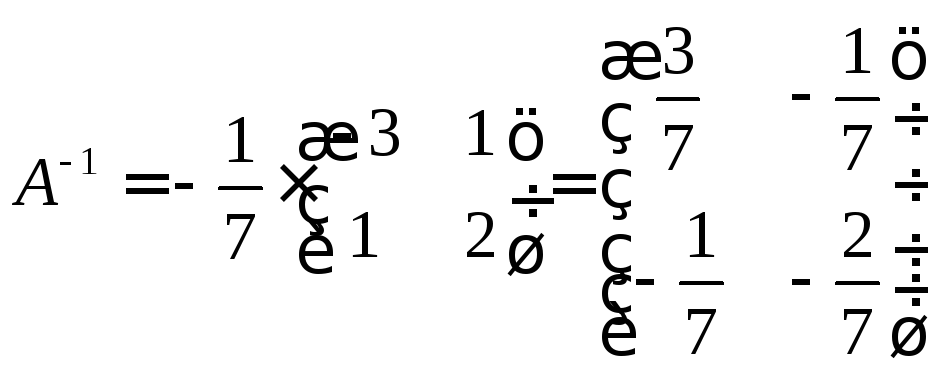
5.Проверкой убедимся, что вычисления выполнены верно:
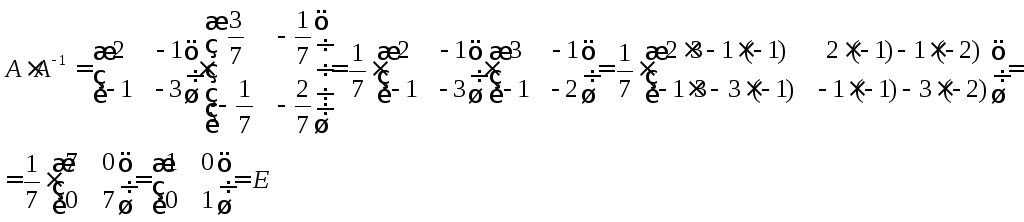
Задача
6. Решите
матричное уравнение
![]() и сделайте проверку решения, если
и сделайте проверку решения, если
![]()
![]()
![]()
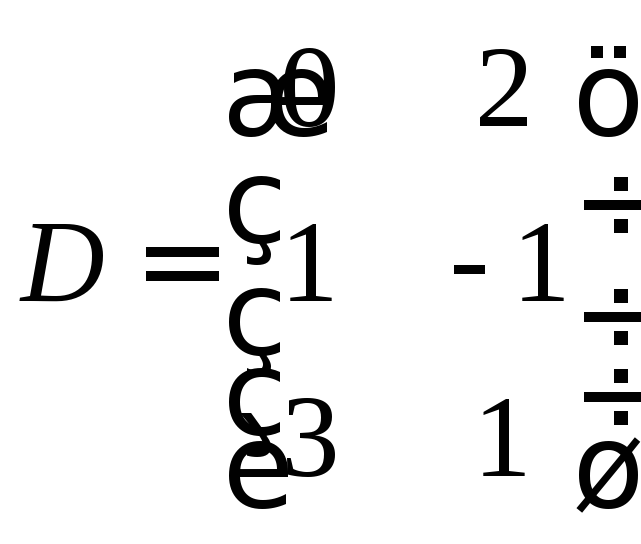
Решение:
1.Вычислим
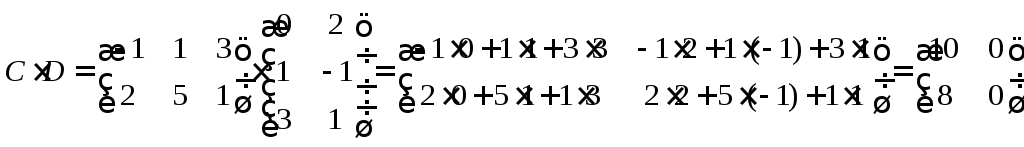
2.
![]()
3.Найдем М-1
а)
![]()
б)
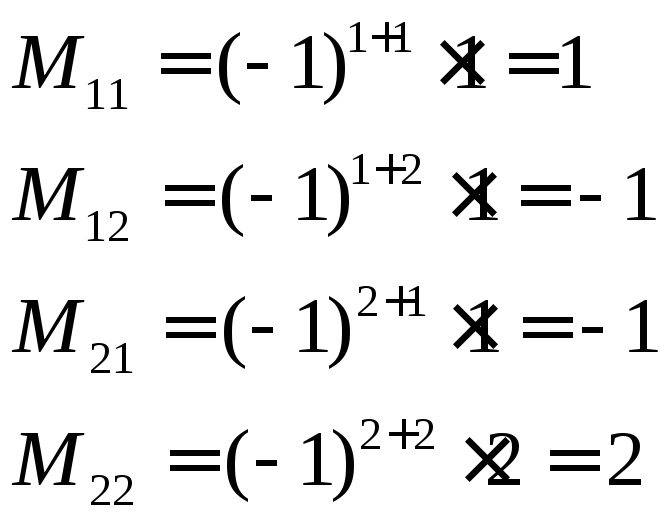
в)
![]()
г)
![]()
д)
Проверка
![]()
![]()
4.Найдем N-1
а)
![]()
б)
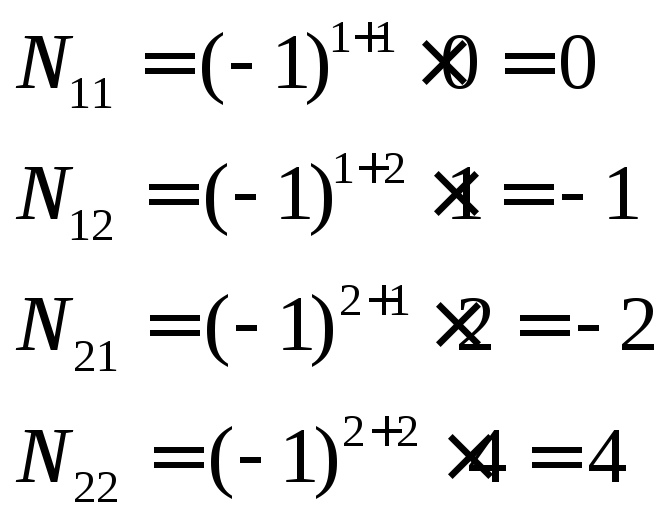
Промежуточная
матрица
![]()
в)
![]()
г)
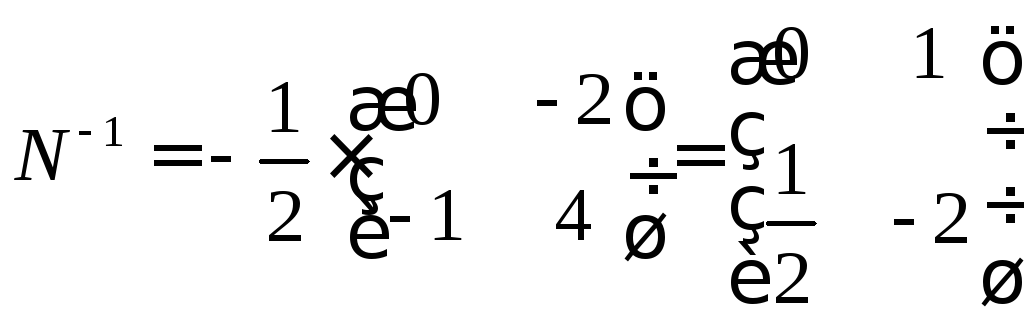
д)
Проверка
![]()

5.
![]()
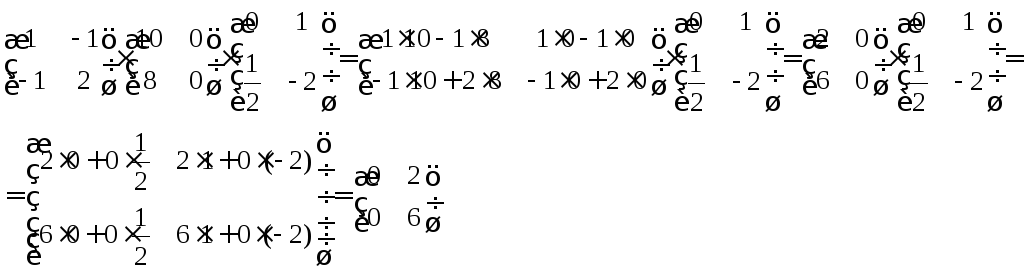
Проверка
правильности решения матричного
уравнения
![]()
![]()
Проверим правильность этого равенства
Получим
 , равенство верно.
, равенство верно.
Ответ:
![]()
Задача 7. Решите систему уравнений по правилу Крамера
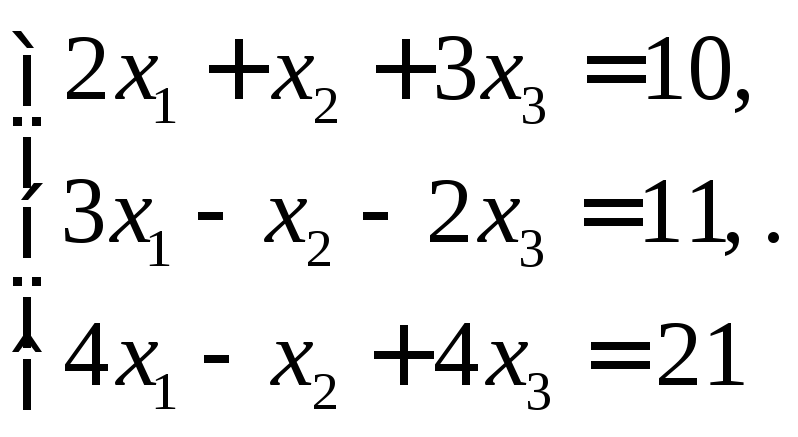
Решение:
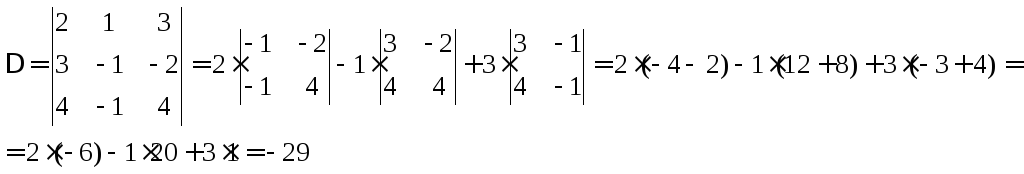
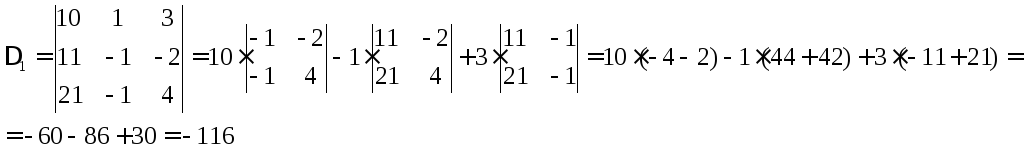
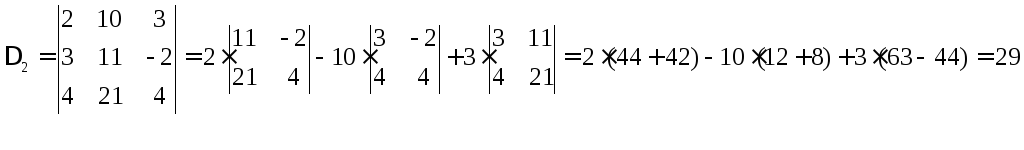
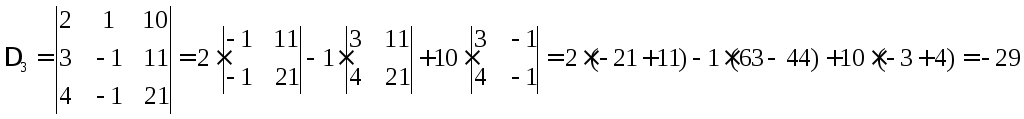
![]()
![]()
![]()
Проверка:

Ответ: (4;-1;-1)
Задача 7. Решите систему уравнений
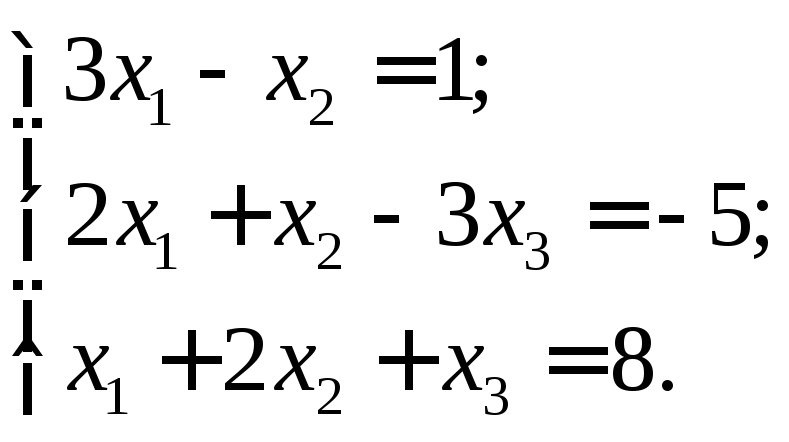
матричным методом (методом обратной матрицы).
Решение:
1.Запишем систему в виде матричного уравнения
 ;
;
![]()
2.Найдем
матрицу, обратную матрице
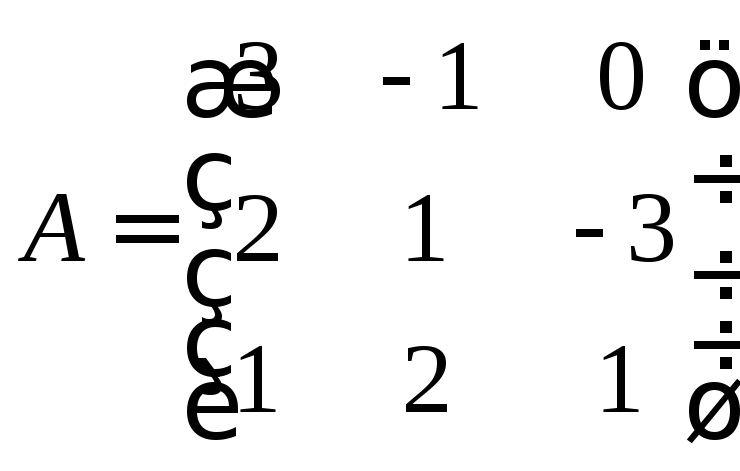 ;
;
а)
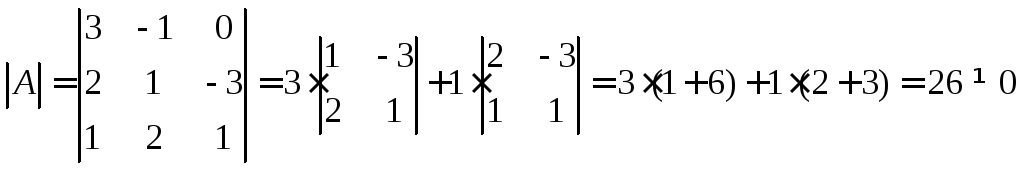
б)
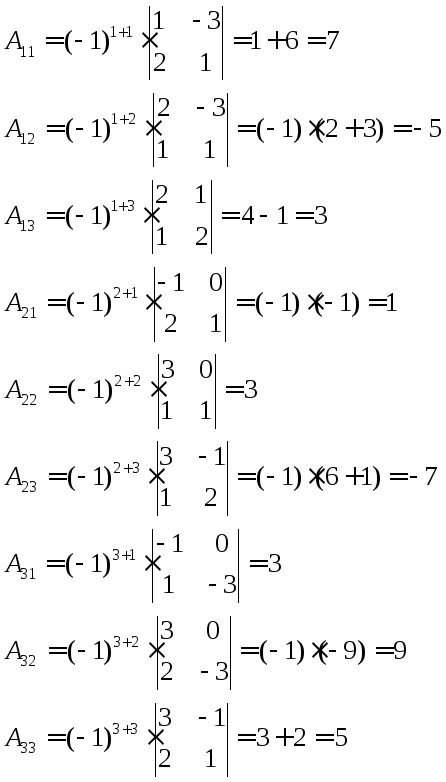
Промежуточная
матрица имеет вид

в)
Транспонируем ее и получаем
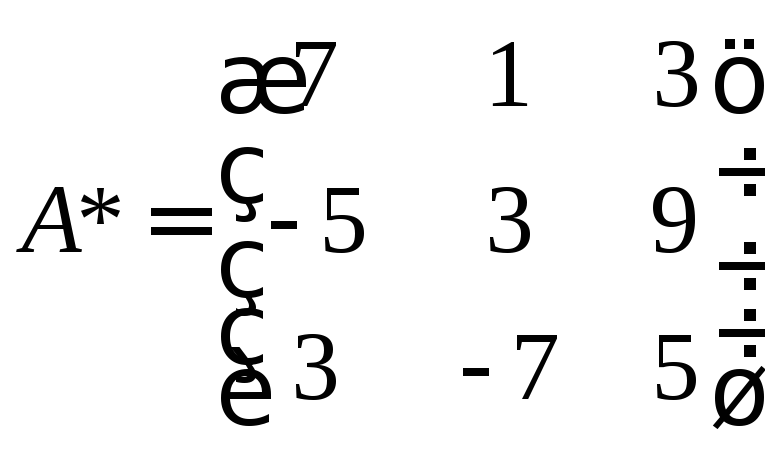
г)
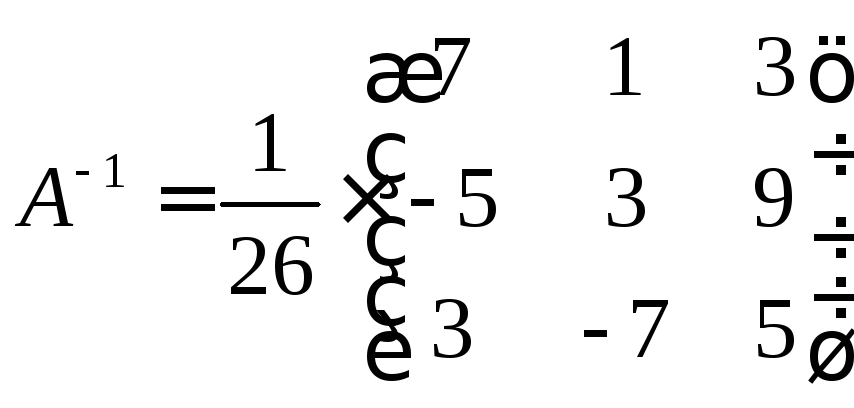
3.
![]()

Проверка:

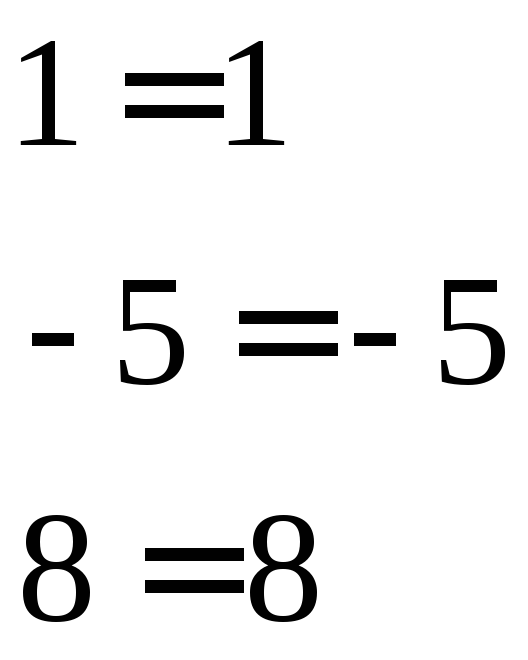
Ответ: (1;2;3)
Задача 9. Решите методом Гаусса систему линейных уравнений и сделайте проверку решения
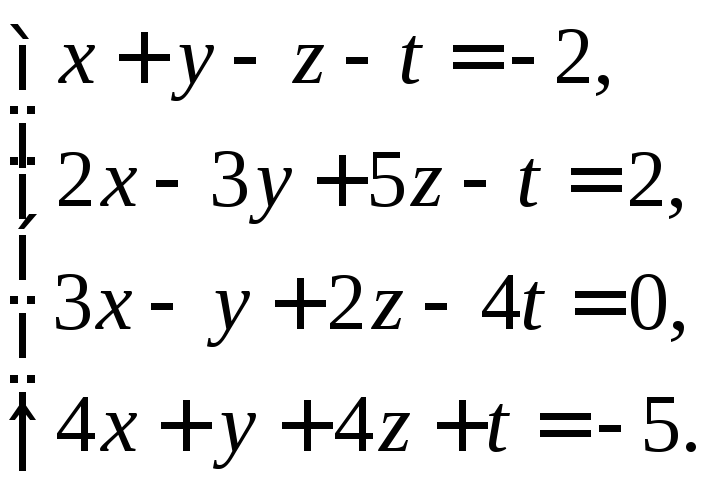
Решение:
Составим расширенную матрицу и выполним преобразования:




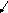

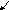
Имеем соответствующую нашей матрице систему линейных уравнений:
 x+
y -z -t=-2,
x+
y -z -t=-2,
-5y+7z+t=6,
z+3t=-2,
-35t=35
1) -35t=35; t=-1
2) z-3=-2; z=1
3) -5y+7-1=6; y=0
4) x-1+1=-2; x=-2
Проверка:
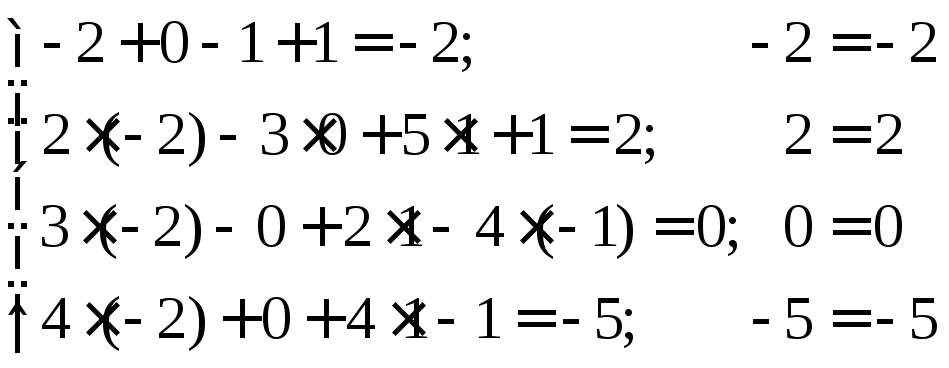
Система
решена верно.![]()
Ответ: (-2; 0; 1; -1)
