Будем иметь:

JIσ = 0 , JIIσ = −3τ2 , J IIIσ = 2τ3 .

Уравнение, определяющее главные нормальные напряжения, принимает вид:

σ3 −3τ2σ−2τ3 = 0 .

Легко видеть, что значение σ = 0 корнем уравнения не является, и напряженное состояние – трехосное.

Определяя подбором один корень σгл1 = −τ , приведем кубическое уравнение к квадратному, которое будет иметь вид:

σгл2 −3τσгл −2τ2 = 0 .

Решение этого уравнения позволяет получить еще два корня:

σгл2 = 2τ , σгл3 = −τ .

Окончательно, для главных нормальных напряжений можем записать:

σ1 = 2τ , σ2 = σ3 = −τ .

3. Закон сплошности. Теория деформаций

3.1. Деформированное состояние в точке. Зависимости Коши

Под деформированием (деформацией) сплошного тела будем понимать процесс изменения положений точек тела, при котором изменяются взаимные расстояния между ними.

Из определения следует, что деформирование тела обусловлено взаимными перемещениями точек. Поэтому характеристики деформирования (деформации), в конечном счете, представляются через эти перемещения.

Под перемещением точки будем понимать вектор, имеющий своим началом исходное положение точки, а концом − положение, в которое точка приходит после деформации.

46

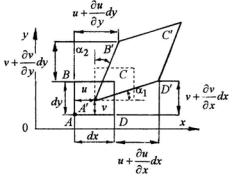
Проекции полного перемещения точки на координатные оси x , y , z обозначим через u , v , w .

Рассмотрим элемент тела в форме прямоугольного параллелепипеда, положение которого определяется точкой A , имеющей координаты x , y , z . Грани параллелепипеда параллельны коор-

динатным плоскостям, а ребра равны соответственно dx , dy , dz .

Будем решать поставленный вопрос о взаимосвязи между перемещениями и деформациями для каждой грани параллелепипеда в отдельности. В частности, рассмотрим грань параллелепипеда, лежащую в плоскости xy (рис. 3.1).

Для упрощения предположим, что деформация этой грани будет плоской, т.е. такой, при которой все точки, находящиеся первоначально в одной плоскости, остаются после деформации в той же плоскости. В этом случае w = 0 , a перемеще-

С геометрической точки зрения можно ввести в рассмотрение два типа деформации: изменение длины первоначально прямого отрезка и изменение величины прямого угла. В соответствии с этим в дальнейшем будем различать продольную (линейную) деформацию ε и деформацию сдвига (угловую деформацию) γ .

Продольная деформация определяется как отношение изменения длины элементарного отрезка к его первоначальной длине. Индекс продольной (или линейной) деформации отрезка будем определять тем направлением, которое имел отрезок до деформации. Деформацию сдвига определим как изменение величины первоначально прямого угла. Очевидно, что деформация сдвига должна иметь два индекса (по направлениям двух отрезков, образующих первоначально прямой угол).

47

Определим продольную деформацию отрезка AD , параллельного оси x , длина которого до деформации равна d x .

После деформации точка A переходит в точку A′. Составляющие этого перемещения обозначим через u и v . Компоненты перемещения u и v есть непрерывные функции координат, поэтому мы вправе записать составляющие перемещения точки D в положение D′ в виде величин u + (∂u / ∂x)dx и v + (∂v / ∂x)dx . Посколь-

ку исследуемый отрезок AD первоначально параллелен оси x , его продольную деформацию можем записать в виде:

Чтобы не иметь дело с корнями, перепишем исходное выражение для деформации εx в виде

48

Приравнивая друг другу два последних соотношения, получаем уравнение, определяющее продольную деформацию εx :

Полученное соотношение допускает его линеаризацию и переход к геометрически линейной теории упругости. Действительно, принимая, что деформации и производные от перемещений малы, будем пренебрегать квадратами и произведениями этих величин по сравнению с самими величинами. Отбрасывая эти слагаемые второго порядка малости в полученном соотношении, находим, что

Аналогичные рассуждения относительно длины отрезка A′B′ позволяют получить, что

и вычислить продольную деформацию εy :

Для того, чтобы определить деформацию сдвига, рассмотрим искажение первоначально прямого угла DAB (см. рис. 3.1). В на-

49

шем случае этот прямой угол составлен отрезками, параллельными осям x и y . Будем иметь:

γxy = α1 + α2 .

Принятое допущение о малости деформаций дает нам возможность определить углы α1 и α2 по их тангенсам и получить для

Очевидно, что если повторить подобные рассмотрения для других граней прямоугольного параллелепипеда, можно получить компоненты деформации для трехмерной задачи:

Непосредственно из физического смысла деформаций сдвига можно утверждать, что

γxy = γyx , γyz = γzy , γzx = γxz .

Представления компонентов деформации через перемещения носят название зависимостей Коши.

Знаки деформаций будем определять следующим образом:

-деформация сдвига считается положительной, если происходит уменьшение первоначально прямого угла, и отрицательной, если этот угол увеличивается;

-линейная (продольная) деформация считается положительной, если происходит удлинение элемента, и отрицательной, если элемент укорачивается.

50

Полученные шесть компонентов деформации определяют так называемую «чистую» деформацию элемента. Такое определение введено, поскольку в общем случае при деформировании тела для его отдельного элемента возможны следующие варианты:

-поступательное перемещение элемента как целого;

-вращательное перемещение (поворот) элемента как целого;

-«чистая» деформация элемента.

Рассмотрим, что представляют собой первые два вида поведения элемента и выясним, можно ли их охарактеризовать через известные (заданные) функции перемещений u , v и w .

Чтобы определить поступательное движение (перемещение) ка- кого-либо элемента тела как целого, достаточно задать перемещение одной его точки. У нас есть точка с заданными перемещениями – точка А. Значит компонентами поступательного перемещения элемента как целого будут значения u , v и w в точке А и, таким образом, дополнительных характеристик для определения этого вида перемещения элемента тела не требуется.

Поворот элементарного параллелепипеда в целом будем определять проекциями угла поворота его главной диагонали на координатные плоскости. Эти проекции равны углам поворота граней параллелепипеда в своих плоскостях, обозначаются как ωx , ωy ,

ωz и носят название компонентов элементарного вращения.

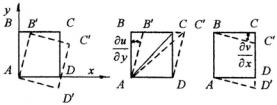
Представим компоненты элементарного вращения через производные от перемещений u , v и w . Рассмотрим поворот одной грани – грани, лежащей в плоскости xy (рис. 3.2).

Поворот осуществляется вокруг оси z , значит, это будет компонент элементарного вращения ωz . Угол поворота грани опреде-

51