рассматриваемого элемента конструкции; - выбор критериев прочности и/или жесткости и оценка работо-

способности элемента конструкции.

Приведенная общая схема решения задачи прочности и жесткости для любого элемента конструкции определяет и место каждой дисциплины в рамках механики деформируемого твердого тела, и взаимосвязь между ними. Например, если наделить модель тела только свойством упругости, можно построить аппарат теории упругости. Аналогично строится аппарат теории пластичности или теории ползучести. Очевидно, что для этих трех дисциплин реализация законов равновесия и сплошности приводит к одним и тем же уравнениям; сохраняются и все понятия напряженного и деформированного состояний. Отличаться же построенные математические аппараты будут только уравнениями механического состояния, которые в каждом случае нужно получать отдельно. Решение, например, упруго-пластической задачи требует совместного применения аппаратов теории упругости и пластичности и стыковки полученных решений.

2. Закон равновесия. Теория напряжений

2.1. Напряженное состояние в точке

Прежде чем приступать к описанию равновесия бесконечно малой частицы (элемента объема) тела, нужно установить, для каких сил эти уравнения будут составляться, т.е. нам нужно знать, как охарактеризовать (какими неизвестными величинами) напряженное состояние этой частицы.

В механике сплошных сред различают силы двоякого рода:

-объемные силы, относимые к элементам объема (или массы) тела;

-поверхностные силы, действующие на элементы площади, которые можно выделить внутри тела или на его поверхности.

Принимается, что объемная сила, действующая на бесконечно малый элемент объема dV , имеет вид ΦdV , где Φ − некоторый

16

конечный вектор, Φ − сила на единицу объема. Компоненты объемных сил, отнесенные к прямоугольным координатным осям, обычно обозначают через X , Y , Z .

Для поверхностных сил принимается, что сила, действующая на бесконечно малый элемент поверхности (бесконечно малую элементарную площадку) dF , имеет вид prn dF , где pn − некоторый

конечный вектор. Величина pn − усилие, отнесенное к единице

площади, или полное напряжение на площадке. Полные напряжения в пределах элементарной площадки можно считать постоянными.

Очевидно, что величина силы pn зависит от ориентировки эле-

ментарной площадки в теле, которую можно охарактеризовать направлением внешней нормали n . Компоненты поверхностной силы pn , отнесенные к прямоугольным координатным осям, обычно

обозначают как X n , Yn , Zn .

Полное напряжение, действующее на координатной площадке с нормалью x , можно разложить на две составлявшие:

-нормальную составляющую σ, перпендикулярную к плоскости сечения;

-касательную составляющую τ , лежащую в плоскости сечения,

которую можно еще раз разложить по направлениям координатных осей y, z .

Для обозначения нормальной составляющей (нормального напряжения) достаточно одного индекса, определяющего рассматриваемую площадку (индекс площадки – индекс ее внешней нормали). В данном случае имеем нормальное напряжение σx (рис. 2.1).

Знаки напряжений на координатных площадках принимаются

17

согласно следующим правилам. Нормальное напряжение будем считать положительным, если оно является растягивающим (если его направление совпадает с направлением внешней нормали к площадке). Для касательных напряжений правило знаков вводится следующим образом: если нормаль к площадке совпадает с положительным направлением координатной оси, то положительные касательные напряжения будут направлены по положительным направлениям двух других координатных осей. На рис. 2.1 показаны положительные направления напряжений.

Через данную точку тела можно провести бесконечное множество площадок. Напряженное состояние в точке определим как совокупность напряжений, действующих на всех элементарных площадках, проходящих через рассматриваемую точку. Но хотя площадок, проходящих через данную точку, бесчисленное множество, нам не придется искать бесконечное множество неизвестных напряжений на них. Можно доказать, что

напряжение на произвольной площадке в точке тела определяется через составляющие полных напряжений, действующих на трех взаимно перпендикулярных площадках, проходящих через эту же точку.

Проведем через точку тела три координатные плоскости xy , yz ,

zx и четвертую плоскость с внешней нормалью n на бесконечно малом расстоянии h от рассматриваемой точки. Указанные плоскости определяют тетраэдр, показанный на рис. 2.2.

Проведя разложение полных напряжений на трех координатных площадках, мы получим девять составляющих этих напряжений.

Рассмотрим равновесие тетраэдра. Условие равенства нулю суммы проекций всех сил на координатную ось x будет иметь вид:

18

X n dF − σx dF cos (x, n)− τyx dF cos (y, n)− τzx dF cos (z, n)= 0

или

X n = σxl + τyx m + τzx n ,

где dF − площадь наклонной площадки тетраэдра; cos (x, n)= l , cos (y, n)= m , cos (z, n)= n − направляющие косинусы нормали n .

Еще два условия равновесия ∑Y = 0 и ∑Z = 0 позволяют получить:

Yn = τxyl + σy m + τzy n ,

Zn = τxzl + τyz m + σz n .

Таким образом, составляющие полного напряжения на любой элементарной площадке в данной точке определяются через девять составляющих полных напряжений на координатных площадках, проходящих через эту же точку. Совокупность этих девяти напряжений будем называть тензором напряжений, а сами напряжения − компонентами тензора напряжений:

Отметим, что тензором может быть не всякая совокупность элементов. Компоненты тензора должны обладать вполне определенными свойствами, которые мы будем рассматривать позже.

2.2. Дифференциальные уравнения равновесия элемента сплошного твердого тела

Рассмотрим бесконечно малый объем тела в форме прямоугольного параллелепипеда с размерами ребер dx , dy , dz . Начало ко-

19

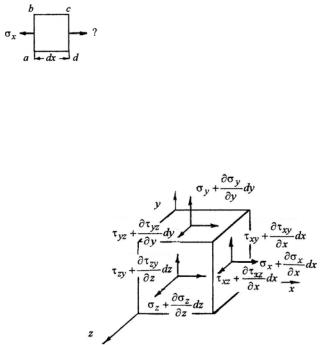
ординат определяет вершину и положение параллелепипеда. Компоненты напряжений на трех координатных площадках, проходящих через начало координат, известны: σx , σy , τxy и т.д. Для

описания равновесия параллелепипеда необходимо знать, какие напряжения действуют на его остальных трех площадках.

Для простоты рассмотрим параллелепипед с напряжением σx , действующим на грани ab

(рис. 2.3). Так как ребро dx определяет бесконечно малый линейный элемент, то напряжение на грани cd можно представить как сумму

напряжения σx и малого приращения этого напряжения на отрезке от ab до cd : σx + (∂σx / ∂x)dx . Рассуждая аналогичным образом,

можно найти все напряжения на оставшихся трех гранях параллелепипеда (рис. 2.4).

Рис. 2.4

Для параллелепипеда, как для пространственно нагруженного тела, должны записать шесть условий равновесия. Из условия равновесия ∑ X = 0 (уравнения сил) следует:

20

Здесь X − компонента объемной силы. После некоторых преобразований уравнение приводится к виду:

Записывая аналогичным образом условия ∑Y = 0 и ∑Z = 0 , можем получить еще два уравнения:

∑M z = 0 начало координат целесообразно поместить в центре

элементарного параллелепипеда. В этом случае из уравнений выпадут слагаемые, определяемые объемными силами и нормальными напряжениями. Условие ∑M x = 0 позволяет получить следую-

щее уравнение:

После приведения подобных членов и отбрасывания бесконечно малых второго порядка получаем, что τyz = τzy . Из условий

∑M y = 0 , ∑M z = 0 аналогичным образом находим, что τzx = τxz

и τxy = τyx .

21