
Шпоры по автоматике
.docШпаргалки по куру «Теория автоматического управления, часть 1»
Соответствует курсу, читаемому в Национальный Исследовательский Ядерный Университет (Московский Инженерно-Физический Институт) на факультете Автоматики и электроники на шестом семестре. Лектор Шапкарин А.В.
Варианты печати:
-
страницы 2-13 (без индекса)
-
страницы 2-14 (с индексом)
15-я страница пустая, печатать смысла нет.
Печатать на листах с одной стороны, потом разрезать.
Во время сдачи экзамена обычно разрешено пользоваться собственноручно изготовленной таблицей динамических звеньев. В билет входит 2 теоретических вопроса и одна задача. Задачи типов разных, лектор на консультации пояснит.
Copyright (C) 2009 Balconman, Leya89, Lisa, mata, Nast, salimr, ssvda, technoboy, zHz, Кукурузо, Тэра.
Permission is granted to copy, distribute and/or modify this document
under the terms of the GNU Free Documentation License, Version 1.3
or any later version published by the Free Software Foundation;
with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
A copy of the license is included in file LICENSE.TXT or can be found at http://www.gnu.org/licenses/fdl.html.
|
1. Понятия САУ и САР. Функц схемы САР. Автоматическое управление – осуществление некоторых операций без непосредственного участия человека, направленных на поддержание или улучшения работы объектов управления. Автоматич. Регулирование – поддержание регулярной величины на заданном постоянном значении или изменении её по заданному закону без непосредственного участия человека. А.Р. – частный случай А.У. Функциональная схема САР:
У — устройство управления И — исполнительное устройство ОР — объект регулирования ИУ — исполнительное устройство |
2. Классификация автоматических систем. 1) по принципу действия - Система разомкнутого цикла(без утр. управл-я) - Замкнутые системы(есть инструмент сравнения и усилитель) - Системы комбинированного управления 2) По виду входного управл сигнала g(t) - g(t) = const – система стабилизации - g(t) = f(t) - система программного регулиров - g(t) = неизвестная функция – следящая система. 3) по виду сигналов действия в системе. - непрерывные - дискретно непрерывные -импульсные 4) По виду мат описания.
|
3. Построение линейной модели следящей системы. x’(t) = F(x(t) , u(t)) , где x(t) –вектор состояния системы, u(t) - вектор входных воздействий. …. x’n(t) = fn(x1,…,xn , u1,…,um)
Вектор выхода системы: y(t) = G(x1,…,xn , u1,…,um) G – нелинейная функция. Линеаризация: x1 = x0 + Δx1 , x0 – нулевое решение.
Система принимает вид линеариз. ур-ия во временной области: y(t) = Cx(t) + Du(t), где: ┌ ∂f1/∂x1…….∂f1/∂xn ┐ A = │ ……………….│ - матрица системы └ ∂fn/∂x1……∂fn/∂xn ┘ ┌ ∂f1/∂u1 ….. ∂f1/∂um ┐ B =│ … │ - матрица управления └ ∂fn/∂u1 ….. ∂fn/∂um ┘ ┌ ∂g1/∂x1… ... ∂g1/∂xn ┐ С =│ … │ - матрица наблюдения └ ∂gr/∂x1……∂gr/∂xn ┘ ┌ ∂g1/∂um…... ∂g1/∂um ┐ D = │ … │ - матрица прямой └ ∂gr/∂um……∂gr/∂um ┘ передачи. |
|
|
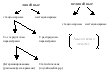
4. Элементы структурных математических моделей систем 1) Линия связи → направления передачи сигнала 2)
Узел
3
K
Показывает сигнал поступает на неск. входов
4 F
y(t)=F(u(t))
5 1/S
y(t)= ∫ u(t) dt + y0; 0 y(s)/ u(s) = 1/s 6
V 7
X
8) нелинейные операции:
Y = U(t) * V(t) V |
5. Опис. линейных систем в пространстве переменных состоян. X(t) — вектор состояния x´(t) = F(x(t),u(t)) – описание в форме Коши. u(t) — вектор воздействий на систему.
x1´(t) = f1(x1,…,xn, u1…um) форма Коши xn´(t) = fn(x1,…,xn, u1…um) min переменных способом. Которых можно описать процессы => кол-во переменных определяют размерность в-ра состояний Линеаризации происходит относительно стационарной точки(положения равновесия) – эта точка является опорной в n-мерном прост-ве. Необходимо иметь сист. Ур-ий для выхода: yi(t)=Gi(x1…xn, u1…um) Пусть система имеет равновесие в 0. x0=0; x1=x0+Δx1 => x1= Δx1 Линейная система приобретет вид: y(t) = Cx(t) + Du(t) система df/dx1…. df1/dxn матрица системы A = . . . . . производная вы- _ dfn/dxn . .dfn/dxn_ числяется в 0 [n*n]
B- матрица управления [n*m] (dF/du) С- наблюд.;Связ. c датчиками [r*n] (dGr/dxn) D- матр. прям. передю сигнала [r*m] (dGr/dum) При D=0 (часто) скачок на входе на вых. Передаваться не будет. См. также вопрос 3. |
6. Способ составления CММ по ДУ в форме Коши. Um Y
Y(t) = Cx(t) + Du(t) (2) sx(s) = Ax(s) + Bu(s) x(s) = Bu/(s-A)
|
|
|
7. (1/2) Правила преобразования СММ 1) Последовательное соединение динамич. звенье W(s) = w1(s)*w2(s)*w3(s)
2) Параллельное соединение n W(s) = ∑ wi(s) i=1
3) Соединение с обр. связью ε = u-v y = ε *w1(s) v = y*w2(s) Ф(s) = w1(s) / (1-w1(s)*w2(s)) – передаточ ф-ия замкнутой системы ПОС: Ф(s) = w1(s) / (1-w1(s)*w2(s))
4) Перенос узла с выхода Эл-та на вход
5) перенос узла со входа на выход.
|
7. (2/2) Правила преобразования СММ 6)Перенос сумматора со входа на выход
7) Перенос сумматора с выхода на вход
8)Перестановка элементов суммирования
9) Перегруппировка элементов суммирования
|
8. Определение передаточной функции. Вычисление матричной передаточной функции системы. Система линеаризованных уравнений записана во врменной области => для нее существует передаточная функция (для стац. Системы). Для нестационарных случаев перед. Функц. Не пользуются. Аппарат передаточной ф-ии требует нулевых начальных условий по координат. Вектора состояния. Аппарат перех-х функции вводится при переводе системы из временной обл-ти в комплексную с пом. Преобразований Лапласа. +∞ L{xi(t)} = xi(s) = ∫xi(t)* e^(-st) dt 0 s- переменная Лапласа p- оператор дифференцирования p = d/dt
u(t) => u(s) y(t) => y(s) L{d/dt , xi(t)} = s* xi(s) – xi(0). xi(o)=0
Sx(s) = Ax(s) + Bu(s) Y(s) = Cx(s) + Du(s)
[SE – A]x(s) = Bu(s) X(s) = Bu(s) / [SE – A] Y(s) = [C[SE – A]‾¹B +D]u(s) - передаточная функция.
Матричная передаточная функция W(s) W11(s)…. W1n(s) для линеар-ойначальной W(s)= . . . . . системы с нулевыми _ Wr1(s) Wrn(s) _ условиями
Wij = yi(s) / uj(s) – отношение i-го входа j-ому выходу. W(s) = C* (adj[SE-A] / det[SEiA]) *B –D При D=0 скачков на выходе нет. Нет прямой передачи. Wij(s) A: n*n det[SE – A] – полином n-ого порядка. Для любого Wij(s) имеет в знаменателе полином n-ого порядка.
Wij(s) = (b0sn-1+b1sn-1+…+bn-1) / (sn+a1sn-1+…+an-1s+an) – дробн. Рацион. Функция. Когда нет прямой передачи порядок полинома в числителе строго меньше в знаменателе.
При D≠0 W(s) = s – дифф. Физически не реализуемо.
|
|
|
9. Правила преобразования основных типов динамических звеньев. См. вопрос №7.Вместо W писать G. Cв-ва7,8,9 не надо
|
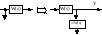
10. Метод привидения к диагональной форме. W(s) = y(s) / u(s) = (b0sn+b1sn-1+…+bn) / (sn+a1sn-1+…+an) = =M(s) / D(s) ; a0=1 Пусть известны корни знаменателя. n n D(s) = ∏(s – λi) λi – корни; W(s) = ∑(Ci / (s – λi)) + C0 = i=1 i=1 y(s)/u(s) Ci – вычеты W(s) вычисление в полюсах W(s). Корни в знаменателя –полюсы. Корни полинома в числителе–нули W(s). Сi = lim(s – λi)W(s) = lim M(s) / [(d/ds)D(s)] s →λi s →λi C0 – целая часть передаточной функции C0 = limW(s) = b0 s→∞ В качестве в-ра состояния: xi(s) = u(s)/ (s – λi) y(s) = ∑cixi(s) + c0u(s); y(t) = ∑cixi(t) + c0u(t); sxi(s) = λixi + u(s); по обратному преобр-ию Лапласа: =>
x’2 = λ2x2 + u A = Λ = │ 0 λ2 . . . . 0 │ B= │ ..│ …… │ 0 . . . . . . │ └ 1┘ x’n = λnxn + u └ 0 …. .. λn ┘ C = [C1 ... Cn] ; D= C0
|
11. (1/2)Составление ур-ний состояния по передат-ной ф-ции методом разложения на простые множ-ли. Необходимо знать корни полиномов числ-ля и знамен-ля:
Для
удобства моделирования рассм. отдельную
ячейку i
|
|
|
11. (2/2)Составление ур-ний состояния по передат-ной ф-ции методом разложения на простые множ-ли. ПОС позволяет легко исследовать сис-му частотными методами Система ур-ний:
|
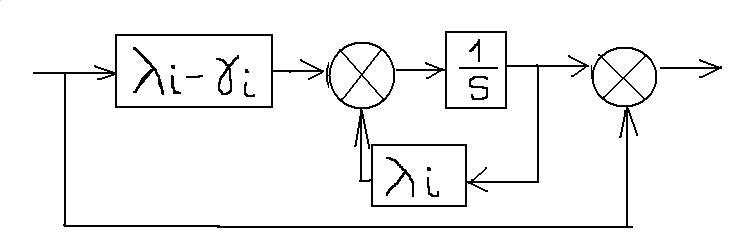
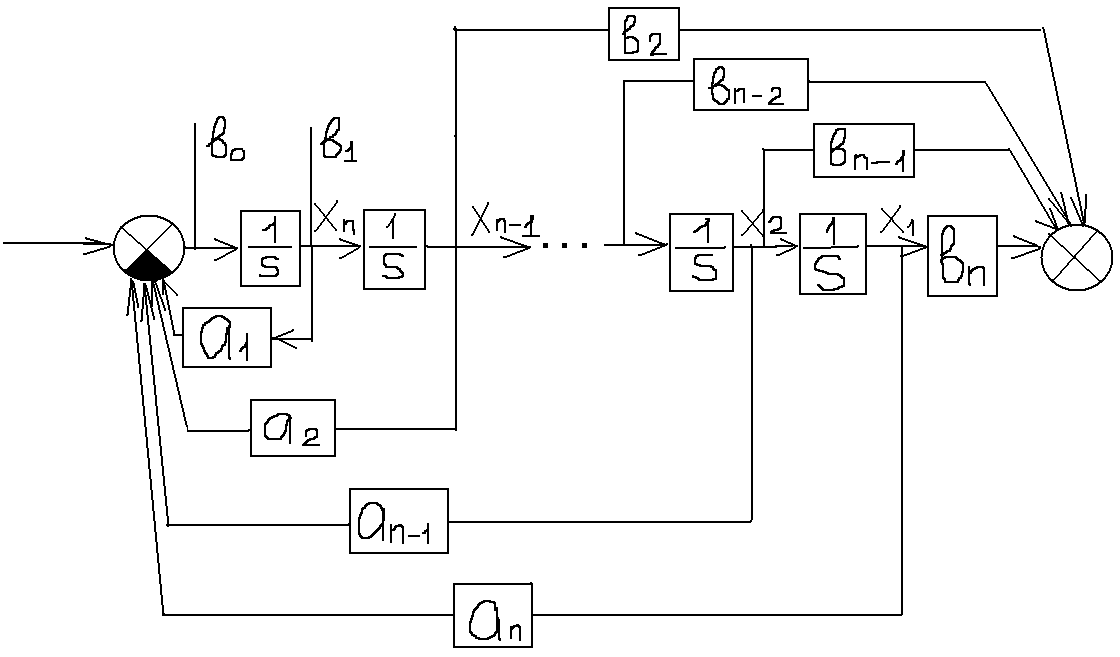
12. (1/2) Составление ур-ний состояния по перед. ф-ции методом, применяемым при аналоговом моделировании. Пусть
Расписываем M(s):
Послед-но n штук интеграторов |
12. (2/2) Составление ур-ний состояния по перед. ф-ции методом, применяемым при аналоговом моделировании.
Не надо искать корни, не нужны предварительные расчеты
|
|
|
13. Составление ур-ний состояния передаточной ф-ции методом привед-я к канонич-кой форме.
Вводим вектор состояния => получим из ур-ния n-го порядка ур-ния n-1 порядка
(!)
|
14. Понятие переходной и импульсной переходной характеристик, способы нахождения их аналитических выраженй. Переходная хар-ка – реакция системы на входное воздействие, представленная как ф-ция времени. Перех. хар-ка – реакция системы на единичную ступеньку.
Импульсная
хар-ка – реакция сист. на абстрактный
импульс
приближение ф-ции к δ(t)
Если
есть
(*)-если пор-ки передат. ф-цией не равны. Если
порядки =, то при разбиении на дроби
появится целая часть
Выходной
сигнал можно вычислять как интеграл
свертки во временной области:
y(t) – свертка сходного сигнала с ИПХ. |
15. Амплитудная и фазовая частотные характеристики элемента. Их мат. и физ-кая интерпретация. Частотной
хар-кой ТДЗ наз. ф-цию комплексного
аргумента jω
полученную путём формальной замены
W(s)
s=
jω
Преобразование Фурье (частотные спектры сигналов) показывает, как распределена по частотам хар-ка системы:
Частотные
хар-ки исслед-ся при подаче гармонич.
входного воздействия
Годограф передат.
ф-ции: (на примере
Длина век-ра – модуль перед. ф-ции H(ωi) Θ(ωi) – сдвиг по фазе
|
|
|
16. Понятие типовых динамических звеньев;минимально и неминимально фазовые ТДЗ. Динамическое звено — математическая модель элемента или его части, записанная в виде диф.ура или передаточной ф-ции. Динамические звенья, которые описываются диф.урами не выше 2-го порядка,принято называть Типовыми динамическими звеньями.Передаточная функция называется минимально-фазовой,если все её нули расположены в левой половине S плоскости . ТДЗ W(s)=K усилительное (безынерционное) звено W(s)=KS идеальное диф-щее звено W(s)=K/S идеальное интегр-щее W(s)=K/TS+1 апер. 1го.пор-кa W(s)= W(s)= W(s)=TS+1 диф звено 1 порядка W(s)= W(s)= W(s)=
|
17. (1/2) Годограф и логарифмические амплитудные и фазовые хар-ки апериодического уст звена.
=
Избавимся
от
амплитудно-фазовая
частот хар-ка для
|
17. (2/2) Годограф и логарифмические амплитудные и фазовые хар-ки апериодического уст звена.
Годограф:
|
|
|
18. (1/2) Годограф и ЛАФЧХ неустойч звена
Годограф:
Избавимся
от
|
18. (2/2) Годограф и ЛАФЧХ неустойч звена
ЛАФЧХ:
|
19. Годограф и ЛАФЧХ итегрируещего звена
|
|
|
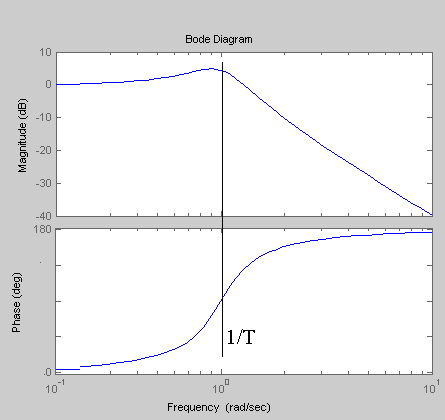
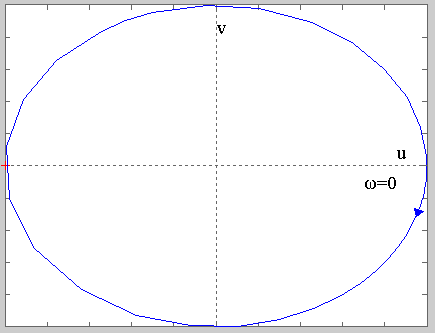
20. Годограф и ЛАФЧХ колебательного устойчивого З.
0< ξ <1 –– коэффициент затухания От Т нет зависимости, только от ξ. W(jω)=1/(1–T2ω2+2ξTj ω)=(1– T2ω2–2 ξTj ω)/((1– T2ω2)2+4 ξ2T 2ω2) u(ω)= (1– T2ω2)/((1– T2ω2)2+4 ξ2T2ω2) v(ω)= –2 ξTj ω/((1– T2ω2)2+4 ξ2T2ω2) H(ω)= Θ(ω)= –arctan(2ξT ω/(1– T2ω2)), 0≤ω≤1/T Θ(ω)= ––arctan(2ξT ω/(1– T2ω2)), ω>1/T Годограф:
ЛАФЧХ:
L(ω)=20lg H(ω) ξ3<ξ2<ξ1; при ξ =1 получаем 2 послед. Апер. Звена (можно сложить 2 характеристики) |
21. Годограф и ЛАФЧХ колебательного неустойчивого звена
0< ξ <1 –– коэффициент затухания От Т нет зависимости, только от ξ. W(jω)=1/(1–T2ω2 –2ξTj ω)=(1– T2ω2+2 ξTj ω)/((1– T2ω2)2+4 ξ2T 2ω2) u(ω)= (1– T2ω2)/((1– T2ω2)2+4 ξ2T2ω2) v(ω)= +2 ξTj ω/((1– T2ω2)2+4 ξ2T2ω2) H(ω)= Θ(ω)= +arctan(2ξT ω/(1– T2ω2)), 0≤ ω≤1/T Θ(ω)= ++arctan(2ξT ω/(1– T2ω2)), ω>1/T Годограф:
ЛАФЧХ:
L(ω)=20lg H(ω) ξ3<ξ2<ξ1 |
22. Годограф и ЛАФЧХ вырожденного колебательного З. ξ=0.
W(jω)=1/(1–T2ω2) u(ω)= 1/(1–T2ω2) v(ω)= 0 H(ω)= Θ(ω)=0, 0≤ ω<1/T Θ(ω)= –, ω>1/T;1/T – полюс функции Годограф:
ЛАФЧХ:
L(ω)=20lg H(ω)
|
|
|
23. Годограф и ЛАФЧХ мин-фазового дифф. З. 1-го пор-ка. W(S)=TS+1. Обратное к апериодическому => графики обратные в лог. масшт. Годограф не переворачивается, т.к. он линейном масшт. W(jω)=1+Tjω u(ω)= 1 v(ω)= Tω H(ω)= Θ(ω)=arctan(Tω) Годограф:
ЛАФЧХ:
|
24. Годограф и ЛАФЧХ немин-фазового дифф. З. 1-го пор-ка. W(S)=TS–1. W(jω)= –1+Tjω u(ω)= –1 v(ω)= Tω при ω=0 W= –1 => Θ=180o при ω=∞ W практически мнима (а мнимая часть положительна) => Θ=90o H(ω)= Θ(ω)= –arctan(Tω) Годограф:
ЛАФЧХ:
|
25. Годограф и ЛАФЧХ идеального дифф. З. 1-го пор-ка. W(S)=S. W(jω)=jω u(ω)= 0 v(ω)= ω H(ω)= Θ(ω)=/2 Годограф:
ЛАФЧХ:
L(ω)=20lg H(ω) |
|
|
26. Годограф и ЛАФЧХ мин-фазового дифф. З. 2-го пор-ка. W(S)=T2S2+2ξTS+1. 0< ξ <1 W(jω)=1–T2ω2+2ξTj ω u(ω)= 1– T2ω2 v(ω)= 2ξTjω H(ω)=
Θ(ω)= arctan(2ξTω/(1– T2ω2)), 0≤ ω≤1/T Θ(ω)= +arctan(2ξTω/(1– T2ω2)), ω>1/T Годограф:
L(ω)=20lg H(ω) ξ3<ξ2<ξ1
|
27. Годограф и ЛАФЧХ немин-фазового дифф. З. 2-го пор-ка. W(S)=T2S2–2ξTS+1. 0< ξ <1 W(jω)=1–T2ω2–2ξTjω u(ω)= 1– T2ω2 v(ω)= –2ξTjω H(ω)=
Θ(ω)= –arctan(2ξTω/(1– T2ω2)), 0≤ ω≤1/T Θ(ω)= ––arctan(2ξTω/(1– T2ω2)), ω>1/T Годограф:
L(ω)=20lg H(ω) |
28. Годограф и ЛАФЧХ вырожденного дифф. З. 2-го пор-ка. W(S)=T2S2+1 (т.е. ξ=0) W(jω)=1–T2ω2 u(ω)= 1–T2ω2 v(ω)= 0 H(ω)= Θ(ω)= 0, 0≤ ω≤1/T Θ(ω)= , ω>1/T Годограф:
ЛАФЧХ:
L(ω)=20lg H(ω) |
|
|
29. Годограф и ЛАФЧХ З. запаздывания W(S)=e–TS W(jω)= e–Tjω u(ω)= cos(Tω) v(ω)= –sin(Tω) H(ω)= Θ(ω)= –Tω Годограф:
ЛАФЧХ:
|
30. Какие преимущества даёт использование логарифмических масштабов при построении частотных характеристик по сравнению с линейными масштабами. ОЛОЛОЛО, короче так: 1) график лог. АЧХ произведения ТДЗ является СУММОЙ лог. АЧХ кадого из них, таким образом, получение лог. АЧХ системы существенно упрощается. 2) асимптотические лог. АЧХ являются прямыми линиями, а не экспонентами, это упрощает их получение и изображение. 3) асимптотические лог. АЧХ имеют фиксированный наклон, кратный 20 дБ на декаду, что эквивалентно 6 дБ/октаву (декада — изменение частоты в 10 раз, октава — в 2 раза) 4) изменения происходят в пределах декады (+- 10 раз) от характерной точки (сопрягающая частота, 1/Т) [а для сложных систем +10 раз от макс. Характерной точки и –10 раз от минимальной] 5) лог. ФЧХ часто бывает симметрична или косо-симметрична относительно сопрягающей частоты (для типовых звеньев) 6) лог. ФЧХ сложной системы является суммой ФЧХ ТДЗ [хотя вроде для лин. Масштаба это точно так же] 7) множество номограмм, шаблонов и приближённых формул составлены именно для лог. масшт. Лог АЧХ: L(ω)=20lg H(ω), где H(ω) — лин. АЧХ. Лог масштаб: на графике расстояния от 0.1 и 1 такое же, как и от 1 до 10 (например). 8) ЛАФЧХ дифф. звена — перевёрнутая ЛАФЧХ соотв. интегрального. |
31. Определение асимптотической устойчивости, устойчивости и неустойчивости мо методу Ляпунова. x` (t)=Ax`(t)+Bu(t) если лин. система [u(t)=0], то x` (t)=Ax(t) Линейная система имеет одно положение равновесия и оно находится в нуле: x` (t)=Ax(t) => Ax(t)=0 => x(t)=0
1) Положение равновесия асимптотически устойчиво, если траектория движения в n-мерном пространстве находится в какой-то точке и стремится к положению равновесия при t→ ∞; 2) Если траектория движения все время находится в некоторой ограниченной области, то такое положение называется устойчивым (траектория не стремится к положению равновесия и не убегает от него); 3) Если траектория, начавшись в некоторой ограниченной области вокруг положения равновесия, удаляется с течением времени от положения равновесия , то данное положение является неустойчивым. |
|
|
32. Прямой метод исследования устойчивости линейных систем. x` (t)= Ax(t) Корни характеристического уравнения: Det [SE-A]=0 → i , i=1…n i – собственные значения матрицы А это знаменатель передаточной функции: Sn+a1S n-1+a 2 S n-2+...+a n=0 1) Условие асимптотической устойчивости: Re i <0 , все корни характер. Уравнения лежат в левой полуплоскости. Если линейная система асимптотически устойчива, то и исходная нелинейная система асимптотически устойчива. 2) Как только найдется хотя бы один Re > 0 , то линеаризованная модель неустойчива, переходная характеристика уходит на бесконечность, исходная нелинейная модель неустойчива. 3) Как только из всех Re i <0 , найдется , лежащая на мнимой оси (один или несколько), возникает неопределенность.
|
33. Алгебраический критерий Гурвица. Метод использования информации о системе в виде характеристического уравнения: Знаменатель W(s) равен 0 => Sn+a1S n-1+a 2 S n-2+...+a n=0 Необходимым условием асимптотической устойчивости является положительность всех коэффициентов. (a i >0 ). Достаточное условие устойчивости (Матрица Гурвица):
a1 a3 а5……..0 1 a2 a4 .........0 Г= 0 a1 a3.........0 0 1 a1.........0 n*n 0...................an
Достаточное условие: положительность всех угловых миноров: a1>0,
|
34. (1/2) Частный критерий устойчивости Михайлова (принцип аргумента) Sn+a1S n-1+a 2 S n-2+...+a n=0 Кор.
Характер. Ур-ия:
Рассмотрим данное выражение как произведение векторов:
Вектора,
проведенные из корней слева поворачиваются
на +,
справа — на –.
Пусть m
коней из n
находятся справа .Приращение аргумента:
argD(jω)= –argD(–jω)
|
|
|
34. (2/2) Частный критерий устойчивости Михайлова (принцип аргумента)
Система устойчива когда нет корней в правой части. (m=0)
Для того, чтобы линейная система была асимптотически устойчива , необх.и достат., чтобы годограф характеристического ур-ия D(jω) начинался на положительной части действительной оси , проходил последовательно n квадрантов в положительном направлении, не попадая в начало координат («проходил» означает, что он должен там побывать, но не обязательно выйти из квадранта)
|
35. (1/2) Критерий устойчивости Найквиста для устойчивых разомкнутых систем. Позволяет исследовать устойчивость замкнутой системы по частотным характеристикам разомкнутой. Основан на критерии Михайлова
↑ Характеристическое уравнение разомкнутой системы:
↑ Характеристическое уравнение замкнутой системы: D(s)=Mp(s)+Dp(s) Разомкнутая система чаще всего устойчива, но есть системы, которые сами по себе неустойчивы. Неустойчивость порождается только неустойчивостью в блоке управления. В большинстве случаев Dp(s) не содержит корней в правой полуплоскости. Когда есть корни в правой полуплоскости система неустойчива. Для устойчивости Dp(s) должна иметь все корни в левой полуплоскости. Введем вспомогательную функцию:
Применяя критерий Михайлова:
|
35. (2/2) Критерий устойчивости Найквиста для устойчивых разомкнутых систем. Пусть объект управления неустойчив. Есть mp штук корней в правой полуплоскости.
1) Разомкнутая система устойчива [mp=0] Замкнутая
система так же устойчива если годограф
разомкнутой системы не охватывает
точку –1 при
2)
Пусть разомкнутая система неустойчива
и имеет
|
|
|
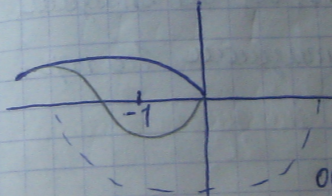
36. Критерий устойчивости Найквиста для неустойчивых разомкнутых систем. Для
системы, неустойчивой в разомкнутом
состоянии, замкнутая система будет
устойчивой, если годограф передаточной
функции разомкнутой системы W(jw)
охватывает точку -1 на комплексной
плоскости в положительном направлении
|
37. Обобщенный критерий устойчивости Найквиста. Для устойчивых замкнутых системы необходимо, что бы она не имела корней в правой полуплоскости. Обобщенный критерий рассматривает случай, когда замкнутая система может быть неустойчивой. Введем: mз – число корней в правой полуплоскости у замкнутой системы. mр – число корней в правой полуплоскости разомкнутой ситсемы Рассмотрим полный диапазон частот
Используя критерий Михайлова:
Если
годограф не делает оборотов вокруг
точки –1 , то система асимптотически
устойчива при
|
38. (1/2) Понятие запасов устойчивости по фазе и модулю.
В
условии эксплуатации параметры системы
по тем или иным причинам могут меняться
в определенных пределах (старение,
температура, колебания и т д) Эти
колебания параметров могу привести
к потере устойчивости системы, если
она работает вблизи границы устойчивости.
Поэтому стремятся спроектировать САУ
так, чтобы она работала вдали от границы
устойчивости, степень этого удаления
называют запасом устойчивости. По
годографу и соответствующим ЛАФЧХ
разомкнутой системы вводится
количественная мера устойчивости в
виде запасов устойчивости по фазе и
модулю. Запас по фазе
входного
и выходного сигналов равны. Запас по
модулю Hm
определяется на частоте
|
|
|
38. (2/2) Понятие запасов устойчивости по фазе и модулю.
Логарифмический запас устойчивости:
С ростом К
увеличивается
|
39. Анализ устойчивости многоконтурных систем.
Процесс исследования на устойчивость начинается с внутреннего контура. Необходимо построить ЛАФЧХ и годограф внутреннего разомкнутого контура. Можно получить 4 результата: Разомкн. внутр. контур Устойчивый: Замкнутый – устойч. или неустойчив. Разомкн. внутр. контур неустойчивый: Замкнутый – устойч. или неустойчив. Wвнутр=W2W3 Предположим получим: Разомкн. Уст => замкн. Вн.контр. неустойч. Годограф переходит точку –1 Тогда необходимо знать, сколько получится полюсов в правой полуплоскости у замкнутой системы.
До появления системы MATLAB использовали номограммы замыкания Найквиста разомкнутой системы и считывалась информация о ЛАФЧХ замкнутой. Замкнутая:
Разомкнутая:
|
40. Основные показатели качества регулирования системы. Их связь с запасами устойчивости.
Показатели качества: 1) tр – время регулирования — время, за которое выходной сигнал перестанет отклоняться более чем на 5% от установившегося. 2)
перерегулирование:
3) N- число колебаний за время регулирования 4)
5) логарифмический декремент затухания 6) максимальная скорость Связь показателей качества с запасами устойчивости: Большие запасы устойчивости: Переходный процесс близкий к апериодическому с уменьшением запасов устойчивости. Переходный процесс монотонный при дальнейшем уменьшении колебаний. Апериодический
:
Монотонный:
Колебательный:
|
|
|
41. (1/3) Определение свободного движения в сист. с пом. обр. преобр. Лапласа выр-я от ненулевых начальных условий.
Можем
исп. Для любого
входного сигнала.
Снимаем ограничения о нулевых н.у.
Преобразования Лапласа
|
41. (2/3) Определение свободного движения в сист. с пом. обр. преобр. Лапласа выр-я от ненулевых начальных условий.
…
Применяем преобразования Лапласа к ур-ю (*) при ненулевых н.у.
Рассмотрим свободное движение системы (на вход ничего не подается g(t)=0). D(s) – корни х.у. сис-мы. Пусть l штук корней простых сод-ся в этом ур-и: 1)
|
41. (3/3) Определение свободного движения в сист. с пом. обр. преобр. Лапласа выр-я от ненулевых начальных условий. 2)
Пусть среди корней имеется r
пар компл.-сопряж. корней
3)
Пусть имеется k
кратных корней кратности
|
|
|
42. Определение вынужденной составляющей движения в системе в системе с помощью обратного преобразования Лапласа от выражения выходного сигнала Y(s).
|
43. Приближенная оценка показателей качества по доминирующим полюсам передаточной функции системы.
Наибольшее влияние на переходный процесс оказывают полюса, находящиеся ближе к мнимой оси. Удаленные полюса мало влияют на переходный процесс, а на качество вообще не влияют можно пренебрегать этими составляющими движения. Вычеты в ближних полюсах больше - полюса доминируют (доминировать могут как действительные, так и комплексные полюса). Оценка времени регулирования: 1)
Если
доминирующий полюс явл. действительным:
Формула для перерегулирования: 2)
|
44. (1/2) Метод корневого годографа (КГ). Метод
корневого годографа позволяет найти
траекторию корней характер-го уравнения
замкнутой сист., в зависимости от коэф.
усиления разомкн. системы при
Команда: rltool(w) Рассм.
Систему
При таком представлении К – истинный коэф. усил
где
Метод КГ позволяет узнать какие корни будут у х.у. замкнутой ситст.. Выражение для замкн. сист.: 1-е представление:
|
|
|
44. (2/2) Метод корневого годографа (КГ).
б)
Для устойчивости системы достаточно, чтобы корни располагались слева. Из а) можно получить 2 ур-я, кот. буд. соответствовать геом. картина: 1-е ур-е – для модулей (длин векторов), 2-е ур-е – для аргументов
(3 полюса, 1 нуль). Через какую точку пройдет хоть одна ветвь КГ-фа? Пусть * - эта точка, через кот. проходит ветвь КГ, тогда должно выполняться:
|
45. (1/2) Правила построения траекторий корней в методе КГ. 1. 1)Кол-во Г-фов =порядку разомкн. сист. 2)Каждая траектория КГ-фа явл-ся непрер. кривой, зависящей от К. Искл.:есть разрывы (в бесконечности) 3)Комплексные части Г-фа всегда сопряжены(можно строить только верх) 2.
Поведение КГ при
3.Поведение
КГ при
А)когда порядок числит.=порядку знамен. m=n
Б)
m<n.
Рассм-м поведение КГ на удаленных
областях пл.S
(
|
45. (2/2) Правила построения траекторий корней в методе КГ. 4.КГ-ф
на вещественной оси опр-ся с помощью
ур-я для аргумента
5.Углы выхода ветвей КГ из компл-сопряж полюсов. Из действит. Может двигаться либо к 0, либо к 180, т.е. движ. по действит. оси. Если кратные двум, то движ вверх или вниз. Если 3, то под углом 120. 6.Точки пересеч ветвей КГ с действительной осью. Либо приходят, либо уходят. 7.Точки пересеч.ветвей КГ с мнимой осью. Записываем х.у. замкн.сист. в след.виде.
2
неизвестных:
8.Когда рас. х.у.замкн.сист. полин. коэф. s при (n-m) степени. Если все звенья в разомкн.сист. с + и не выше 2-го пор., в рез-те замыкания единич. ООС сист. Никогда не станет неуст.. |
|
|
46. (1/2) Анализ и проектирование систем с помощью метода КГ.
S1=0,
1) Имеем 3 ветви траектории, 2 ветви сопряжены; 2) Из полюсов начинается; 3) Все нули на ∞, все КГ закан. на ∞;
l=0
l=1
4) КГ пройдет по тем участкам Re оси, где справа нах-ся нечетное число нулей и полюсов; 5)
углы выхода
|
46. (2/2) Анализ и проектирование систем с помощью метода КГ.
6) Нет пересеч. с Re осью; 7) Нет пересеч. с Im осью.
Строим КГ с ООС. Если ПОС, то: все правила, касающиеся модулей не измен., всё, что связанно с арг., измен. на противоположное. 1)
углы асимптот
2) принадлежит Re оси - - где четное число. |
47. (1/2) Исследование точности регулирования с помощью разложения в степенной ряд передаточной функции ошибки.
Для того, чт. Оценить ошибку, нужно получить выражение перед.ф-и ошибки.
Передат.
ф-я ошибки
Разложим перед.ф-ю ошибки в ряд
t>tраз (при переходе от Лапл. к времен. преобр.) Малая S означает большие времена (зависит от системы), оценка системы провод. по врем. регулирования). Ошибка
|
|
|
47. (2/2) Исследование точности регулирования с помощью разложения в степенной ряд передаточной функции ошибки. Применяем
преобр. Лапласа Наибольший вклад дают первые три слагаемых. Ошибки(по слагаемому): 1-по управлению, 2-по скорости, 3-по ускорению. Приближенное выражение:
|
48.
Исследование точности регулирования
при наличии возмущающего воздействия.
f-помехи; g-полезный управляющий сигнал.
Условие отсутствия статич. ошибки по отношению к постоянному возмущению заключ. В наличии интегратора в W1, а не в W2; хотя, в W2 интегратор мог и находиться. Если интегратор содержится в W2, это означает, что имеем астатизм по отношению к управляющему сигналу.
|
49. Анализ точности регулирования в статической системе.
Разлагаем в ряд (внизу сумма полиномов):
На
вход статической системы подаем
ступеньку g(t)=1(t)
|
|
|
50. Анализ точности регулирования в системах с астатизмом 1-го и 2-го порядка. Астатизм 1-го порядка
Ф(s)
—
подаем на вход
ступеньку
—
подаем линейный
сигнал
Если нужно иссл. систему с пост. скор., то нужен астатизм 1-го порядка. Астатизм
2-го порядка
Ф(s)
— ступенька отрабатывается ε(t)=0 — линейка отрабатывается ε(t)=0 — а с постоянным ускорением Пусть на вход 3-х систем подается G(t)=A1t+A2t2 1 система (по параболе) 2 система(линейно) 3 система (установл.) |
51. (1/3) Повышение точности методом комбинированного управления. При увеличении количества интеграторов: астатизм 1-го порядка получаем ограничение для коэффициентов усиления. Чтобы система была устойчива, годограф не должен охватывать -1.
Астатизм 2-го порядка. Динамические звенья охватывают –1=> система неустойчивая => нужны корректирующие устройства (фазоопережающие цепочки) => обеспечим устойчивость и точность.
Астатизм 3-го порядка. Охватывает -1 => нужна сложная коррекция, при изменении параметров система может стать неустойчивой.
|
51. (2/3) Повышение точности методом комбинированного управления. Метод комбинированного управления повышает точность без ув-я астатизма системы: Структурная схема:
W2 – объект управления и исполнительное устройство. ε(s)= g(s)*((1-Wк W2)/(1+W1 W2) ε= 0 при Wк =W2^(-1) С помощью Wк в системе без астатизма делаем G = 0, с астатизмом 1-го порядка G = 1 и т.д. Нельзя получить инвариантную систему, т.е. чтобы ε не зависила от вида входного сигнала. Нельзя получить систему без ε ,т. К W2 функция реальная, а обратная ей функция может быть физически нереализуема, но повысить точность можно. Оценка точности при наличии возмущающего воздействия. Структурная схема:
|
|
|
51. (3/3) Повышение точности методом комбинированного управления. ε(s)= g(s)*(1/(1+W1 W2)) – ((W2 / (1+W1 W2))* f(s). пусть f(t) = 1(t), чтобы ε(t)= 0 надо : 1/s ввести в W1 , если в W2 есть 1/s , то ((1/s)/(1+W1/s)) => s – сократиться и смысла в ней нет. Условие отсутствия статической ошибки по отношению к возмущению заключается в наличии 1/s в W1 , хотя в W2 может быть 1/s (система обладает астатизмом по отношению к управляющему воздействию, но не по отношению к возмущению.)
|
52. (1/2) Построение желаемой ЛАЧХ следящей системы. Метод синтеза основан на построении желаемой ЛАФЧХ разомкнутой системы. Система слежения ПВО движущимися целями: g(t) – угол на который должна поварач-ся система, чтобы быть направленной на цель. Системы должна быть рассчитана на g’max и g’’max, чтобы ошибка не превышала ε зад., а также tp<=t p зад.и σ max<= σ max.зад. Следящая система должна иметь астатизм хотя бы 1-го порядка => С0 = 0 ε(t) = ε k(t) + εe(t), где ε k(t)- ошибка по скорости, εe(t)- ошибка по ускорению. Большую часть ε зад., отводят на εe(t), а ε k(t) = (30-40)% ε зад., εe(t) = (60-70)% ε зад ε к зад >= g’max/Dω => Dω>= g’max/ ε к зад. ε е зад >= g’’max/Dе => Dе>= g’’max/ ε е зад Хар-ки
системы для удовл-я требований точности.
ωе
=
|
52. (2/2) Построение желаемой ЛАЧХ следящей системы. Н
απ/ωc
= t p
зад
σmax%
= t p.зад => найдём ωc ωc >= απ/ t p.зад . Через ωc проводим линию с наклоном -20дБ/дек, наклон -20дБ/дек должен сохраняться хотя бы в промежутке -17-17 дБ/дек. => обеспечим запасы устойчивости. Чем дольше сохранится -20дБ/дек, тем меньше перерегулирование ωc увеличивается => увеличивается быстродействие. Область ВЧ на ЛАФЧХ зависит от Wн . Пусть ЛАФЧХ для Wн имеет вид - Чтобы получить Wк надо из Wж-Wн. |
|
|
53. Синтез посл коррек уст-ва след системы
- Wк Wн
Wк – сложно изменить, Wн – не меняется Состав Wн: Объект упр-я, измерит уст-во(датчичк), исполнит уст-во, согласующее уст-во(усилитель мощности). Требования к системе: 1) по точности 2)
по обеспечению качества регул-я tр
,
3) какие возмущения влияют на сист и на компенсацию 4) стоимость и надежн сист 5) вес и габаритн размеры уст-в 6) режимы вибрации, температура окр среды, влияние агрессивных сред Для ИУ важны передаваемая и мах момент вращения Метод синтеза основан на построении желаемой ЛАФЧХ разомкнутой системы. |
54. (1/2) Назн корр уст-в в САР. Жесткая и гибкая ОС Wк(S)=(Кк(Т2S+1)(T3S+1))/(S(T1S+1)) Реализуем коррекцию на ОУ:Wк(S)= Wк’(S) * Wк”(S) Wк’(S)=Kк(T2S+1)/S = Кк(T2 + 1/S) : T2 Кк 1/S
Wк”(S) = (T3S+1)/( T1S+1) :
/T1 1/S -
Необходимо
взять 2 интегратора. 1) Огр-е на К в разомкн сист, К растет, растет напряжение входа. При больших К велика вер-ть, что сигналы войдут в насыщ-е, => сист станет нелин => не получим нужн быстродейств. 2) При больших К система начинает усиливать возмущающее действие => система чувствительна к шумам 3)
В Wн
часто содержатся слабодемпфирующие
звенья(колеб звено с малым
В тех случаях, когда есть слабодемпф, неуст, консерват. Звенья, надо строить доп. внутренний контур :
- Wк W1 W2
Woc
|
54. (2/2) Назн корр уст-в в САР. Жесткая и гибкая ОС W1 – слабодемпфирующее звено
После исп-я ОС:
Wос = K/(TS+1), Woc = K – жесткие ОС, т.к. так как в установившемся режиме ос действует. S->0, Woc->K. Гибкая ОС – ОС, кот. Действует только в переходном процессе, а в установивш режиме ее нет, то есть дифф. Звено. При S->0 Woc=0 Woc=KS/(TS+1) – осуществляет демпфирование колебаний. Если в ОС будет 1/S, то не будет передаваться сигнал на выход(плохо, так как нулевая передача). |
|


 x’1(t)
= f1(x1,…,xn
, u1,…,um)
x’1(t)
= f1(x1,…,xn
, u1,…,um) x’(t)
= Ax(t) + Bu(t)
x’(t)
= Ax(t) + Bu(t)


 )
Нелин фун-ия U
Y
)
Нелин фун-ия U
Y

 x
x


 U
Y y=u+v
U
Y y=u+v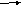 )
)






 )
U
Y
y=
u
– v
)
U
Y
y=
u
– v

 U
Y
U
Y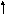

 x´(t)
= Ax(t)
+ Bu(t)
линеаризованная
x´(t)
= Ax(t)
+ Bu(t)
линеаризованная

 _
_
_
_
 ∫x(t)
= ∫Ax(t) + Bu(t) (1)
∫x(t)
= ∫Ax(t) + Bu(t) (1)








 _
_
_
_ x’1
= λ1x1
+ u ┌ λ1
0 …. 0
┐
┌1
┐
x’1
= λ1x1
+ u ┌ λ1
0 …. 0
┐
┌1
┐


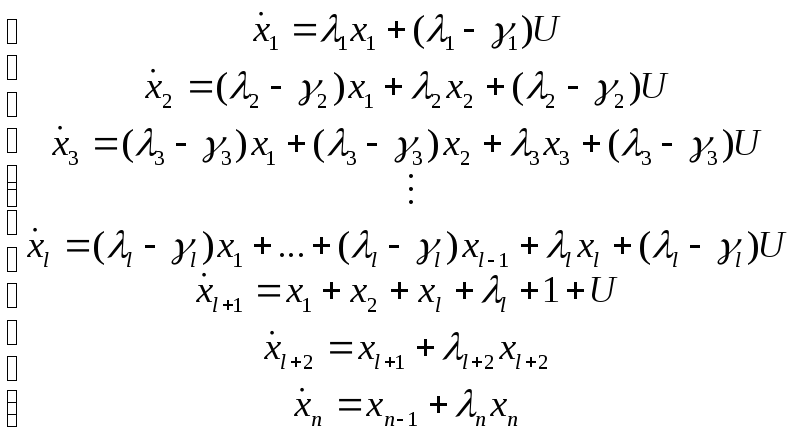

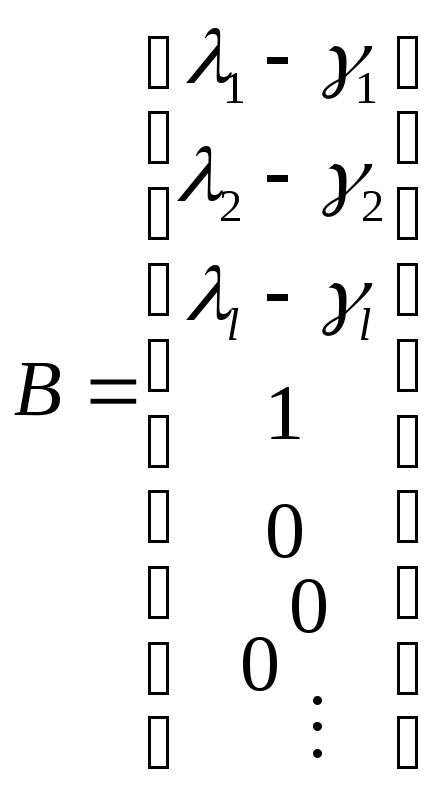







 С=[10…0]
С=[10…0] Пусть
Пусть
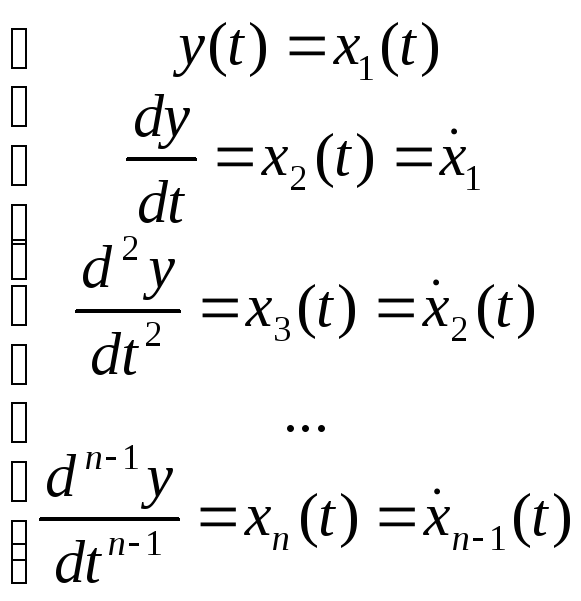



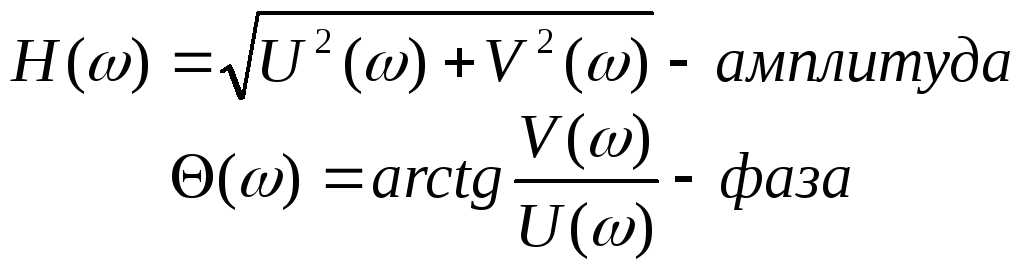
 ;
;

 ЛАФЧХ:
ЛАФЧХ:











 L(ω)=20lg H(ω)
L(ω)=20lg H(ω)
 L(ω)=20lg H(ω)
L(ω)=20lg H(ω)

 ЛАФЧХ:
ЛАФЧХ:



 L(ω)=20lg H(ω)
L(ω)=20lg H(ω)













 где:
а)
где:
а)

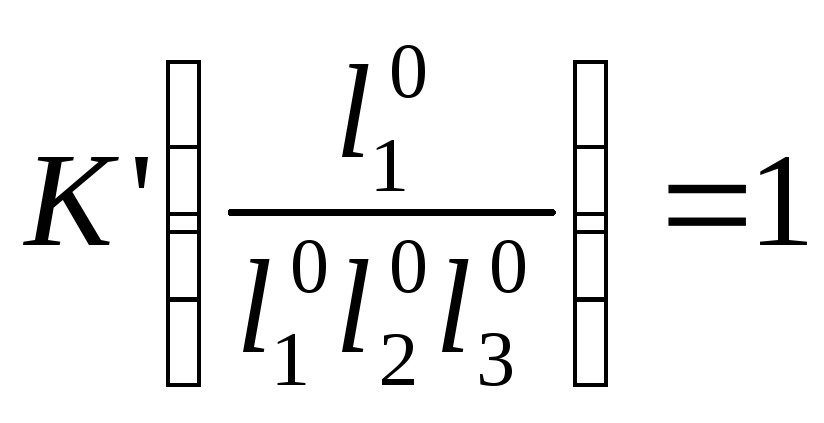
 .
.
 K=K’/2,
K=K’/2,





 (*)
(*)
 После
деления многочленов столбиком получаем:
После
деления многочленов столбиком получаем:


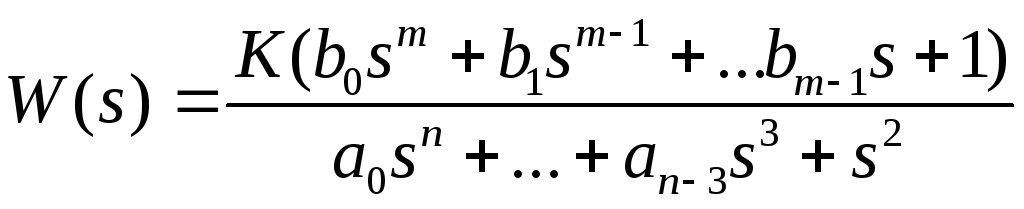






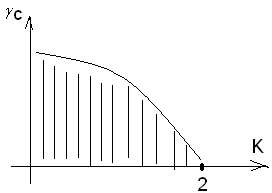
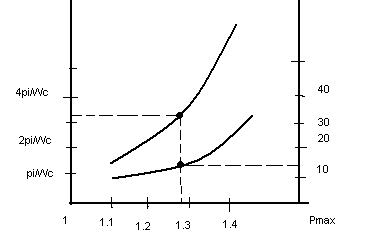 Рmax
– макс значение вещественной частотной
характеристики замкнутой системы.
Ф(jω)
= P(ω)
+ jQ(ω)
απ/ωc
=
Рmax
– макс значение вещественной частотной
характеристики замкнутой системы.
Ф(jω)
= P(ω)
+ jQ(ω)
απ/ωc
=

 T3
T3

