
Иванова. Построение графиков функции
.pdf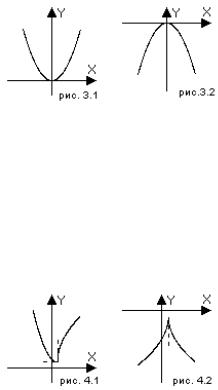
2. Если функция f x |
дважды дифференцируема в точке |
x0 , f x0 0и f x0 0 |
( f x0 0), то точка x0 является |
точкой максимума (минимума).
Для запоминания достаточного условия удобно использо-
вать модельные примеры: y x2 (рис. 3.1) и y x2 (рис. 3.2)
при x0 0имеют максимум и минимум соответственно:
3. Пусть существует 0, такое что функция f x диффе-
ренцируема в проколотой -окрестности точки x0 , непрерывна
в точке x0 . Тогда,
а) если существуют конечные или бесконечные правая и ле-
вая производные в точке |
x0 и |
|
0, |
|
0, то |
x0 |
f x0 |
f x0 |
|||||
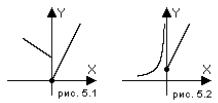
является точкой минимума (рис.4.1). |
|
|
|
|
||
|
|
0, то x0 |
— точка максиму- |
|||
б) если f x0 0, |
f x0 |
|||||
ма (рис. 4.2).
Замечание 2. Из теоремы Лагранжа о среднем следует, что, если
существует окрестность U x0 точки x0 , такая |
что функция f x |
определена и непрерывна в окрестности U x0 , |
дифференцируема в |
13
проколотой окрестности U x0 и существуют конечные или бесконеч-
ные пределы производных справа и слева |
f |
x 0 |
lim f x и |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x x0 0 |
f x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f x , то существуют и правая и левая производная |
||||||||||||
0 |
x x0 0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
f x |
lim |
|
f x f x0 |
|
и |
f x |
|
lim |
f x f x0 |
, и имеют ме- |
|||
0 |
x x0 0 |
x x0 |
x |
0 |
|
x x0 0 |
x x0 |
|
|||||
сто равенства |
f x |
0 |
f |
0 и |
f x |
|
f x 0 . Поэтому, при |
||||||
|
|
|
|
|
0 |
|
|
0 |
|
0 |
|
||
построении графиков функций для доказательства наличия экстремума в точке разрыва производной исследуемой функции как правило рассматривают пределы производных справа и слева. Предел производной справа (слева) равен тангенсу угла наклона касательной справа (слева) в точке экстремума.
Замечание 3. Точка разрыва первого и второго рода функции f x может быть точкой локального экстремума (рис. 5.1 и
5.2).
5. Выпуклость функции вверх и вниз. Точки перегиба Определение 5. Непрерывная функция y f x называется
выпуклой вверх (строго выпуклой вверх) на отрезке a,b , если
для любых различных точек |
|
x1 |
и x2 |
отрезка a,b выполняется |
|||||||||||||
неравенство |
f x f x |
|
|
|
|
|
|
|
f x f x |
|
|
||||||
x x |
2 |
|
2 |
|
x x |
2 |
|
2 |
|||||||||
f |
1 |
|
1 |
|
|
f |
1 |
|
1 |
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Определение 6. Непрерывная функция |
y f x |
называется |
||||||||||||||
выпуклой вниз (строго |
выпуклой вниз) на отрезке a,b , если |
||||||||||||||||
14
для любых различных точек x1 и x2 отрезка a,b выполняется неравенство
f x1 2x2 f x1 2 f x2 f x1 2x2
f x1 2 f x2 .
Из |
определений следует, что непрерывная функция |
y f x |
называется выпуклой вверх (строго выпуклой вверх) на |
отрезке a,b , если каждая точка любой хорды к графику функ-
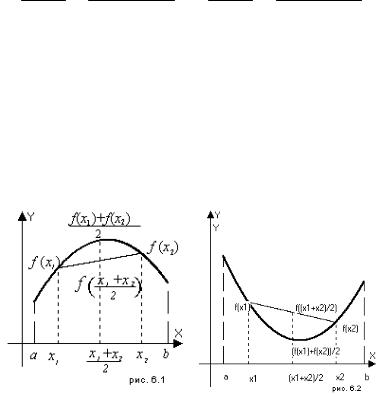
ции y f x лежит не выше (ниже) графика y f x (рис. 6.1). Непрерывная функция y f x называется выпуклой вниз
(строго выпуклой вниз) на отрезке a,b , если каждая точка лю-
бой хорды к графику функции y f x лежит не ниже (выше)
графика y f x (рис. 6.2).
Достаточные условия выпуклости вверх и вниз функции
y f x на отрезке: |
|
существует на отрезке a,b , |
||
Пусть f x |
||||
|
x — на интервале a,b . |
|
|
|
а f |
|
x a,b , то функ- |
||
|
|
|
|
|
|
1. Если f x 0 |
( f x 0)при всех |
||
ция выпукла вверх (строго выпукла верх) на отрезке a,b .
15
|
x 0 ( f |
|
x a,b , то функ- |
2. Если f |
x 0) при всех |
ция выпукла вниз (строго выпукла вниз) на отрезке a,b .
Определение 7. Точка x0 называется точкой перегиба функ-
ции y f x , если:
1.Функция y f x непрерывна в точке x0;
2.Функция y f x имеет в точке x0 конечную или бес-
конечную определенного знака производную;
3. Функция y f x при переходе через точку x0 меняет направление выпуклости, то есть существует 0, такое что на
одном из интервалов x0 ,x0 , x0,x0 |
функция выпукла |
||||
вверх, а на другом выпукла вниз. |
|
|
|||
Определение 8. Точка x0, f x0 |
называется точкой пере- |
||||
гиба графика |
функции y f x , если |
x0 — точка перегиба |
|||
функции y f x . |
|
|
|
||
Необходимое условие перегиба в точке x0. |
|
||||
Если |
x0 — точка перегиба функции y f x и функция |
||||
y f x |
имеет в некоторой окрестности точки |
x0 вторую про- |
|||
изводную, непрерывную в точке x0, то f x0 0. |
|||||
Достаточные условия перегиба в точке x0. |
|||||
1. Если функция |
y f x непрерывна в окрестности точки |
||||
x0, имеет в точке x0 |
конечную или бесконечную определенно- |
||||
|
|
|
|
|
|
го знака производную, а функция f x определена в проколотой |
|||||
окрестности точки x0 |
и меняет знак при переходе через эту точ- |
||||
ку, то x0 — точка перегиба функции y f x . |
|
||||
2. Если |
f x0 |
0, а f x0 0, то x0 — точка перегиба |
|||
функции y |
f x . |
|
|
|
|
16
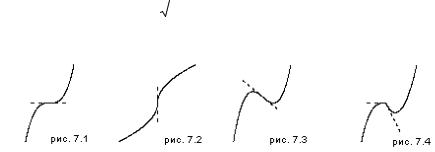
В |
качестве модельных |
примеров |
рассмотрим функции |
||
y x3 |
(рис. 7.1) и y 3 |
|
|
(рис. 7.2). Дополнительно рассмот- |
|
x |
|||||
рим еще два примера перегиба (рис. 7.3 и |
7.4). |
||||
Замечание 4. Если функция y f x дважды дифференци-
руема в окрестности точки x0, и x0 — точка перегиба функции y f x , то график функции переходит с одной стороны касательной на другую. Обратное неверно.
Пример 9. Доказать, что, из того, что график функции y f x в точке x0 переходит с одной стороны касательной на другую не следует, что точка x0 является точкой перегиба функ-
ции y f x . |
|
|
|
|
|
|
|
1 |
|
3 |
|
|
2 sin |
|
x |
|
,x 0; |
|
|
||||
► Рассмотрим функцию f x |
|
x |
|
. В точке |
|
0,x 0
x0 0 график функции имеет горизонтальную касательную, и
переходит с одной стороны касательно на другую, но точка x0 не является точкой перегиба функции f x , так как не существует левой и правой окрестностей точки x0, в которых сохраняется направление выпуклости функции f x . ◄
3. Дифференцирование функции, аналитическое выражение которой содержит модуль
17
1) При исследовании с помощью производной поведения графика функции, аналитическое выражение которой содержит модуль, удобно производить дифференцирование по правилу
сложной функции, учитывая, что |
|
x |
|
|
sign x |
во всех точках |
||||
|
|
|||||||||
|
|
|
||||||||
дифференцируемости функции y |
|
x |
|
. |
|
y f x sign x |
||||
|
|
|
||||||||
2) При дифференцировании функции вида |
||||||||||
во всех точках дифференцируемости функции справедлива фор-
мула y |
|
sign x, так как производная функции сигнум |
f x |
равна нулю во всех точках дифференцируемости.
Пример 10. Найти первую и вторую производные функции
f x |
|
x 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
sign |
|
x 2 |
|
, |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
► f x |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f x |
4 |
|
x 2 |
|
3 2 |
sign |
|
|
x 2 |
|
4 |
|
x 2 |
|
3 2 |
при x 2.◄ |
|||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4.Основные требования к результатам исследования
ипостроению графика
1.Все результаты исследования функции следует обосновать в ходе решения. Все исследования функции, включая все необходимые вычисления: вычисления пределов функции, вычисления производных, решения уравнений, являются необходимой частью решения задачи на построение графика функции или кривой.
2.Все результаты должны быть получены точно. Необходимые приближенные вычисление привести в решении задачи.
3.Масштаб построения графика следует выбирать так, чтобы были отражены основные характерные моменты поведения графика функции.
4.На рисунке изобразить вертикальные и наклонные асимптоты, указать уравнения асимптот.
18
5.Обозначить точки минимума и максимума функции, указать их координаты.
6.Обозначить точки разрыва производной, указать их координаты. Изобразить односторонние касательные (если они существуют). В случае существования конечной односторонней производной указать тангенс угла наклона односторонней касательной.
7.Обозначить точки перегиба графика функции, указать их координаты. Указать точное значение производной или тангенс угла наклона касательной в точке перегиба. Изобразить касательную к графику функции в точке перегиба.
19

5. Примеры исследования функций и построения графиков функций.
Пример 1. Исследовать функцию |
f x |
x3 |
и построить |
|
x 1 2 |
||||
ее график. |
|
|
||
;1 1; . |
||||
► Область определения функции Df |
||||
Асимптоты.
Вертикальная асимптота x 1.
Для нахождения наклонной асимптоты можно использовать различные методы. Во-первых, уравнение асимптоты можно получить методом выделения главной части, как частное от деления
x3 |
на x 1 2 , выполнив его, например, "уголком", или исполь- |
|
зуя |
|
представление |
x3 x 1 1 3 x 1 3 3 x 1 2 o x 1 2 |
, или представляя |
|
x3 |
по формуле Тейлора в окрестности точки |
x 1. Асимптотой |
графика функции при x и при x является прямая y x 2.
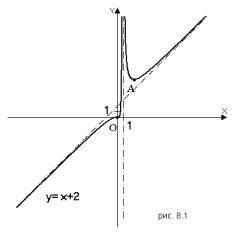
Строим эскиз. Изображаем оси координат и асимптоты. Из
3x 2
равенства f x x 2 x 1 2 , следует, что при x гра-
фик функции стремится к асимптоте y x 2 снизу, так как
3x 2
x 1 2 0; при x график функции стремится к асимпто-
3x 2
те y x 2 сверху, так как x 1 2 0. Можно предположить,
что график функции при достаточно больших отрицательных значениях аргумента имеет направление выпуклости к асимптоте, то есть вверх.
При стремлении к асимптоте x 1 слева функция стремится к . Можно предположить, что график функции в достаточно
20
малой левой окрестности точки x 1 является выпуклым вниз (к асимптоте).
При стремлении к асимптоте x 1 справа функция стремится к . Можно предположить, что график функции в достаточно малой правой окрестности точки x 1 также является выпуклым вниз (к асимптоте).
Так как на промежутке x 1функция дифференцируема и меняет направление выпуклости, то на этом промежутке должна быть точка перегиба. Эскиз графика изображен на рис. 8.1.
Найдем первую и вторую производные функции
|
x |
2 |
x 3 |
|
|
|
x |
2 |
x 3 |
|
|
6x |
|||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
; |
|
|
3 |
|
4 . |
||||||
f x |
|
|
|
f x |
|
|
|
|
|
||||||
|
x 1 |
|
|
|
x 1 |
|
|
x 1 |
|||||||
Анализ результатов исследования. Результаты исследования удобно объединить в виде таблицы. Первая колонка таблицы содержит все промежутки и особую точку x 1 графика функции, а также точки, в которых равны нулю или не существуют первая или вторая производные.
21
|
|
y x |
y x |
y x |
Выводы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3; |
~ x 2 |
|
|
, асимптота |
|
A |
3 |
27 4 |
0 |
|
точка локального |
|
|
|
|
|
|
минимума |
|
|
1;3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
вертикальная асим- |
|
|
|
|
|
|
птота |
|
|
0;1 |
|
|
|
|
|
C |
0 |
0 |
0 |
0 |
точка перегиба |
с |
|
|
|
|
|
горизонтальной |
ка- |
|
|
|
|
|
сательной |
|
|
;0 |
~ x 2 |
|
|
, асимптота |
|
Замечание. При заполнении таблицы следует иметь в виду, что:
1)в таблицу мы вносим существенные для построения графика выводы, заполнение всех клеточек не обязательно;
2)если в таблицу вносим числовое значение, то оно должно быть точным, далее можно указать приближенное значение;
3)на этапе заполнения таблицы и построения графика целесообразно проверить согласованность полученных результатов исследования.
График функции изображен на рис. 8.2.
22
