
Vse_bilety_BEZ_dokazatelstv
.pdfРасстояние между скрещивающимися прямыми.
Пусть прямые p и q не параллельны. Известно, что в этом случае существуют такие параллельные плоскости P и Q, что прямая p лежит в P, а прямая q в Q. Расстояние h между P и Q называется расстоянием между прямыми p и q. Если p и q пересекаются, то P и Q совпадают и h = 0.
Для того чтобы найти расстояние h, проще всего разделить объем параллелепипеда, построенного на векторах 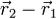 ,
, 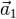 и
и 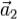 , на площадь его
, на площадь его
основания. Мы получим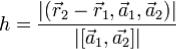
21. Общее решение системы линейных алгебраических уравнений.
Теорема. Если 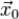 - некоторое решение системы
- некоторое решение системы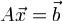 ,
,
а F - фундаментальная матрица её приведенной системы, то столбец 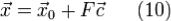 при любом
при любом 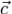 является решением системы (1). Наоборот, для каждого её решения
является решением системы (1). Наоборот, для каждого её решения  найдется такой столбец
найдется такой столбец 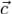 , что оно будет представлено формулой (10).Выражение, стоящее в правой части формулы (10), называется общим решением системы линейных уравнений.
, что оно будет представлено формулой (10).Выражение, стоящее в правой части формулы (10), называется общим решением системы линейных уравнений.
Если 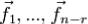 - фундаментальная система решений, а c1,...,cn •| r - произвольные постоянные, то формула (10) может быть написана так:
- фундаментальная система решений, а c1,...,cn •| r - произвольные постоянные, то формула (10) может быть написана так: 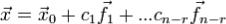 .
.
Это теорема верна, в частности, и для однородных систем, если  - тривиальное решение.
- тривиальное решение.
Теорема Кронекера-Капелли.
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Иначе утверждение теоремы можно сформулировать так: приписывание к матрице A размеров  стобца
стобца 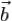 высоты m не меняет её ранга тогда и только тогда, когда этот столбец - линейная комбинация столбцов A.
высоты m не меняет её ранга тогда и только тогда, когда этот столбец - линейная комбинация столбцов A.
22. Линейное отображ конечномерных лин пространств, его матрица.
Определение. Пусть 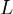 и
и  - два линейных пространства, оба вещественные или оба комплексные. Под отображением A пространства
- два линейных пространства, оба вещественные или оба комплексные. Под отображением A пространства 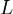 в пространство
в пространство  понимается закон, по которому каждому вектору
понимается закон, по которому каждому вектору
из Lсопоставлен единственный вектор из 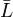 . Мы будем писать
. Мы будем писать 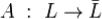 . Образ вектора x обозначаетсяA(x)
. Образ вектора x обозначаетсяA(x)
Определение. Отображение 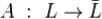 называется линейным, если для любых векторов x и y из L и любого числа α выполнены равенства
называется линейным, если для любых векторов x и y из L и любого числа α выполнены равенства
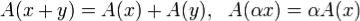 .
.
Определение. Матрицей линейного отображения 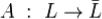 в паре базисов e и f называется матрица, столбцы которой (в их естественнм порядке) - координатные столбцы векторов A(e1),...,A(en) в базисе f.
в паре базисов e и f называется матрица, столбцы которой (в их естественнм порядке) - координатные столбцы векторов A(e1),...,A(en) в базисе f.
Теорема. При линейном отображение 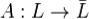 линейное подпространство
линейное подпространство  переходит в линейное подпространство
переходит в линейное подпространство 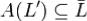 , причем
, причем 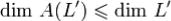 .
.
Определение. Ядро отображения - множество всех векторов переходящих в нулевой вектор при отображении.
Теорема. Ядро есть линейное подпространство.
Определение. Отображение при котором различные вектора имеют различные образы называется инъективным.
Теорема. Отображение инъективно тогда и только тогда, когда ядро есть нулевое подпространство.
Св-а собств векторов и собственных значений линейных преобразований.
Линейное преобразование - это отображение, которое отображает линейное пространство в то же самое протстранство.
Определение. Если для числа λ подпространство Ker(A •| λE) ненулевое, то λ называется собственным значением преобразования, а подпространство - собственным подпространством, соответствующим собственному значению λ.
Определение. Вектор x называется собственным вектором преобр-я A,
соответствующим собственному значению λ, если: 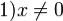 ; 2)A(x) = λx. Предположение 5. Собственные вектора и только они являются базисными векторами одномерных подпространств, инвариантных относительно A. Предположение 6. В i-м столбце матрицы линейного преобразования все элементы вне главной диагонали равны нулю тогда и только тогда, когда i-й базисный вектор собственный. В этом случае диагональный элемент столбца - собственное значение.
; 2)A(x) = λx. Предположение 5. Собственные вектора и только они являются базисными векторами одномерных подпространств, инвариантных относительно A. Предположение 6. В i-м столбце матрицы линейного преобразования все элементы вне главной диагонали равны нулю тогда и только тогда, когда i-й базисный вектор собственный. В этом случае диагональный элемент столбца - собственное значение.
23. Самосопряженные преобразования евклидовых пространств, свойства их собственных значений и собственных векторов.
Линейное преобразование A евклидова пространства называется самосопряженным, если A = A * . Это равносильно тому, что (A(x),y) = (x,A(y)) для любых x и y.
Теорема 1. Все корни характеристического многочлена самосопряженного преобразования вещественны.
Теорема 2. Собственные подпространства самосопряженного преобразования попарно ортогональны.
Теорема равносильна следующему утверждению.
Если собственные векторы самосопряженного преобразования принадлежит различным собственным значениям, то они ортогональны. Теорема 3. Если подпространство  инвариантно относительно самосопряженного преобразования A, то ортогональное
инвариантно относительно самосопряженного преобразования A, то ортогональное
дополнение 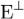 этого подпространства - также инвариантно относительно A. Теорема 4. Пусть A - самосопряженное преобразование евклидова пространства Ε. Тогда в Ε существует ортонормированный базис из собственных векторов A.
этого подпространства - также инвариантно относительно A. Теорема 4. Пусть A - самосопряженное преобразование евклидова пространства Ε. Тогда в Ε существует ортонормированный базис из собственных векторов A.
Из теоремы 3 следует, что ортогональное дополнение L также инвариантно.
24. Приведение квадратичных форм в линейном пространстве к каноническому виду.
Определение. Квадратичной формой или квадратичной функцией на линейном пространстве L называется функция k, значение которой на любом векторе x определяется равенством k(x) = b(x,x), где b -
симметричная билинейная функция .
Определение. Матрицей квадратичной формы называется матрица соответствующей билинейной функции.
Мы имеем следующее выражение значения квадратичной формы через координатный столбец вектора: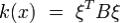
Теорема 1. Для каждой квадратичной формы k существует базис, в котром она имеет диагональный вид.
25. Положительно определенные квадратичные формы.
Определение. Квадратичную форму k будем называть положительно определенной на подпространстве L'пространства L, если k(x) > 0 для любого ненулевого вектора x из L'.
Если говорят, что квадратичная форма положительно определена без уточнения подпространтсва, то она обладает таким свойством на всем L. Теорема. Для положительной определенности квадратичной формы необходимо и достаточно, чтобы миноры её матрицы удовлетворяли
неравенствам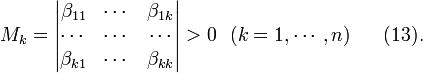 Миноры вида (13) называются главными минорами матрицы.
Миноры вида (13) называются главными минорами матрицы.
26.Когда правая часть является квазимногочленом.Рассмотрим уравнение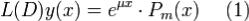 ,гдеμ - заданное комплексное число, Pm(x) - заданный многочлен степени m.
,гдеμ - заданное комплексное число, Pm(x) - заданный многочлен степени m.
Определение. Если число μ является корнем характеристического уравнения L(λ) = 0, то говорят, что в уравнении (1) имеет место резонансный случай.
Теорема. Для уравнения (1) существует и единственно решение вида 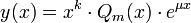 где Qm(x) - многочлен одинаковой с Pm(x) степени m, а число k равно кратности корня μ характеристического уравнения L(λ) = 0 в резонансном случае и k = 0 в нерезонансном.
где Qm(x) - многочлен одинаковой с Pm(x) степени m, а число k равно кратности корня μ характеристического уравнения L(λ) = 0 в резонансном случае и k = 0 в нерезонансном.
27. Системы линейных однородных уравнений с постоянными коэффициентами, методы их решения.
Рассмотрим нормальную линейную однородную систему 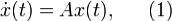 где
где 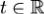 , A - квадратная комплексная матрица порядка n, x(t) - неизвестная вектор-функция с nкомпонентами. Лемма 1. Если x(1)(t),x(2)(t) решения системы (1), а C1,C2 - произвольные комплексные числа, то вектор-функция x(t) = C1x(1)(t) + C2x(2)(t) также решение системы (1).
, A - квадратная комплексная матрица порядка n, x(t) - неизвестная вектор-функция с nкомпонентами. Лемма 1. Если x(1)(t),x(2)(t) решения системы (1), а C1,C2 - произвольные комплексные числа, то вектор-функция x(t) = C1x(1)(t) + C2x(2)(t) также решение системы (1).
Лемма 2. Для того, чтобы вектор-функция x(t) = eλth была нетривиальным решением системы (1), необходимо и достаточно, чтобы λ было собcтвенным значением, а h - соответствующим ему собственным вектором преобразования A.
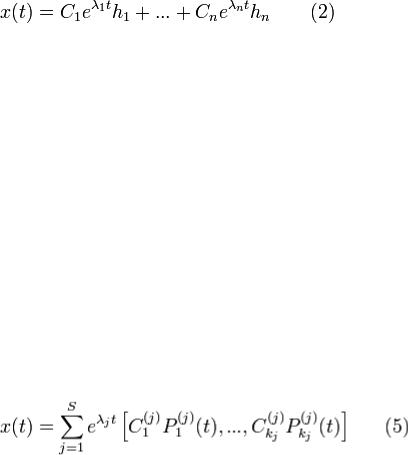
Теорема. Пусть существует базис 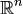 из собственных
из собственных
векторов h1,...,hn линейного преобразования A и пусть λ1,...,λn - соответствующие им собственные значения.Тогда:
а) Вектор-функция x(t) вида
где C1,...,Cm произвольные комплексные постоянные, является решением системы (1).
б)Если x(t) - какое-либо решение системы (1), то найдутся такие значения постоянных C1,...,C2, при которыхx(t) задается формулой (2).
Лемма 3. Каждая из вектор-функций 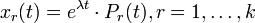 является
является
решением системы (1), где 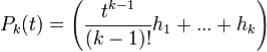 , где
, где 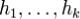 - некоторая жорданова цепочка дляλ.
- некоторая жорданова цепочка дляλ.
Теорема. Пусть жорданов базис в 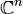 состоит из S жордановых
состоит из S жордановых
цепочек 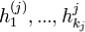 длин kj(k1 + ... + kS =n) для собственных значений λj преобразования A, j = 1,...,S.Тогда:
длин kj(k1 + ... + kS =n) для собственных значений λj преобразования A, j = 1,...,S.Тогда:
а) вектор - функция фида
б) если x(t) - какое-либо решение системы (1), то найдется такой
набор 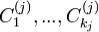 при котором x(t)задается в форме (5).
при котором x(t)задается в форме (5).
28. Линейные обыкновенные дифференциальные уравнения с переменными коэффициентами.
Рассмотрим линейную неоднородную систему где
где 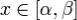 - заданная непрерывная
- заданная непрерывная
на [α,β] квадратная матрица порядка n, f(x) - заданная непрерывная
на [α,β] вектор-функция с n компонентами.Непосредственно проверяется следующее предложение, называемое принципом суперпозиции для системы (1).
Лемма. Если 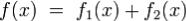 , y1(x) - решение системы (1) при условии
, y1(x) - решение системы (1) при условии 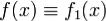 иy2(x) - решение системы (1) при усоловии
иy2(x) - решение системы (1) при усоловии ,
,
то y(x) = y1(x) + y2(x) - решение системы (1).Если известно какое-либо частное решение (1), то интегрирование линейной неоднородной системы (1)
сводится к интегрированию соответствующей (1) линейной однородной системы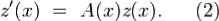
Теорема 1. Пусть y0(x) - некоторое частное решение (1), и Φ(x) - фундаментальная матрица (2). Тогда все решение системы (1) задаются формулой ,где c - произвольный n-мерный вектор. Теорема 2. Если Φ(x) - фундоментальная матрица линейной однородной системы (2), то общее решение линейной неоднородной системы (1) при
,где c - произвольный n-мерный вектор. Теорема 2. Если Φ(x) - фундоментальная матрица линейной однородной системы (2), то общее решение линейной неоднородной системы (1) при
всех 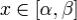 задается формулой
задается формулой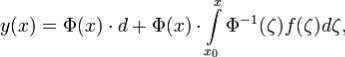 где
где 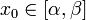 и d - произвольный числовой n - мерный вектор.
и d - произвольный числовой n - мерный вектор.
Фундаментальная система решений.
Определение. Матрица Φ(x) у которой столбцы образуют фундаметальную систему решений (1)  называется фундоментальной матрицей системы (1).
называется фундоментальной матрицей системы (1).
Таким образом,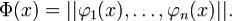
Очевидно, что Φ(x) - непрерывно дифференцируемая матрица на [α,β]. Из теоремы 2 следует, что для (1) существует бесконечно много фундометальных матриц. Из определения фундоментальной системы решений получаем, что Φ(x) - невырожденная матрица на [α,β]. Из теоремы 3 получаем самое важное свойство Φ(x). Именно, если Φ(x) - фундоментальная матрица (1), то общее решение системы (1) записывается в простом виде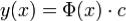 ,где c-произв числовой n-мерный вектор.
,где c-произв числовой n-мерный вектор.
Определитель Вронского. Формула Лиувилля-Остроградского.
Пусть  - система вектор-функций с n компонентами на [α,β]. Определение. Определителем Вронского системы
- система вектор-функций с n компонентами на [α,β]. Определение. Определителем Вронского системы наз.
наз. 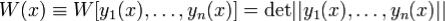 .
.
Теорема. Пусть W(x) - вронскиан решений  системы (1) и пусть
системы (1) и пусть 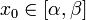 . Тогда для
. Тогда для 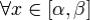 имеет место формула Лиувилля-
имеет место формула Лиувилля-
Остроградского ,где
,где 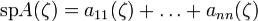 наз ывается следом матрицы A(ζ).
наз ывается следом матрицы A(ζ).
29.Простейшая задача вариационного исчисления. Уравнение Эйлера.
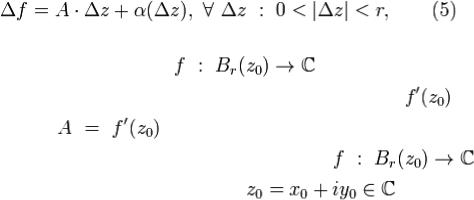
Обозначим через 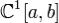 множество всех непрерывно дифференцируемых функций, заданных на [a,b]. Для
множество всех непрерывно дифференцируемых функций, заданных на [a,b]. Для 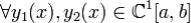 введем расстояние
введем расстояние
между ними 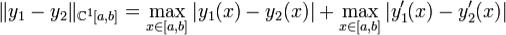 Множество функций C1[a,b] с введенной метрикой является линейным нормированным пространством.
Множество функций C1[a,b] с введенной метрикой является линейным нормированным пространством.
Пусть F(x,y,p) - заданная непрерывно дифференцируемая функция
для 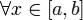 и
и  . Рассмотрим
. Рассмотрим 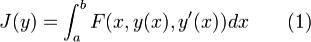 на множестве M тех функций
на множестве M тех функций 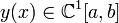 , которые удовлетворяют граничным условиям
, которые удовлетворяют граничным условиям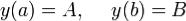 ,где A и B заданные числа. Функции
,где A и B заданные числа. Функции  будем называть допустимыми.
будем называть допустимыми.
Определение. Говорят, что функция 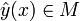 дает слабый локальный минимум функционала (1), если
дает слабый локальный минимум функционала (1), если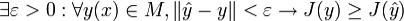 .
.
Определение. Задача нахождения слабого локального экстремума функционала (1) называетсяпростейшей вариационной задачей.
Теорема. Пусть функция F(x,y,p) - дважды непрерывно дифференцируема при 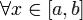 и
и 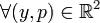 . Если дважды непрерывно дифференцируемая функция
. Если дважды непрерывно дифференцируемая функция 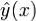 явл. решением простейшей вариационной задачи, то необх,
явл. решением простейшей вариационной задачи, то необх,
чтобы ф-ия 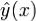 на [a,b] удовлетворяла ур-ию Эйлера
на [a,b] удовлетворяла ур-ию Эйлера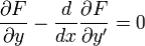
33. Дифф-сть ф-ии комплексного переменного. Условия Коши-Римана.
Определение. Говорят, что функция  дифференцируема в точке
дифференцируема в точке 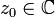 , если справедливо представление
, если справедливо представление
где A не зависит от |
z, а функция α( |
z) является o( z). |
||
Лемма 1. Функция |
дифференцируема в точке z0 тогда и |
|||
только тогда, когда существует производная |
, причем в формуле |
|||
число |
. |
|
|
|
Теорема 1. Для того, чтобы функция |
|
была |
||
дифференцируема в точке |
, н. и д., чтобы |
|||
1)функция u(x,y) и v(x,y) были дифференцируемы в точке  .
.
2)в точке (x0,y0) были выполнены условия Коши-Римана

При этом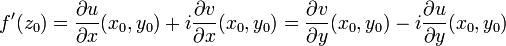
Интегральная теорема Коши.
Теорема. Пусть функция f(z) дифференцируема в односвязной области D и её производная непрерывна в D. Тогда интеграл от f(z) по любой замкнутой
кривой γ, лежащей в области D, равен нулю: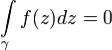 .
.
34. Интегральная формула Коши.
Пусть функция f(z) дифференцируема в односвзяной области D и пусть простая замкнутая кривая γ лежит вD и ориентирована положительно. Тогда для любой точки z, лежащей внутри γ, справедлива формула
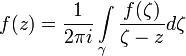 - это называется интегральной формулой Коши.
- это называется интегральной формулой Коши.
Разложение функции, регулярной в окрестности точки, в ряд Тейлора.
Если функция f регулярна в круге Br(a), где 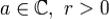 , то она представима в этом круге Br(a) в виде суммы сходящегося ряда Тейлора, т.е.
, то она представима в этом круге Br(a) в виде суммы сходящегося ряда Тейлора, т.е.
 ,где
,где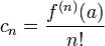 .
.
35. Разложение функции, регулярной в кольце в ряд Лорана.
Всякая функция ω = f(z), регулярная в кольце ρ < | z •| a | < R,
где 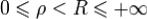 , представима в этом кольце суммой сходящегося ряда
, представима в этом кольце суммой сходящегося ряда
Лорана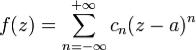 ,коэффициенты которого определяются по
,коэффициенты которого определяются по
формулам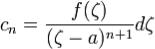 , где
, где 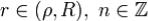 ,
,
причем ориентация окружности | ζ •| a | = r положительная.
Изолированные особые точки однозначного характера.
Определение 1. Пусть функция f не регулярна в точке 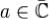 , но регулярна в некоторой проколотой окрестности этой точки. Тогда точку a называют изолированной особой точкой функции f.
, но регулярна в некоторой проколотой окрестности этой точки. Тогда точку a называют изолированной особой точкой функции f.
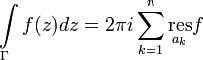
Определение 2. Изолированная точка 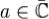 функции
функции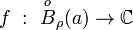 называется1)устранимой особой точкой, если существует конечный предел
называется1)устранимой особой точкой, если существует конечный предел 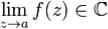 ; 2)полюсом, если существует
; 2)полюсом, если существует 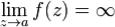 ;
;
3)существенно особой точкой, если не существует конечного или бесконечного предела 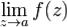 .
.
36. Вычеты.
Определение 1. Пусть  - изолированная особая точка регулярной
- изолированная особая точка регулярной
функции 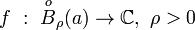 . Пусть
. Пусть 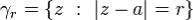 - положительно ориетированная окружность, причем 0 < r < ρ. Тогда вычетом функции f в
- положительно ориетированная окружность, причем 0 < r < ρ. Тогда вычетом функции f в
точке a называется число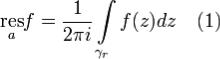
Для получения более удобных выражений вычисления вычета функции,
представим функцию 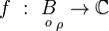 её рядом Лорана с центром в точке a
её рядом Лорана с центром в точке a
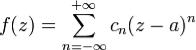 .Получаем, что интеграл (1) равен коэффициенту c •| 1.
.Получаем, что интеграл (1) равен коэффициенту c •| 1.
Определение 2. Пусть функция 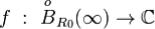 регулярна. Тогда вычетом
регулярна. Тогда вычетом
функции f в бесконечности называется число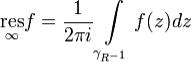 Удобно записывать в виде
Удобно записывать в виде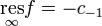
Лемма 1. Пусть a - полюс функции f порядка 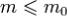 . Тогда справедлива
. Тогда справедлива
формула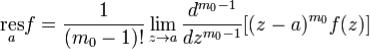
Вычисление интегралов по замкнутому контуру при помощи вычетов
Пусть дана область 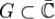 с кусочно-гладкой положительно ориетированной границей Γ. Пусть функция f определена и регулярна на G всюду, за исключением конечного числа изолированных особых точек
с кусочно-гладкой положительно ориетированной границей Γ. Пусть функция f определена и регулярна на G всюду, за исключением конечного числа изолированных особых точек 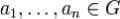 и пусть к тому же функция f непрерывно продолжима на границу области G.
и пусть к тому же функция f непрерывно продолжима на границу области G.
Тогда справедлива формула |
. |
