Электронная структура кристаллических твёрдых веществ.

Электронная структура атомов и молекул.

Известно, что электронная структура атома характеризуется дискретным спектром разрешённых значений энергий электронов: энергетический спектр энергий отдельного атома находится из решения стационарного уравнения Шредингера. Известно, что точное решение нахождения спектра энергий многоэлектронного атома не существует, однако хорошим приближением, которое достаточно точно описывает электронную структуру и химические свойства атомов, является одноэлектронное приближение. Основу этого приближения представляет точное решение уравнения Шредингера для атома водорода, согласно которому электронная структура атома определяется тремя квантовыми числами: главным квантовым число n = 1, 2, …, орбитальным квантовым числом l = 0, 1, … (n - 1) и магнитным квантовым числом m = 0, ± 1, …, ± l.

Главное квантовое число определяет спектр энергий водородоподобного атома по формуле:

где - приведённая масса атома,Z – заряд ядра. Орбитальное и магнитное квантовые числа определяют заполнение квантовых состояний в соответствии с принципом Паули (в одном квантовом числе nlm может быть не более двух электронов с противоположными значениями спина ±) и эмпирическим правилом Хунда, согласно которому электроны занимают квантовые состояния так, чтобы реализовать максимально возможное значение суммарного спина системы.

Каждое электронное квантовое состояние характеризуется волновой функцией φlm(r), квадрат модуля которой определяет пространственное распределение электронной плотности. Характерный вид этих распределений для различных l и m показан на рис.

s – электроны p – электроны, l = 1

(l = 0, m = 0) m = 1 m = 0 m = +1

d – электроны, l = 2

m = -2 m = -1 m = 0 m = 1 m = 2

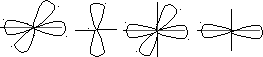
f – электроны, l = 3

m = -3 m = 2 m = -1 m = 0 m = +1 m = +2 m = +3

Межатомные взаимодействия.

Зонная теория.

Совершенно очевидно, что электронная структура твёрдого тела, которое представляет собой регулярную систему сильно взаимодействующих между собой атомов (или молекул) должна сильно измениться по сравнению с электронной структурой отдельных его составляющих, т.е. атомов и молекул.

Теория электронной структуры кристаллических твёрдых тел получила название зонной теории. Основные положения зонной теории сводятся к тому, что вместо дискретных уровней энергии в твёрдом теле появляются энергетические зоны, разрешённые и запрещенные для заполнения электронами. Характер заселённости энергетических зон определяет электронные свойства твёрдого тела.

Возникновение энергетических зон можно объяснить на качественном уровне следующим образом. Каждый энергетический уровень квантовой системы, состоящей из N невзаимодействующих атомов (молекул) в силу их тождественности (принцип квантовой неразличимости одинаковых частиц) является N-кратно вырожденным. Взаимодействия между частицами за счёт их сближения приводит к расщеплению этих уровней в квазинепрерывную энергетическую зону. Так как в изолированных атомах (молекулах) электронами заполнены только нижние уровни, то в твёрдом теле соответствующие нижние зоны будут заполнены (полностью или частично), а более высокие зоны будут свободны. Как правило, электронные свойства твёрдого тела в основном определяют высшая заполненная зона и низшая свободная зона, которые называют соответственно валентной зоной и зоной проводимости. Разность между нижней энергией зоны проводимости и верхней энергией валентной зоны называют шириной запрещённой зоны. Граничная энергия, разделяющая заполненные и незаполненные электронами уровни энергии называется энергией Ферми. Типичные схемы взаимного расположения валентной зоны и зоны проводимости для диэлектриков, полупроводников и металлов показаны на рис.

В диэлектриках ширина запрещённой зоны составляет величину порядка нескольких электроновольт, в полупроводниках порядка 1 эв, а в металлах – равна нулю, при этом энергия Ферми находится внутри частично заполненной зоны. Это происходит либо в силу того, что наивысшая зона заполнена лишь наполовину (например, когда атом имеет нечётное число электронов на верхнем уровне), либо когда валентная зона перекрывается с зоной проводимости. Первое характерно, например для Na или Al, а второе – для двухвалентных металлов типа Mg и Ca.

Теорема Блоха.

Зонная теория также основывается на решении стационарного уравнения Шредингера для электронов, движущихся в периодическом потенциале атомов (или атомных остовов) кристаллической решётки, при этом рассматриваются только электроны внешней оболочки атомов, энергия связи которых со своим атомом сравнима с энергией межатомного взаимодействия. Основные допущения данной теории сводятся к тому, что атомы рассматриваются неподвижными и регулярно расположенными в пространстве (т.е. в узлах кристаллической решётки), а взаимодействие электронов друг с другом заменяется некоторым эффективным внешнем полем, т.е. рассматривается так называемое одноэлектронное приближение.

Таким образом, приходим к следующему уравнению:

где - волновая функция электрона,- периодический потенциал, удовлетворяющий условию

где τ – произвольный вектор трансляции кристаллической решётки.

Уравнению (1) удовлетворяет так называемая функция Блоха

где - периодическая функция с периодом, определяемым вектором трансляции кристаллической решётки, т.е.

где - вектор трансляции кристаллической решётки.

Соотношение (3) называют ещё теоремой Блоха (1929). Вектор k называют квазиволновым вектором, который можно представить в виде:

(4)

где p – вектор размерности импульса, который называют квазиимпульсом. Это подразумевает то, что есть определённая аналогия между задачей о движении свободного электрона и движении электрона в периодическом поле. Эта аналогия сводится к тому, что волновая функция свободного электрона

(5)

которая является решением уравнения Шредингера

(6)

где V – объём системы, а волновой вектор иp – импульс электрона, связанный с его энергией обычным соотношением

(7)

Однако для свободного электрона , что означает равновероятное нахождение электрона в любой точке пространства, в то время как для электрона в периодическом поле, т.е. волновая функция должна удовлетворять условию

(8)

что означает, что

(9)

Таким образом, квазиволновой вектор k, фигурирующий в качестве параметра в функции Блоха (3), определяется соотношением (9), из которого следует, что k не является однозначной величиной. Действительно, если вектор k удовлетворяет уравнению (9), то , где- вектор, определяемый соотношением,= ±1, ±2, … . (так называемый вектор трансляции обратной решётки кристалла также удовлетворяет уравнению (9)).

Решение Кронига-Пенни

Периодический прямоугольный потенциал (решение Кронинга-Пенни).

Рис.	Найдём решение уравнения Шредингера для потенциала, показанного на рис. … . Волновая функция имеет вид

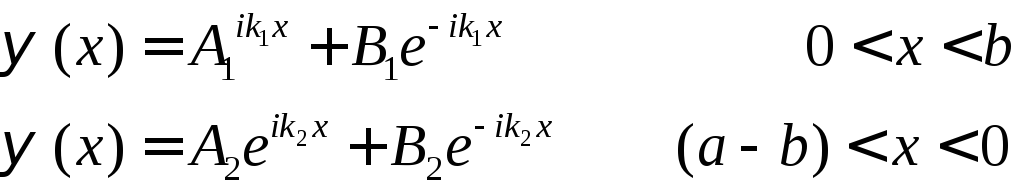
Из условия непрерывности волновой функции и её производной при x=0 получаем

Кроме того, волновая функция должна удовлетворять условию

из которого следует, что значение волновой функции в соответствующих точках, отличающихся на величину, кратную периоду потенциала, может отличаться только фазовым множителем

(*)

Подставляя в (*) соответствующие выражения дляволновых функций в точках и , а также в производную от (x) получим следующие уравнения:

Совместное решение уравнений (*) и (**) приводит к следующему соотношению:

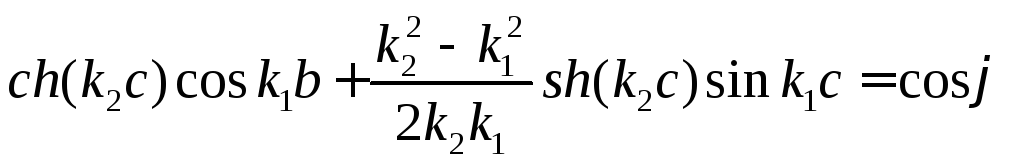
Так как k₁ и k₂ выражаются через E согласно (), то уравнение позволяет в принципе найти спектр значений энергии как функуию произвольного параметра φ. Для более наглядного анализа уравнения () воспользуемся следующим приёмом. Введём величину 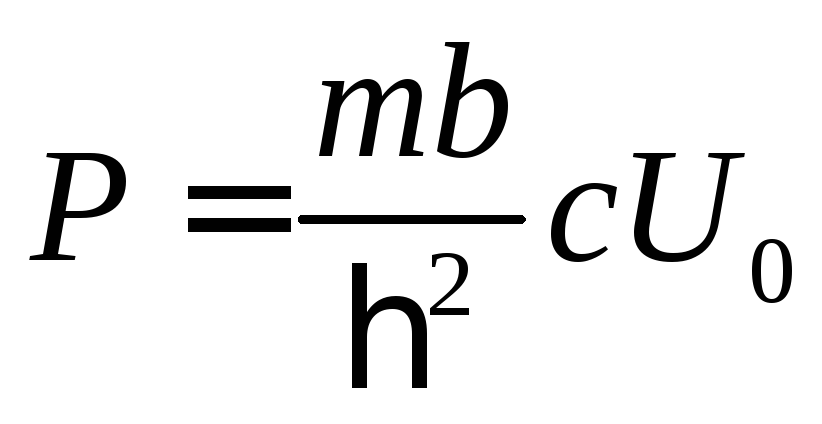,которая характеризует прозрачность барьера, и найдём вид уранения () при с → 0, U₀ → ∞ при условии, что P = const. После этих преобразований приходим к выражению:

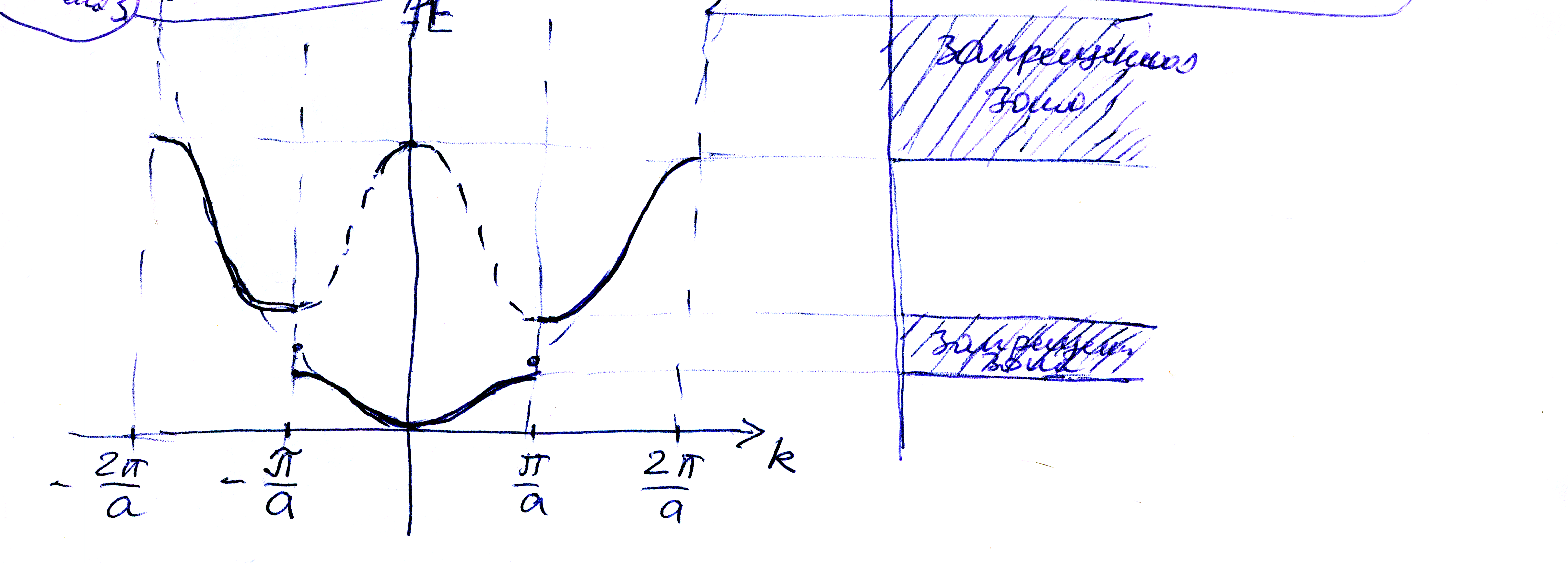
Графическое решение этого уравнения показано на рис.

Градиент вблизи поверхности

х	Вблизи поверхности изменяются плотность, длины связей, упругость связей, ориентация молекул, … , проводимость, коэффициент преломления света и т.д. Поверхностная энергия

Доля поверхности как функция размера