
matan_baza
.pdf
определена только в некоторой окрестности точки M 0 (x0 , y0 ) не определена в точке определена в точке и в некоторой ее окрестности
3.Если функция Z f (x, y) дважды дифференцируема , то
Z |
Z |
|
|
|||||||||||
|
|
xy |
|
|
|
|
|
|
|
yx |
|
|
||
Z |
Z |
|
|
|||||||||||
|
|
xy |
|
|
|
|
|
|
|
yx |
|
|
||
Z |
Z |
|
|
|||||||||||
|
|
xy |
|
|
|
|
|
|
|
yy |
|
|
||
Z |
Z |
|
|
|||||||||||
|
|
xx |
|
|
|
|
|
|
|
yy |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Z |
функции Z x2 x |
y y3 5 равна |
||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
x |
|
|
3y 2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
y |
|
|
||
|
|
|
x |
|
|
3y 2 |
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
||||||||||
2 |
|
|
y |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
|
|
y3 |
3y 2 5 |
|
|
|||||||
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
x2 x 3y 2 |
|
|
||||||||||||
5.Полный дифференциал функции Z f (x, y) определяется по формуле |
||||||||||||||||||||
dZ Z |
Z dxdy |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Z dx |
|
|
|
|
||||||
dZ |
|
|
|
x |
|
|
|
|
|
|
||||||||||
|
Z dy |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||
dZ Z dx Z dy |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
||
dZ Z dx Z dy |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. Z |
|
функции Z x2 |
x |
y y3 |
5 равна |
|||||||||||||||
|
|
|
|
|
|
|
xx |
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y |
|
|
|
|
|
|
||||||||||
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
y |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7. Z |
|
функции Z x2 |
x |
y y3 |
5 равна |
|||||||||||||||
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
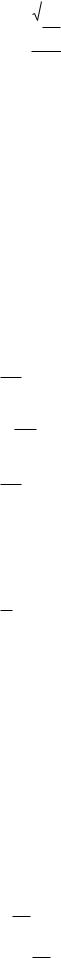
2 |
1 |
|
|
|
|
|
|
|
|
|
|
2 y |
|
||
|
|
||
2x 
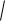 y3
y3
2
8.Полный дифференциал второго порядка функции Z f (x, y) равен
|
|
2 |
|
|
2 |
|
|
|
|
|
|
||
Z xx dx |
|
|
Z yy dy |
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
||
Z xx dx |
|
|
Z yy dy |
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
(Z x dx) |
|
(Z y dy) |
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|||
Z xx dx |
|
|
2Z xy dxdy Z yy dy |
|
|
||||||||
|
|
|
|
|
|
|
|
Z x |
2 |
ny |
|
||
9. Z xy |
|
|
функции |
|
равна |
||||||||
2x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
2x
y
2x y 2
x2
y
10. |
|
2 |
ny равна |
Z xx функции Z x |
|||
2 ln y
1
y ln y
2 ln y
11. Равенство Z Z имеет место для
xy yx
интегрируемой функции Z f (x, y) четной функции Z f (x, y)
любой дважды дифференцируемой функции Z f (x, y) только однородной функции Z f (x, y)
12. Z"xy функции Z y2 ln x равна
1
x2
2 y 1 x2
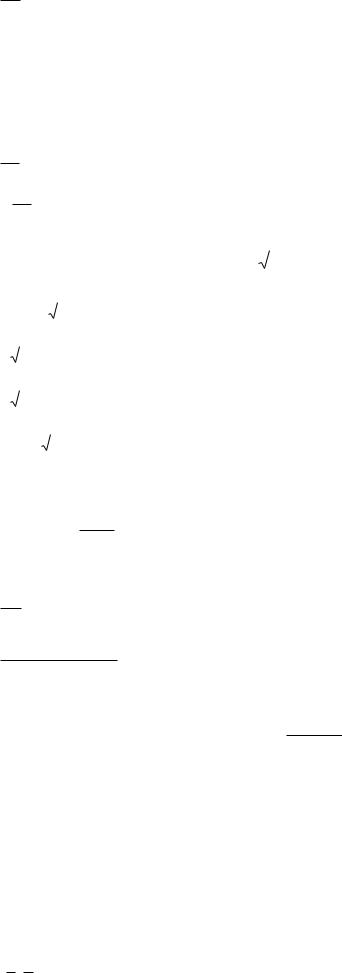
2y
2 y
x
13. Z |
функции Z y2 ln x равна |
|||
|
|
|
xx |
|
y 2 |
|
|
|
|
|
|
y2 |
|
|
|
x2 |
|
||
|
|
|
||
y 2 |
|
|||
x 2
2 y
x2
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|||
14. |
|
|
|
Z xy функции Z x |
y |
x y |
7 |
равна |
||||||||||||
|
|
|
|
|
||||||||||||||||
3x2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 x |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
x |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6x |
|
|
|
y |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
x |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
15. |
|
|
|
Полный дифференциал dz функции Z x2 ln y равен |
||||||||||||||||
2x ln ydx x2dy y
x2dx ln ydy 2yx dxdy
2xy ln ydx x2dy
y
x 2y
16. Градиент функции Z = 2x - y в точке M0 (2;3) определяется
координатами
(8;1) (–15;10) (3;–2) (4;6)
17. Градиент функции Z ln(x2 y2 ) в точке M0 (2;2) определяется координатами
( 12 ; 12 )

(2;2)
(1;1)
(ln4;ln4)
18. |
Градиент функции |
Z = |
1 |
+ |
1 |
в точке M0 (1;1) определяется |
|||
|
|
||||||||
x |
y |
||||||||
координатами |
|
|
|
|
|
||||
(1;1) |
|
|
|
|
|
|
|
||
(2;2) |
|
|
|
|
|
|
|
||
(–1;–1) |
|
|
|
|
|
||||
(– |
1 |
; |
1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
2 |
|
|
|
|
|
|
|
19.Дана функция Z = xe y - x . |grad z| в точке (0;1) равен
1
0 e
e -1
20. Дана функция Z = sin(2x + y). |grad z| в точке ( 4 ; 2 ) равен
0
1

 3
3
2

 5
5
21. Производная функции Z = 
 x2 y 2 по направлению вектора l (4;3) в
x2 y 2 по направлению вектора l (4;3) в
точке M0 (4;3) равна
1
5

 5
5
7
x |
по направлению вектора l (1;1) в |
22. Производная функции Z = y |
точке M0 (–1;1) равна
–1 1

 2
2
1

 2
2
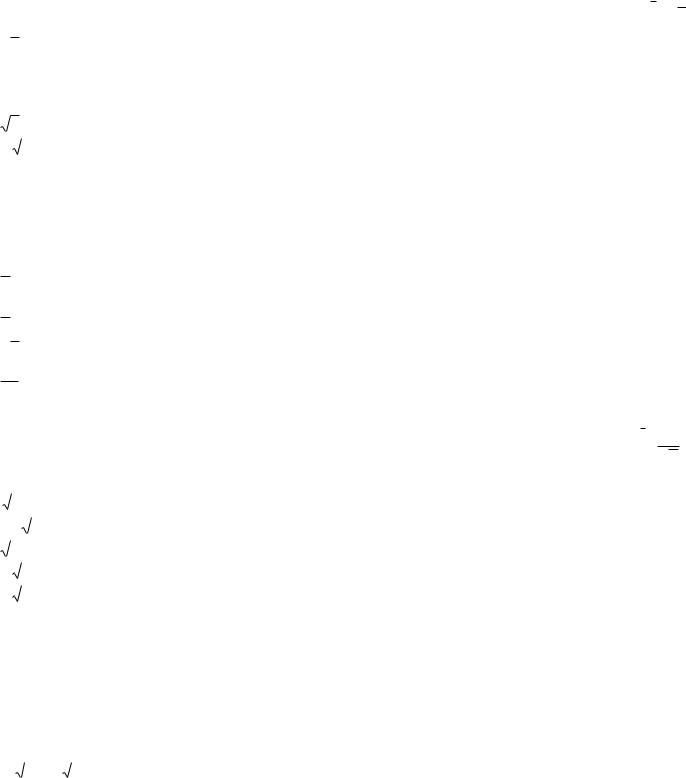
23. Производная функции Z = cos(x – y) по направлению вектора l ( 
 2 ;
2 ;

 2 ) в точке M0 ( 8 ; – 8 ) равна
2 ) в точке M0 ( 8 ; – 8 ) равна
0
1
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
xy |
|
|
|
|
24. Производная функции |
Z = |
по направлению вектора l (6;8) в |
|||||||
|
|||||||||
x y |
|||||||||
точке M0 (2;2) равна
1
4
7
4

 2
2
7
20
25. Производная функции Z = x2 + 4xy по направлению вектора
1 |
|
|
) |
|
|
в точке M0 |
(1; |
1 |
) равна |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
–2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
26. |
|
|
|
Градиент функции Z = |
1 |
в точке M0 |
( |
1 |
; |
1 |
) определяется |
||||||||||||
|
|
|
x y |
2 |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
координатами |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(–4;–4) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(–1;–1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
(–2;–2) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(– |
|
|
2 ; – 2 ) |
|
|
|
|
|
|
|
|
|
|
||||||||||
l ( 1 ;

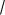 2
2
27.При условиях B2 – 4AC < 0, A > 0 квадратичная форма Ax2 + Bxy + Cy2 является
знаконеопределенной отрицательно определенной неположительно определенной положительно определенной
28.При условии B2 – 4AC > 0 квадратичная форма Ax2 + Bxy + Cy2 является знаконеопределенной
отрицательно определенной неположительно определенной положительно определенной
29.При условиях B2 – 4AC = 0, A < 0 квадратичная форма Ax2 + Bxy + Cy2 является
знаконеопределенной отрицательно определенной неположительно определенной положительно определенной
30.При условиях B2 – 4AC = 0, A > 0 квадратичная форма Ax2 + Bxy + Cy2 является
знаконеопределенной неотрицательно определенной неположительно определенной положительно определенной
31.Квадратичная форма –4x2 – 3xy + 2y2 является знаконеопределенной отрицательно определенной неположительно определенной неотрицательно определенной
32.Квадратичная форма –4x2 + 3xy – 2y2 является знаконеопределенной отрицательно определенной неположительно определенной неотрицательно определенной
33.Квадратичная форма 2x2 – 3xy + y2 является знаконеопределенной отрицательно определенной неотрицательно определенной положительно определенной
34.Квадратичная форма 4x2 – 12xy + 9y2 является знаконеопределенной отрицательно определенной неотрицательно определенной положительно определенной
35.Квадратичная форма –9x2 + 24xy – 16y2 является знаконеопределенной отрицательно определенной неотрицательно определенной неположительно определенной

36. Квадратичная форма x2 – 4xy + 5y2 является знаконеопределенной неположительно определенной неотрицательно определенной положительно определенной
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
37. |
|
|
Z yy функции Z x |
y |
x y |
7 |
равна |
|||||||
|
|
|
|
|||||||||||
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
x 2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6x |
x 2 |
|
|
|
|
|
|
|
||||||
6x |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
x |
|
|
|
|
|
|
|
||||
Тема: 7. Основные теоремы дифференциального исчисления. Применение производной для исследования функций
1.Функция y=f(x) имеет в точке х0 максимум, если
f (x0 ) 0
f (x0 ) 0, f (x0 ) 0
f (x0 ) 0, |
|
f (x0 ) 0 |
|
f (x0 ) 0, |
|
f (x0 ) 0 |
2.Условием выпуклости кривой y=f(x) в интервале ( a , b) является f (x) 0
f (x) 0
f (x) 0 f (x) 0
3.Условием вогнутости кривой y=f(x) в интервале ( a , b) является f (x) 0
f (x) 0 f (x) 0
f (x) 0
4.Функция y f (x) в точке x0 имеет минимум, если
|
|
f (x0 ) 0 , f (x0 ) 0 |
|
|
|
f (x0 ) 0, |
f (x0 ) 0 |
f (x0 ) 0, |
|
f (x0 ) 0 |
|
f (x0 ) 0, f (x0 ) 0
5.Функция f (x) имеет в точке x0 максимум, если для всех x из некоторой окрестности точки x0 выполняется неравенство
f (x0 ) f (x) f (x0 ) 0
f (x0 ) f (x) f (x0 ) 0
6.Функция f (x) имеет в точке x0 минимум, если для всех x из некоторой окрестности точки x0 выполняется неравенство
f (x0 ) f (x) f (x0 ) 0
f (x0 ) 0
f (x0 ) f (x)
7.Если функция y=f(x) во внутренней точке x0 области определения дифференцируема и достигает в точке x0 наибольшего и наименьшего
значения, то производная функции в этой точке f (x0 ) 0
f (x0 ) не существует
f (x0 ) 0 f (x0 )
8.Критическими точками функции f(x) на экстремум, называются точки, в которых для функции f(x) выполняется условие
f (x0 ) 0 f (x0 ) 0 f (x0 ) 0 f (x0 )
9.Если на отрезке a;b для функции f(x) выполняются все условия теоремы Ролля, то на дуге AB найдется точка, в которой касательная к графику проходит через начало координат параллельна оси ординат перпендикулярна оси абсцисс параллельна оси абсцисс
10. Из теоремы Лангранжа следует, что в интервале (a;b) найдется точка c такая, что
f (c) 0 |
|
|
f (b) f (a) |
f (c) |
|
b a |
||
|

|
f (b) f (a) |
|
f (c) |
|
|
|
b a |
|
|
||
|
|
|
|
|
|
|
f (b) f (a) |
|
f (c) |
|
|
|
b a |
|
|
|
|
|
|
|
|
|
|
11. К функциям f(x) и g(x) теорема Коши применима, если |
|||||
f(x) и g(x) |
|
непрерывны на (a;b) |
и дифференцируемы на (a;b) |
||
f(x) и g(x) |
|
непрерывны на |
a;b |
и g (x) 0 в интервале (a;b) |
|
f(x) и g(x) непрерывны на |
a;b , |
дифференцируемы на (a;b) и g (x) 0 в |
|||
интервале (a;b) |
|
|
|||
f(x) и g(x) |
|
непрерывны на (a;b), дифференцируемы на (a;b) и g (x) 0 в |
|||
интервале (a;b)
12. Если функции f(x) и g(x) непрерывны на отрезке a;b , дифференцируемы в (a;b) и g (x) 0 в интервале (a;b), то, согласно теореме Коши, в интервале (a;b) найдется точка с такая, что
f (b) f (a) |
|
f (c) |
||
g(b) g(a) |
|
g (c) |
||
f (b) f (a) |
|
f (c) |
||
g(b) g(a) |
|
g (c) |
||
f (b) f (a) |
|
f (c) |
|
|
g(b) g(a) |
g(c) |
|||
|
||||
f (b) f (a) |
|
g (c) |
||
g(b) g(a) |
|
f (c) |
||
13. Правило Лопиталя применяется к неопределенности вида
0
1
14. Правило Лопиталя применяется к неопределенности вида
0
0
0 1
15. Пусть функции f(x) и g(x) непрерывны в (x0 , a],дифференцируемы в
(x |
, a) , причем g (x) 0 , lim f (x) и lim g(x) ; существует конечный или |
||||
0 |
|
x x0 |
|
x x0 |
|
|
|
|
|||
бесконечный предел |
lim |
|
f (x) |
, то |
|
|
g (x) |
||||
|
|
x x0 |
|
||

lim |
f (x) |
|
lim |
f (x) |
|||||
g(x) |
g (x) |
||||||||
x x |
|
x x |
|||||||
0 |
|
|
|
0 |
|
|
|
|
|
lim |
f (x) |
|
f (x) |
|
|
|
|||
g(x) |
|
g (x) |
|
|
|||||
x x |
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
lim |
|
f (x) |
|
lim |
|
f (x) |
|
||
|
g(x) |
|
g (x) |
||||||
x x |
|
x x |
|||||||
0 |
|
|
|
0 |
|
|
|
|
|
lim |
f (x) |
const |
|
|
|||||
g(x) |
|
|
|||||||
|
|
|
|
|
|
||||
x x |
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
16. Пусть функции f(x) и g(x) непрерывны в (x0 , a],дифференцируемы в
(x |
, a) , причем |
g (x) 0 , lim f (x) 0 |
и lim g(x) 0 ; существует конечный или |
0 |
|
x x0 |
x x0 |
|
|
бесконечный предел
lim |
f (x) |
|
|
lim |
f (x) |
||
g(x) |
g (x) |
||||||
x x |
|
|
x x |
||||
0 |
f (x) |
0 |
|
|
|||
lim |
f (x) |
|
|||||
g(x) |
|
|
g (x) |
|
|
||
x x |
|
|
|
||||
0 |
|
|
|
|
|
|
|
lim f (x) , то x x0 g (x)
lim |
f (x) |
|
c |
|
|
|
|
|
|
|
|
|
|
||||
g(x) |
|
|
|
|
|
|||
x x |
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
lim |
f (x) |
|
lim |
f (x) |
|
|||
|
g (x) |
|||||||
x x |
g(x) |
x x |
||||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||
17. |
Применима ли теорема Ролля к функции f (x) 2 3 (x 1)2 на |
|||||||
отрезке[1;2]
нет, y=f(x) разрывна на отрезке [1;2] да, с=1
нет, y=f(x) не дифференцируема в интервале (1;2)
нет, f (1) f (2)
18. Применима ли теорема Лагранжа к функции f (x) x2 2x 1 на
отрезке [0;2]
нет, функция f(x) разрывна на [0;2] применима
нет, функция f(x) недифференцируема в (0;2)
нет, f (0) f (2)
19. Применима ли теорема Коши к функциям f (x) 2x 3 и g(x) 3  x 1 на отрезке [0;2]
x 1 на отрезке [0;2]
да, c 1615 нет, f (0) f (2)
