32

дает α(1) = 5/16. Тогда

x(2) =[-1/8; 0] T – 5/16 [1/5; 2/5] T = [-3/16; -1/8] T,

что совпадает с решением, полученным в предыдущем примере.

2.3. Решение задачи нахождения условного экстремума

Предыдущий раздел курсовой работы был посвящен изучению методов -ре шения задачи безусловной оптимизации, то есть задачи, в которой не наклады-

вается никаких ограничений на пространство переменных. В инженерной практике такие задачи встречаются чрезвычайно редко, однако рассмотренные выше процедуры используются в качестве инструментария для решения более сложных оптимизационных задач, в которых область поиска ограничена из ка-

ких-либо практических соображений. Существует большое число методов чис-

ленного решения подобных задач, основанных на преобразовании исходной за-

дачи. Ниже будет рассмотрен наиболее распространенный из -нихметод штрафных функций.

2.3.1. Метод штрафных функций

Суть метода заключается в преобразовании исходной целевой функции -по средством включения в нее функции от ограничений, получая таким образом за-

дачу безусловной оптимизации, для решения которой можно использовать рас-

смотренные в первой части методы. Похожее преобразование целевой функции встречается в задачах нелинейного программирования при конструировании функции Лагранжа, однако непосредственно искать экстремум этой функции нельзя, поскольку решение преобразованной задачи находится в узловой точке.

Поэтому переход от задачи условной оптимизации к задаче безусловной опти-

мизации осуществляют посредством включения в целевую функцию''штрафов"

за нарушение ограничений задачи.

Пусть исходная задача имеет следующий вид

min f(x), xÎ RN

при ограничениях

33

gj(x) ≥ 0, j = 1, …, J,

hk(x) = 0, k = 1, …, K.

Тогда преобразованная задача определится выражением

P(x, R) = f(x) + Ω(R, g(x), h(x)),

где Ω - штрафная функция от ограничений задачи, а R - штрафной параметр. На-

личие штрафного параметраR вызвано тем, что введение штрафной функции сильно деформирует поверхность целевой функции, что, в свою очередь, приво-

дит к ухудшению обусловленности преобразованной задачи. Поэтому параметр

R служит "регулятором" веса штрафной составляющей в целевой функции, и

процесс решения задачи разбивается на ряд вспомогательных задач с различны-

ми значениями параметра R и контролем сходимости их решений.

2.3.2. Виды штрафов

Наиболее распространенными видами штрафов являются: квадратичный; ло-

гарифмический; штраф, заданный обратной функцией и штраф типа квадрата срезки. Выбор типа штрафа определяется характером ограничений и порождает,

в свою очередь, проблему удержания рабочей точки внутри области допустимых значений штрафной функции (внутренняя рабочая точка) либо вне ее (внешняя рабочая точка).

Квадратичный штраф

Этот вид штрафа используется для учета ограничений-равенств и имеет вид:

Ω = R{h(x)}2.

Значение штрафа резко возрастает при отклоненииh(х) от нуля. Несмотря на увеличение параметра R, стационарная точка штрафной функцииP(x,R) стремится к х*, так как в пределеh(x(t)) = 0, где t - номер итерации: t = 1, 2, …, Т.

Функция Ω непрерывна и имеет непрерывную производную, откуда следует, что если непрерывны и дифференцируемы f(x) и h(х), то стационарную точку можно найти аналитически.

34

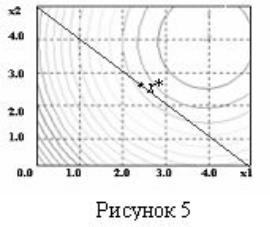
ПРИМЕР 8 Пусть требуется минимизировать

f(x) = (x1 - 4)2 + (x2 - 4)2

при ограничениях

h(x) = x1 + x2 - 5 = 0.

Графически решение задачи представлено на рис.5.

Преобразуем задачу, вводя квадратичный штраф

P(x, R) = (x1 - 4)2 + (x2 - 4)2 + (1/R)( x1 + x2 - 5)2.

Так как f(x) и h(x) просты, то экстремум P(x, R) находим аналитически:

и совместное решение дает

Устремляя R к 0, получим х* = [2.5 2.5]T и f(x*) = 4.5.

Обсудим проблемы численных подходов к решению задачи. Из решения

35

следует, что при вариации R от 0 до достаточно больших значений решение за-

дачи будет изменяться от x1= x2= 10/4= 2.5 до x1=x2=4 (решение задачи без учета ограничений). Таким образом, увеличивая штрафной параметр R, мы уменьшаем

"вес" ограничения в целевой функции Р(х, R). Итак, зафиксировав значение R и

воспользовавшись одной из рассмотренных в первой части процедур численного нахождения экстремума, мы найдем приближенное решение х(0), где верхний ин-

декс означает номер вариации R(0). Выбирая далее R(t) из условия: R(0) > R(1) > R(2) > … > R(t), мы получим приближения х(1), x(2), … , х(t) к х*. Справедлив вопрос, а

нельзя ли сразу принять R = 0 или близкое к нулю значение и найти решение за-

дачи. Во-первых, R выполняет роль весового коэффициента, регулирующего значимость ограничения в составе преобразованной целевой функции. С умень-

шением R стационарная точка функции P(x,R) смещается в сторону более точно-

го выполнения ограниченияh(x)= 0. Во-вторых, с изменением R существенно возрастает крутизна "склонов" поверхности функции вблизи стационарной точ-

ки, что существенно затрудняет работу алгоритмов безусловной оптимизации.

Это и обуславливает итеративность процесса, когда новая итерация начинается из точки, более близкой к точкех* с начальным шагом, не превышающим ко-

нечного значения шага поиска на предыдущее итерации.

Прочие виды штрафов

Рассматриваемые ниже виды штрафов используются, в основном, для огра-

ничений-неравенств g(x).

Логарифмический штраф имеет вид

Ω = -R . ln[g(x)].

Этот штраф положителен для всехх, таких, что 0<g(х)<1, и отрицателен при g(х)>1. Логарифмический штраф - это барьерная функция, не определенная в точках, где g(x)<0. Поэтому на начальном этапе поиска, когда значение шага по-

иска велико, необходимо обеспечить защиту процедуры от попадания рабочей точки в недопустимую область.