UML_4256

Легко проверить, что все три аксиомы определения 1 выполняются, следовательно, пространство действительных чисел метрическое.

Пример 2. Если X = C – множество комплексных чисел, то расстояние введем по той же формуле (1)

Неравенство треугольника следует из геометрических соображений.

Можно проверить, что (2) удовлетворяет определению 1, следовательно, пространство Rn – метрическое.

Пример 4. Если X = C[a,b] – множество непрерывных функций,

соответственно.

В R2 (плоскость, множество С комплексных чисел)

41

a b

непрерывных функций x(t), графики которых не выходят за полосу шириной 2ε , симметричную относительно графика функции x0 (t) (см.

рис.).

Определение 3. Подмножество Е метрического пространства Х

множества Е, содержит и точки множества Х, то точка x0 называется

граничной точкой множества Е.

42

Например, все точки интервала (0,1) R1 внутренние, а точки отрезка [0,1] R1 также все внутренние за исключением точек x = 0 и

x =1. Эти точки граничные.

Замечание. Понятие внутренней и граничной точки множества относительно. Оно зависит от пространства, в которое погружено это

[0,1] R1 не является открытым множеством.

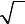
являются изолированными. Точка x0 = 0 является предельной точкой множества А, но не принадлежит этому множеству. Все точки множества B ={1,2, 5} R1 изолированные. Предельных точек это

множество не имеет.

Теорема 2. Если x0 – предельная точка множества E , то любая окрестность точки x0 содержит бесконечное множество точек

множества E .

Доказательство. От противного. Пусть x0 – предельная точка множества E и пусть существует O(x0 ,ε ), содержащая конечное число

множества Е, не совпадающей с x0 . Тогда x0 не является предельной.

Получили противоречие, которое и доказывает нашу теорему. Следствие. Конечное множество не имеет предельных точек.

44

ГЛАВА 2. ПОСЛЕДОВАТЕЛЬНОСТИ

§1. Сходящиеся последовательности в метрическом пространстве. Свойства

Всякое бесконечное пронумерованное множество произвольных элементов мы назовем последовательностью, то есть можно рассматривать последовательность действительных и комплексных чисел, последовательность многочленов и функций, последовательность матриц и прочее.

общий (n-й) член последовательности. Задать последовательность можно, указав вид общего члена последовательности, например,

xn = (−1)n , xn = 1n , xn = n n+1, xn = (x0 + iy0 )2 , xn = sinn t и прочее.

Последовательности {xn } и {yn } равны

def

{xn } = {yn } xn = yn .

Последовательность – это упорядоченное множество. Поэтому следует различать последовательность и множество ее значений. Например, 1, −1,1, −1,1,K и −1,1,1,K разные последовательности, но

множества их значений {−1,1} одинаковы.

Последовательность называют стационарной, если все ее члены, начиная с некоторого, совпадают. Например, −1,2,2,2,... и

cost,sin t,sin t,sin t,.... – стационарные последовательности. Если все члены последовательности совпадают, то последовательность называют постоянной.

Последовательность называют ограниченной, если множество ее

ограниченные последовательности, так как множества их значений

1, 1 , 1 ,... , {−1,1}, {1,sin t,sin2 t,sin3 t,...} – ограниченные.

⎩2 3

Действительно, для первых двух множеств это очевидно, для третьего имеем по определению 3 §14 гл.1

45

ρ(ϕ0 ,ϕn )= sup 1−sinn t ≤ 2.

t R

Последовательность Zn = n2 , очевидно, не ограниченная, так как множество ее значений {1,4,9,...} не ограничено.

Определение 1. Последовательность {xn } точек метрического пространства X называется сходящейся, если существует точка x0 X ,

действительных чисел, то условие сходимости (1) перепишется в виде

что

lim xn = 3, lim ϕn (t )= sin t .

x→∞ x→∞

Докажем теперь некоторые важные свойства сходящихся последовательностей в метрическом пространстве.

46

Теорема. Пусть {xn } – последовательность в метрическом

пространстве Х .

1) Последовательность {xn } сходится к точке x0 X тогда и только тогда, когда любая окрестность точки x0 содержит все члены последовательности {xn }, начиная с некоторого.

2)Если существует предел последовательности {xn }, то он единственный.

3)Если последовательность {xn } сходится, то она ограничена.

4)Если E X и x0 – предельная точка множества Е, то существует последовательность {xn } элементов множества Е, сходящаяся к точке x0 .

{xn } сходится к

точке x0 , то есть

lim xn = x0 . ρ(xn , x0 )< ε n > Nε , ε > 0 – любое.

n→∞

Последнее означает, что xn O(x0 ,ε ) для n > Nε , то есть все члены последовательности {xn }, начиная с n = Nε +1, содержатся в окрестности O(x0 ,ε ). Необходимость доказана.

Пусть теперь наоборот, произвольная окрестность O(x0 ,ε ) содержит все члены последовательности {xn }, начиная с некоторого, то есть

Тогда

Полученное означает, что

lim xn = x0 .

n→∞

Утверждение доказано.

2) От противного. Пусть предел последовательности {xn } не единственный. Например, их два x0 и x0′. Из определения предела следует

Итак, ρ(x0 , x0′ )< ε , то есть расстояние между двумя

фиксированными точками меньше сколь угодно малого числа ε . Это возможно только при x0 = x0′ . Получили противоречие, которое и

выполняться для всех n .

Аэто и означает ограниченность последовательности {xn }.

Утверждение доказано.

4) Пусть x0 – предельная точка множества Е. Согласно

определению предельной точки (см. опр.6 §14 гл.1), любая окрестность точки x0 содержит хотя бы одну точку множества E . Тогда существует

xn такая, что

Теорема доказана.

§2. Сходящаяся последовательность комплексных чисел. Свойства

Чтобы найти предел числовой последовательности {xn } по определению:

следует:

48

1)принять гипотезу, что предел существует и равен x0 ;

2)решить неравенство (1) относительно n для любого ε ;

3)если решение существует и имеет вид n > Nε , то гипотеза верна и предел найден.

Пример 1. Найти предел последовательности xn = n n+1 .

= [−lg ε ]. Что и требовалось доказать.

неограниченная, но не является бесконечно большой.

Если {xn } – последовательность действительных положительных

чисел является бесконечно большой, то в окрестности бесконечно удаленной точки (+∞) (см. §14 гл.1) находятся все члены этой

последовательности, начиная с некоторого. Поэтому пишут

lim xn = +∞ .

n→∞

Аналогично, если последовательность {xn } отрицательных чисел является бесконечно большой, пишут

lim xn = −∞ .

n→∞

Для бесконечно большой последовательности комплексных чисел пишут

lim Zn = ∞.

n→∞

Введем операции над последовательностями. Суммой двух последовательностей {αn } и {βn } назовем последовательность {γn },

общий член которой определим равенством

def

γn = αn + βn .

Аналогично определим разность, произведение и частное этих последовательностей

αn − βn , αn βn , αn , (βn ≠ 0).

βn

Теорема 1. Если последовательности комплексных чисел {αn } и

βn ≠ 0 сходятся. При этом

50