
- •Министерство образования Республики Беларусь
- •I. Решение систем линейных уравнений методом Жордана-Гаусса
- •Матрицы и
- •Решение системы, полученное после приравнивания нулю всех свободных переменных, называется базисным. Алгоритм приведения матрицы к базисному виду
- •Контрольные задания для самостоятельного решения
- •Варианты:
- •II. Решение задачи линейного программирования геометрическим методом
- •Контрольные задания для самостоятельного решения
- •Варианты:
- •III. Решение задачи линейного программирования Симплекс-методом
- •Алгоритм Симплекс-метода
- •Контрольные задания для самостоятельного решения
- •Варианты:
- •IV. Двойственность в линейном программировании. Двойственный симплекс-метод
- •Контрольные задания для самостоятельного решения Задание 4. Решить задачу линейного программирования двойственным симплекс-методом. Варианты
- •V. Транспортная задача
- •Контрольные задания для самостоятельного решения
- •VI. Задача о максимальном потоке в сети
- •Алгоритм расстановки пометок нахождения увеличивающего пути
- •Алгоритм Форда – построения максимального потока в сети.
- •Контрольные задания для самостоятельного решения
- •VII. Сетевое планирование.
- •Алгоритм правильной нумерации.
- •Алгоритм нахождения ранних сроков наступления событий
- •Алгоритм нахождения поздних сроков наступления событий
- •Контрольные задания для самостоятельного решения
- •VIII. Задача о кратчайшем пути
- •Алгоритм построения кратчайших путей в сети
- •Контрольные задания для самостоятельного решения
- •Литература
Контрольные задания для самостоятельного решения
Задание 3. Решить задачу линейного программирования симплекс-методом (x, y 0).
Варианты:
1
 .Z
= x
- 2y
min
2. Z
= -x + y
min
.Z
= x
- 2y
min
2. Z
= -x + y
min
3x + y 8 3x - 2y 7
4x + 5y 29 x + 2y 13
x + 4y 10 x - 2y 1
3. Z = 2x + y max 4. Z = x - y max

 -x
+ 2y
3 -2x + 3y
5
-x
+ 2y
3 -2x + 3y
5
-x + y 1 x + 2y 8
3x - 2y 3 3x - y 10
5. Z = 2x + y max 6. Z = x + y max

 x
- y
0 x - y
0
x
- y
0 x - y
0
3x - 2y 3 -x + 2y 4
5x - 4y 1 -3x + 4y 2
7. Z = 5x + 2y max 8. Z = 2x + 4y max
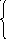
 3x
+ y
9 3x + y
8
3x
+ y
9 3x + y
8
2x + y 7 -x + 3y 4
5x + 2y 17 x + 2y 11
9. Z = 2x + y max 10. Z = x - y min

 -x
+ 5y
4 x + 3y
7
-x
+ 5y
4 x + 3y
7
x - y 4 2x - y 7
x + y 2 5x + y 7
IV. Двойственность в линейном программировании. Двойственный симплекс-метод
Рассмотрим задачу линейного программирования в общей форме:
Z = c1 x1 + c2 x2 + . . .+ cn xn max (1)
при ограничениях :
y10 a11 x1 + a12 x2 + . . .+ a1n xn b1
y20 a21 x1 + a22 x2 + . . .+ a2n xn b2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)
yk0 ak1 x1 + ak2 x2 + . . .+ akn xn bk
yk+1 ak+1 1 x1 + ak+1 2 x2 + . . .+ ak+1 n xn = bk+1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ym am1 x1 + am2 x2 + . . .+ amn xn = bm ,
xj 0 , j = 1, . . . , l; l n (3)
Каждому i-му ограничению из (2) соответствует переменная yi так называемой двойственной задачи к задаче (1) – (3) (показана слева от соответствующего ограничения).
Двойственная задача имеет вид:
W = b1 y1 + b2 y2 + . . .+ bm xm min (4)
при ограничениях :
x1 0 a11 y1 + a21 y2 + . . .+ am1 ym c1
x2 0 a12 y1 + a22 y2 + . . .+ am2 ym c2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (5)
xl 0 a1l y1 + a2l y2 + . . .+ aml ym cl
xl+1 a1 l+1 y1 + a2 l+1 y2 + . . .+ a m l+1 ym = cl+1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
xn a1n y1 + a2n y2 + . . .+ amn ym = cn ,
yi 0 , i = 1, . . . , k ; k n (6)
Задачи (1) – (3) и (4) – (6) образуют пару задач, называемую в линейном программировании двойственной парой.
Сравнивая две задачи, видим, что двойственная задача по отношению к исходной (прямой) содержит те же самые коэффициенты aij, bi, cj и составляется согласно следующим правилам:
Целевая функция (1) исходной задачи задается на максимум, а целевая функция (4) двойственной задачи – на минимум.
Матрица АТ , составленная из коэффициентов при неизвестных в системе ограничений (5) двойственной задачи получается из матрицы А прямой задачи транспонированием (т.е. заменой строк столбцами):


а11 а12 . . . а1n a11 a21 . . . am1
A = а21 а22 . . . а2n AT = a12 a22 . . . am2
. . . . . . . . . . . . . . . . . . . . . . . . .
аm1 аm2 . . . аmn a1n a2n . . . amn
Число переменных в двойственной задаче (4)–(6) равно числу ограничений в системе (2) прямой задачи, а число ограничений в системе (5) двойственной задачи равно числу переменных в прямой задаче.
Коэффициентами при неизвестных в целевой функции (4) двойственной задачи являются свободные члены в системе (2) прямой задачи и наоборот.
Если переменная xj 0, то j-ое ограничение в системе (5) двойственной задачи является неравенством “ ”. Если же переменная xj может иметь любой знак, то j-ое ограничение в системе (5) представляет собой уравнение.
Каждая из задач двойственной пары (1) – (3) и (4) – (6) фактически является самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении симплексным методом оптимального плана одной из задач, тем самым находится решение и другой задачи. Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже теоремами двойственности.
Теорема 1. (Основная теорема двойственности). Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план причем значения целевых функций задач при их оптимальных планах совпадают, т.е. Zmax = Wmin.
Если же целевая функция одной из задач не ограничена (для исходной (1) – (3) – сверху, для двойственной (4) – (6) – снизу), то другая задача вообще не имеет допустимых решений.
Теорема
2. (Вторая
теорема двойственности).
Для того, чтобы два допустимых решения
![]() и
и![]() пары двойственных задач были их
оптимальными решениями, необходимо и
достаточно, чтобы они удовлетворяли
системам уравнений:
пары двойственных задач были их
оптимальными решениями, необходимо и
достаточно, чтобы они удовлетворяли
системам уравнений:
![]()
![]() (7)
(7)
Замечание. Соотношения (7) верны только для ограничений в виде неравенств и для неотрицательных переменных.
Двойственный симплекс-метод, как и симплекс-метод, используется при нахождении решения задачи линейного программирования, записанной в канонической форме. Вместе с тем двойственный симплекс-метод можно применять при решении задачи ЛП, свободные члены системы ограничений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными).
Опишем алгоритм двойственного симплекс-метода. Рассмотрим задачу линейного программирования в канонической форме.
![]() (8)
(8)

 (9)
(9)
![]() (10)
(10)
Пусть
матрица ограничений А
содержит единичную подматрицу порядка
m
и первые m
переменных
![]() являются базисными. Среди чисел
являются базисными. Среди чисел![]() есть отрицательные. Вектор
есть отрицательные. Вектор![]() есть решение системы (9). Однако, это
решение не является планом задачи (8) –
(10), поскольку среди его компонент есть
отрицательные числе (т.е. не выполняются
ограничения (10)). Исключим базисные
переменные из целевой функцииz:
есть решение системы (9). Однако, это
решение не является планом задачи (8) –
(10), поскольку среди его компонент есть
отрицательные числе (т.е. не выполняются
ограничения (10)). Исключим базисные
переменные из целевой функцииz:
![]() .
.
Предположим,
что
![]()
Шаг 1. Составить исходную симплексную таблицу.
|
№ строки |
Базис |
x1 |
… |
xm |
xm+1 |
… |
xk |
… |
xn |
b |
|
1
l
m |
x1
xl
xm |
1
0
0 |
…
…
… |
0
0
1 |
a1m+1
alm+1
amm+1 |
…
…
… |
ak
a*lk
amk |
…
…
… |
a1n
aln
amn |
b1
b
bm |
|
m+1 |
-z |
0 |
… |
0 |
dm+1 |
… |
dk |
… |
dn |
-do |

Шаг 2. Выяснить, имеется ли хотя бы одно отрицательное число среди элементов столбца b. Если нет, то перейти к шагу 8. Иначе – к шагу 3.
Шаг
3. Если
отрицательных чисел в столбце b
несколько,
то выбрать наименьшее. Пусть, для
определенности, это число
![]() .
Строка с номеромl
– ведущая.
.
Строка с номеромl
– ведущая.
Шаг
4. Среди
элементов
![]() ведущей строкиl
находят отрицательные. Если таковых
нет, то исходная задача не имеет решения.
В противном случае перейти к шагу 5.
ведущей строкиl
находят отрицательные. Если таковых
нет, то исходная задача не имеет решения.
В противном случае перейти к шагу 5.
Шаг
5. Вычислить
![]() .
Столбец с номеромk
– ведущий,
.
Столбец с номеромk
– ведущий,
![]() - ведущий элемент.
- ведущий элемент.
Шаг
6. С помощью
ведущего элемента
![]() провести одну итерацию метода
Жордана-Гаусса.
провести одну итерацию метода
Жордана-Гаусса.
Шаг 7. Построить новую симплексную таблицу и перейти к шагу 2.
Шаг 8. Задача линейного программирования (8) – (10) решена. По последней симплексной таблице выписать оптимальный план и минимальное значение целевой функции задачи (8) – (10).
Замечание.
Если среди чисел
![]() есть отрицательные, то следует в системе
ограничений (9) преобразовать свободные
членыbj
в неотрицательные, умножив на (-1)
строки, содержащие отрицательные
свободные члены и решать задачу (8) –
(10) методом искусственного базиса.
есть отрицательные, то следует в системе
ограничений (9) преобразовать свободные
членыbj
в неотрицательные, умножив на (-1)
строки, содержащие отрицательные
свободные члены и решать задачу (8) –
(10) методом искусственного базиса.
Пример. Решить задачу линейного программирования:
Z = 6x1 + 9x2 + 3x3 min
 -x1
+ 2x2
+ x3
2
-x1
+ 2x2
+ x3
2
3x1 + x2 – x3 1 (11)
xj 0, j = 1, 2, 3.
Решение. Составим для задачи (11) двойственную:
W = 2y1 + y2 max
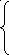 -y1
+ 3y2
6
-y1
+ 3y2
6
2y1 + y2 9 (12)
y1 - y2 3
y1 , y2 0
Для решения задачи (11) двойственным симплекс-методом приведем ее к каноническому виду. Для этого умножим первое и второе ограничения на (-1) и добавим соответственно неотрицательные дополнительные переменные x4 0 , x5 0:
Z = 6x1 + 9x2 + 3x3 min
 x1
- 2x2
- x3
+ x4
= -2
x1
- 2x2
- x3
+ x4
= -2
-3x1 - x2 + x3 + x5 = -1 (13)
xj 0, j = 1, 2, ..., 5.
Базисными переменными здесь являются переменные х4 и х5 . Поскольку все коэффициенты сj 0 , то критерий оптимальности для этого базисного решения выполнен, однако само решение Х = (0, 0, 0, -2, -1) содержит отрицательные переменные, то есть не является допустимым. Естественно попытаться вывести отрицательные (не являющиеся допустимыми) переменные из базиса, сохранив при этом неотрицательность коэффициентов последней строки, так как в этом случае полученное допустимое решение будет являться и оптимальным. Такой подход является содержанием двойственного симплекс-метода. Проиллюстрируем его на примере решения задачи (13).
Составим исходную симплекс-таблицу.
|
Базис |
х1 х2 х3 х4 х5 |
Значение (bi) |
|
x4 x5 |
1 -2 -1* 1 0 -3 -1 1 0 1 |
-2 -1 |
|
- Z |
6 9 3 0 0 |
0 |
Вычисляем
 Из базиса будем выводить переменнуюx4.
Следовательно, первая строка таблицы
является разрешающей. Среди элементов
разрешающей строки находим отрицательные
а12
= -2; a13
= -1.
Из базиса будем выводить переменнуюx4.
Следовательно, первая строка таблицы
является разрешающей. Среди элементов
разрешающей строки находим отрицательные
а12
= -2; a13
= -1.
Определяем
![]() Столбец, в котором достигается этот
минимум, соответствует переменнойх3.
Этот столбец является разрешающим и
разрешающим элементом является элемент
а13
= -1. Это делается для того, чтобы элементы
последней строки остались неотрицательными.
Проводим одну итерацию метода
Жордана-Гаусса относительно этого
элемента, т.е. из базиса исключаем
переменную х4
и включаем в базис переменную х3.
Новая симплекс-таблица имеет вид:
Столбец, в котором достигается этот
минимум, соответствует переменнойх3.
Этот столбец является разрешающим и
разрешающим элементом является элемент
а13
= -1. Это делается для того, чтобы элементы
последней строки остались неотрицательными.
Проводим одну итерацию метода
Жордана-Гаусса относительно этого
элемента, т.е. из базиса исключаем
переменную х4
и включаем в базис переменную х3.
Новая симплекс-таблица имеет вид:
-
Базис
х1 х2 х3 х4 х5
Значение
(bi)
х3
x5
-1 2 1 -1 0
-2 -3* 0 1 1
2
-3
- Z
9 3 0 3 0
-6
Элемент
b2
= -3 < 0. Следовательно, разрешающей
является вторая строка таблицы. Как и
ранее, находим
![]()
Следовательно второй столбец – разрешающий, переменную х2 включаем в базис, переменную х5 исключаем из базиса. Пересчитывая таблицу относительно элемента а22 = -3, получаем новую таблицу:
-
Базис
х1 х2 х3 х4 х5
Значение (bi)
х3
x2
-7/3 0 1 -1/3 2/3
2/3 1 0 -1/3 -1/3
0
1
- Z
7 0 0 4 1
-9
Среди элементов столбца “Значение” нет отрицательных чисел. В Z – строке также нет отрицательных чисел. Следовательно, найден оптимальный план: Х* = (0; 1; 0), при этом Z* = Zmin = 9. По последней симплекс-таблице находим решение двойственной задачи (9). Для этого выясняем, какие переменные задачи (10) входили в исходный базис. В первоначальной таблице это – х4, х5. В последней симплекс-таблице находим элементы Z – строки, соответствующие этим базисным переменным (с4 = 4, с5 = 1) и прибавляем к ним соответствующие коэффициенты исходной целевой функции (с4 = с5 = 0). В результате получаем Y* = (4; 1), W* = Wmax = 9.

 l
l