РТЦС-методичка

--41--

Раздел 6. Дискретизация сигналов с ограниченным спектром

6.1. Краткое теоретическое введение

Теоретической основой дискретизации сигналов служит теорема Котельникова. В зависимости от размещения дискретизируемых сигналов на оси частот и их энергетических характеристик используют различные варианты формулировки теоремы Котельникова.

Теорема Котельникова для импульсов с ограниченной энергией утверждает, что сигнал, описываемый непрерывной, интегрируемой с квадратом функцией s(t) спектр которой огра-

ничен частотой Fм, полностью и однозначно определяется последовательностью своих мгновенных значений, считываемых с частотой дискретизации

Данное утверждение основано на том факте, что замена континуального сигнала s(t) дискретизированным

k -

где T = 1 / F - интервал дискретизации сигнала, вызывает периодическое по частоте повторение спектральной плотности исходного сигнала [1, с. 65-66; 2, с. 71-72; 3, с. 377]

n -

При выполнении условия (6.1.1) перекрытия спектральных полос при дискретизации не происходит, и спектральная плотность принимает вид, показанный на рис. 18. Из полученной структуры спектральной плотности следует, что

1) Любой фильтр, обладающий равномерным коэффициен-

том передачи в полосе частот от 0 до Fм и полностью по-

--42--

давляющий спектральные составляющие в полосе | f | > (F - Fм) позволяет без искажения выделить из спектральной плотности дискретизированного сигнала все составляющие относящиеся к исходному (и только исходному) сигналу, а значит без искажений восстановить сигнал по его дискретным отсчетам. В частности, для восстановления сигнала можно применить идеальный фильтр низких частот с частотой среза FM FC ( F - FM ); при этом сигнал на выходе фильтра определится соотношением

k

где sinc( x ) = sin( x ) / x.

2) Если используемый фильтр имеет граничную частоту FC > FM , то минимально допустимая частота дискретизации увеличивается и должна выбираться из условия

Рис. 18. Спектральная плотность дискретизированного сигнала

Формулировка теоремы Котельникова для импульсов с неограниченной энергией, но конечной мощностью требует изменить неравенства в соотношениях (6.1.1) и (6.1.5) на стро-

--43--

гие, т.е. совпадение частоты дискретизации с удвоенной максимальной частотой спектра сигнала становится недопустимым:

Другие формулировки теоремы Котельникова, ориентированные, в частности, на работу с радиосигналами, можно най-

ти, например, в [4, с. 50-55].

6.2. Типовые задачи

Задача 1. Какой из интервалов дискретизации Т1 = 20 мкс, Т2 = 12,5 мкс, Т3 = 10 мкс или Т4 = 5 мкс разумнее всего применить для дискретизации колебания

s(t) = S0 · ( 1 + 0,4·cos( 4π103·t + 45˚ ) ) · cos( 7,6π104·t - 30˚ ),

чтобы используя идеальный фильтр низких частот (ИФНЧ) по полученным отсчетам можно было без погрешности восстановить это колебание? В каких пределах при выбранном интервале дискретизации можно изменять частоту среза восстанавливающего фильтра?

Решение

а) Анализ большинства задач, связанных с применением теоремы Котельникова, полезно начинать с построения двухстороннего комплексного спектра дискретизируемого сигнала. Для указанного в условии амплитудно-модулированного колебания такой спектр показан на рис. 19.

б) Наиболее высокочастотная спектральная составляющая сигнала расположена на частоте FМ = 40 кГц. Поскольку сигнал s(t) периодический, то частоту дискретизации следует выбирать по правилу (6.1.6). Как следствие, интервал дискретизации должен удовлетворять соотношению T = 1 / F < 12,5 мкс, поэтому первые два из предложенных в условии значений T использовать нельзя.

--44--

Sn

S0

0,2·S0

Рис. 19.

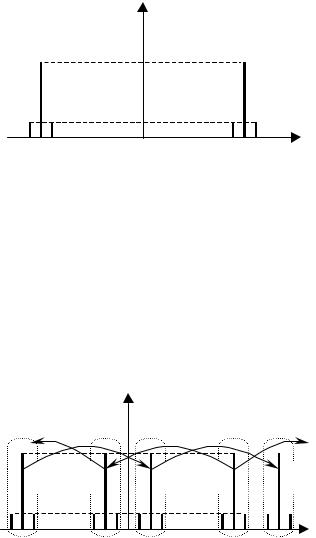
Для пояснения причин недопустимости использовании при дискретизации интервала T = T1 на рис. 20 показан результат периодического повторения спектра исходного сигнала с периодом по частоте F = 1 / T = 50 кГц. При первом же смещении на интервал F вправо группа спектральных составляющих исходного сигнала с отрицательными частотами (обозначенная на рис. 20 как "Л0") попадает в полосу 10…14 кГц (см. пометку "Л+1" на рис. 20). Таким образом, оказывается невозможным (каким бы то ни было) фильтром низких частот выделить

Рис. 20. Спектр дискретизированного сигнала при F < 2 · Fм

спектральные составляющие исходного сигнала, не захватывая при этом (и не пропуская на выход) дополнительно обра-

--45--

зовавшиеся в результате дискретизации гармоники, а значит неизбежно существенное искажение формы сигнала.

При Т = Т2, как показано на рис. 21, ситуация заметно улучшается. При повторении спектра с периодичностью F2 = = 1 / T2 = 80 кГц спектральные составляющие "Л0" переносится в область частот f ≥ 40 кГц, однако составляющая с частотой f = 40 кГц имеет иную амплитуду чем в исходном сигнале. Если применительно к сигналам с ограниченной энергией, т.е. обладающим сплошным спектром с бесконечно малыми амплитудами гармоник, потеря или искажение одной составляющей спектра влечет бесконечно малую (и, следовательно, незаметную практически) корректировку сигнала, то применительно к дискретному спектру, где каждая спектральная составляющая обладает некоторой ненулевой мощностью, такие потери недопустимы (приводят к заметному изменению формы сигнала). Поэтому как пропуская на выход, так и отфильтровывая идеальным фильтром гармонику с частотой f = 40 кГц в случае, показанном на рис. 21, избежать искажений нельзя.

Предложенные в условии значения Т3 = 10 мкс и Т4 = 5 мкс оба являются допустимыми, однако, при выборе T = T4 сиг-

--46--

зования для восстановления сигнала по его отсчетам реального фильтра вместо ИФНЧ, когда увеличение частоты дискретизации помогает уменьшать погрешность).

в) Полоса пропускания восстанавливающего фильтра должна быть такой, чтобы пропускать все гармоники полезного сигнала и подавлять побочные продукты дискретизации, поэтому при рекомендуемой частоте дискретизации F = 1 / T3 = 100 кГц частоту среза ИФНЧ следует выбирать из условия

40 < Fс < 80 кГц.

Задача 2. В результате дискретизации и последующего восстановления идеальным фильтром низких частот (ИФНЧ) сигнала s1(t), показанного на рис. 22, был получен сигнал s2(t), представленный на рис. 23. Определить использованную частоту дискретизации F и параметры восстанавливающего фильтра. Можно ли улучшить форму восстанавливаемого сигнала, не изменяя частоту дискретизации?

Решение

а) Из выражения (6.1.4) видно, что сигнал на выходе восстанавливающего фильтра представляет собой сумму задержанных по времени на интервал T и взвешенных (усиленных) с коэффициентами s1(kT) импульсных характеристик gИФНЧ(t) идеального фильтра. Форма сигнала s2(t), показанного на рис.

--47-- 23, однозначно указывает на то, воздействующие на вход фильт-

ра импульсы поступают недостаточно часто, так что создаваемые ими отклики практически не перекрываются. В соответствии с интервалами между основными всплесками, наблюдаемыми на рис. 23, частота дискретизации составляет

F = 1 = 4 / τ .

4

б) Интервал между соседними нулями импульсной характерис-

тики gИФНЧ(t) = 2·K0·Fc·sinc(2π·Fc·t) равен t0 = 1 / 2Fc, а из

K0 = 1 / 2·Fс·T = 1 / 12 .

г) Итак, в анализируемом случае сигнал, представленный на рис. 22, дискретизируется с частотой F = 4 / τ и затем восста-

навливается фильтром, имеющим частоту среза Fс = 24 / τ ,

таким образом наблюдается соотношение Fc = 6 · F, что находится в явном противоречии с требованиями теоремы Котельникова. Исследуя спектр исходного сигнала, можно убедиться, что для снижения погрешности выгоднее всего значительно повысить частоту дискретизации, но если выполнить это невозможно то, по крайней мере, следует привести в соответст-

вие друг с другом F и Fc. В данном случае для этого следует

взять частоту среза ИФНЧ в 12 раз ниже, а именно Fс = 2 / τ . Поскольку спектр дискретизируемого сигнала весьма широк (формально, неограничен), то нулевой погрешности добиться таким образом невозможно, но форма получаемого сигнала станет все же гораздо ближе к исходной. Приближенный вид получаемого в результате сигнала показан на рис. 24.

--48--

S3(t)

Рис. 24. Восстановленный сигнал при уменьшенной в 12 раз частоте среза восстанавливающего фильтра

Для более полного усвоения учебного материала разберите также решения задач 2.39-2.41, приведенные в задачнике [5,

с. 28-29].

Задача контрольной работы (№6):

По заданномуаналитическомувыражению колебания

определить можно ли представить это колебание последовательностью дискретных отсчетов и затем восстановить с пренебрежимо малой погрешностью, используя в качестве восстанавливающего идеальный фильтр низких частот с час-

тотой среза Fc = 12 кГц?

В случае положительного ответа

указать диапазон допустимых значений частоты дискретизации F.

Подлежащие дискретизации напряжения (в вольтах) приведены в таблице ниже

13 · cos( 6 103t ) · sin( 8 103t )

2sin( 2 104t ) + cos( 4 103t )

Раздел 7. Анализ дискретного (цифрового) фильтра на основе его импульсной характеристики

7.1. Краткое теоретическое введение

Дискретным фильтром называют линейное устройство предназначенное для обработки дискретных сигналов (последовательностей дискретных отсчетов) функционирующее в соответствии с правилом

где s1(k) - отсчеты входного, s2(k) - отсчеты выходного сигна-

ла, а константы ar и bm - коэффициенты прямой и обратной передачи сигнала в ветвях фильтра (индексы r и m обозначают число тактов, на которые задерживаются соответственно входной и выходной сигналы до воздействия на данную ветвь).

Графически такое устройство принято отображать структурной схемой, показанной на рис. 25, где треугольники - это

--50--

масштабирующие устройства, блоки с пометкой "T" - устройства задержки сигналов на один такт, а элемент со значком "+" - многовходовой сумматор.

Рис. 25. Структурная схема дискретного фильтра

Как уравнение (7.1.1), так и структурная схема, показанная на рис. 25, однозначно определяют свойства фильтра, однако более универсальными способами описания фильтра являются его импульсная и частотная характеристики.

Импульсной характеристикой дискретного фильтра называют безразмерную последовательностью чисел g(r), соответствующую реакции этого фильтра на единичный отсчет, воздействующий на вход фильтра в начальный момент времени. Из линейности фильтра следует, что его реакция на произвольную входную последовательность отсчетов s1(k) равна

r

Выражение (7.1.2) является дискретным аналогом интеграла Дюамеля и называется дискретной сверткой функций g(r) и s1(k).

Из принципа причинности, утверждающего, что реакция не может опережать воздействие, следует, что импульсная характеристика любого реализуемого фильтра удовлетворяет соотношению g(r) ≡ 0 при r < 0, поэтому при расчете реакции на